Inscription / Connexion Nouveau Sujet
Détermination d'un angle avec la verticale
Bonjour,
Je suis élève en terminale et je bloque sur un exo de mécanique. Voici l'énoncé :
Un pendentif est suspendu au rétroviseur d'une voiture.On le modélisera par un objet ponctuel de masse m = 5,0 g accroché à un fil de longueur l= 10 cm.
1. Déterminer l'angle entre la verticale et le pendentif si la
voiture a les mouvements rectilignes horizontaux suivants.
a. Accélération de 0 à 100 km/h en 12 s.
b.Arrêt en 100 m en étant lancée à 100 km/h
Les accélérations seront supposées constantes. Toute action de l'air sera négligée. La démarche devra être détaillée dans les deux cas.
2.Répondre à la même question si la voiture parcourt, à 70 km·h−1,
un virage horizontal circulaire de rayon
R = 100 m. On utilisera le repère de Frenet.
Tout d'abord j'ai désirer calculer l'accélération dans la situation 1a , 1b et 2.
Pour la question 2 l'accélération vaut uniquement V²/R car nous sommes dans le cas d'un mouvement circulaire uniforme.
Pour la 1a j'ai utilisé le fait que nous sommes en MRUA donc que v étant la primitive de l'accélération par rapport au temps j'ai obtenu : V= a×t +v0 ce qui me permet de conclure que a≈2.3 m/s²
Enfin pour la 1b j'ai utilisée la même formule que pour la 1a mais en utilisant aussi le fait que la position c'était la primitive de la vitesse par rapport au temps ce qui donne que x= 1/2×at²+t×v0+x0
Ce qui me donne après résolution de ce système d'équations une accélération d'environ -3.9 m/s².
Et pour déterminer l'angle que je vais appeler thêta je suis complètement bloqué car quand je m'imagine la situation le pendentif étant un système pseudo-isolé , quand la voiture accélère il est "projeter vers l'arrière" donc j'ai l'impression que le référentiel n'est pas galiléen et du coup je pourrais pas trop appliquer le PFD.
Merci d'avance pour vos éclaircissements
Bonjour,
Question 1 :
Le plus simple est d'utiliser un référentiel terrestre dans lequel tu pourras appliquer le PFD
Ensuite ( et comme d'habitude ) faire la liste des forces appliquées, faire un schéma, choisir un repère et appliquer le PFD
Ha bah enfaite c'est ce que j'avais fais au tout début c'est juste que le raisonnement me paraissait bizarre.
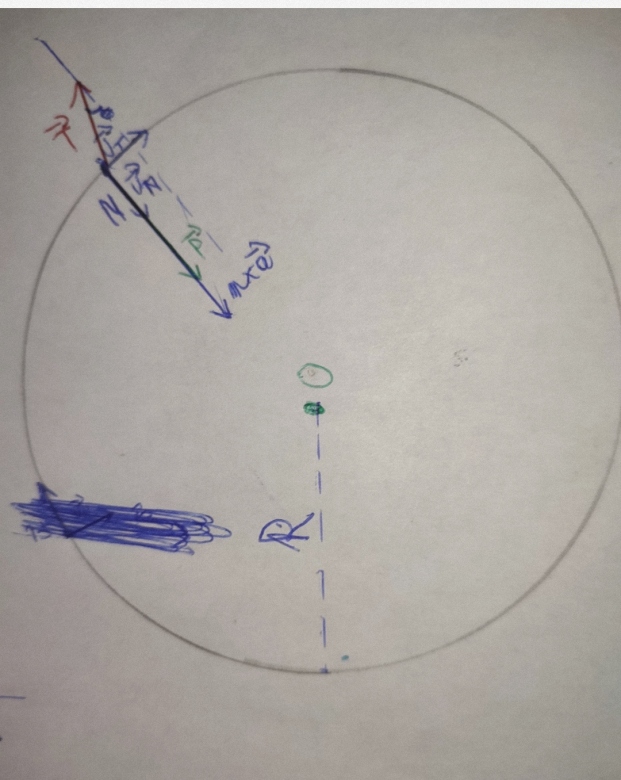
Du coup en faisant ça pour là a étant donné que mon pendentif est soumis à la force de Tension T qui , pour la cas d'une accélération, pas vertical et vers haut mais incliné vers le sens du mouvement et vers le haut
et à son poids qui est lui vertical vers le bas
Le vecteur m×a est du coup dans le sens du mouvement.
Donc en projetant sur Ox et Oy j'ai obtenu le système suivant :
T×sin(thêta) +0= m×a
T×cos(thêta)-m×g=0
En simplifiant ce système j'obtiens qu'il est équivalent à :
thêta = arctan(a/g)
T=mg/cos(thêta)
En supposant que thêta est différent de 90°
J'obtiens en fais l'application numérique pour la 1a que thêta ≈13.2° et que thêta≈21.7° en appliquant le même raisonnement mais pour la question 1b.
En espérant que le raisonnement (vu que j'ai pas utiliser la longueur du fil) j'arrive à ces résultats.
Mais pour la question 2 je me trouve bloqué par le fait que je n'arrive vraiment pas à me représenter mon système et à mettre les vecteur P et T et mon angle thêta dans mon schéma de principe en utilisant le repère de Frenet.
Question 1 :
C'est bon !
En prenant g=9,8 m/s² et en évitant les arrondis dans les calculs intermédiaires j'ai obtenu pour l'angle θ les valeurs de 13,3° et 21,4°
Question 2 : Le repère de Frenet est centré sur le système étudié. Ses vecteurs unitaires sont l'un noté tangent à la trajectoire (et de même sens que le mouvement ) ; l'autre noté
perpendiculaire à
et tourné vers l'intérieur de la trajectoire.
Les vecteurs poids et tension du fil ont leurs directions et sens habituels.
Le PFD s'applique :
Lorsque le mouvement est circulaire uniforme de vitesse V et de rayon R le vecteur accélération est centripète ( même direction et même sens que
) et son module est égal à V²/R
Parfait , la question 1 la démarche était bonne au final, merciii.
Pour la question 2 enfaite j'ai utilisé justement le repère de frenet et je suis arrivé "en me mettant à la place du pendentif" que mon vecteur P est colinéaires est de même sens que mon vecteur tangentielle .
Et pour mon vecteur T il était de même sens que le mouvement mais vers " haut à droite".
Enfaite c'est la même situation que mon tout premier schéma.
J'obtiens finalement ce schéma de principe :
Mais j'ai des sérieux doute quand au placement de mon vecteur P car normalement je devrais en ajoutant mon vecteur T et P tomber sur le vecteur m×a plus ou moins ce qui n'est pas le cas dans ce schéma.
J'aimerais donc savoir comment bien placer mes vecteurs dans le référentiel de frenet sur le schéma de principe
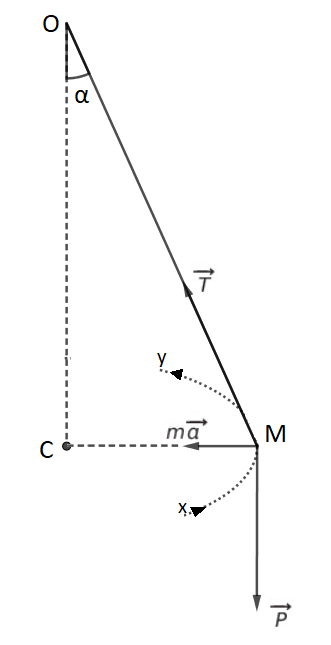
Voir mon schéma :
x ...... y : Trajectoire circulaire de l'objet ponctuel
O : Point de suspension du fil
M : Objet ponctuel
C : Centre de la trajectoire
CM = R : Rayon de la trajectoire
α : Angle à calculer
PFD :
Par souci de clarté je n'ai pas représenté les vecteurs unitaires.
Ha voilà là c'est parfait.
Donc en projetant sur l'axe Un et Ut ça me donne le système d'équations suivant :
Ce qui équivaut , avec au système :
Ce qui fais après application numérique :
alpha≈21,1°
Donc enfaite dans cette exo on a même pas eu besoin de l'informatique sur la longueur du fil c'était un piège du coup.
En effet, les données concernant la longueur du fil ainsi que la masse de l'objet ponctuel étaient superflues.