Bonsoir,

Merci de poser des questions précises à la place du trop souvent entendu " Je n'y arrive pas "
Les topics sur l'or ont été nombreux ces derniers temps. Lequel (lesquels) as tu consulté ?

J'ai cherché toute la journée sur tout un tas de site, j'ai pu voir sur le topic de SweeneyTodD17 par exemple où il y avait presque la même question  " Démontrer que le rayon atomique de l'or est r = 1,4.1010m " vous avez répondu par :
" Masse volumique de l'or : = 4m / a³          
Géométrie de la maille : a =  \dfrac{4r}{ \sqrt{2} }
On a 2 relations et deux inconnues.
On en retire :

r= \sqrt[3]{ \dfrac{  \sqrt{2}~m }{8 \rho } }
AN : r = 1,4.10-10 m = 140 pm

a =  \sqrt[3]{ \dfrac{4m}{ \rho } }
AN : a = 4,1.10-10 m = 410 pm  "
Mais je n'est pas compris d'où sortent les deux relations.

Sur le site "Kartable" j'ai vu que : 4 x R = a x racinecarré de 2
donc R = a x racinecarré de 2 / 4  c'est peut être ça ?
C'est la première fois que je demande de l'aide mais la j'étais obligée notre professeur nous a mis la moitié du cour sur internet et il fallait que l'on comprenne. Je vous remercie d'être patient(e).

Ah j'ai fais copier coller et ça n'a pas écrit les bonnes choses donc je réécris, vous avez répondu " Masse volumique de l'or : = 4m / a³         Géométrie de la maille : a =  4r /2
On a 2 relations et deux inconnues.
On en retire :

r= 32m / 8 ( la racine enveloppe 2m/8p )
AN : r = 1,4.10-10 m = 140 pm

a = 34m / ( la racine enveloppe 4m/p )
AN : a = 4,1.10-10 m = 410 pm "


***Edit gbm : le plus simple la prochaine fois est de faire un raccourci vers le topic en question : Des édifices ordonnés : Les cristaux ***

Relation ρ = 4m/a³
La masse volumique ρ est le rapport entre la masse totale de la maille et le volume de cette maille.
Dans le système "cfc" chaque maille renferme 4 atomes d'or de masse " m "
Masse totale de la maille : 4m
Volume de la maille : a³
ρ = 4m/a³

----------------------------------------

Relation a =
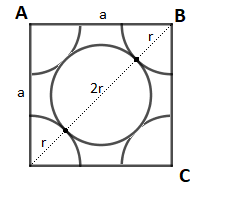
Il faut connaître la disposition des atomes dans le système cfc ( voir figure )
En appliquant le théorème de Pythagore AB² + AC² = BC²
AB = BC = a
BC = r + 2r + r = 4r
a² + a² = (4r)²
2a² = 16r²
a² = 8r²
a = 2*2*r = 4r / 2

Désolé :
Pythagore :
C'est évidemment AB² + BC² = AC²
Cela ne change en rien le reste du calcul