Inscription / Connexion Nouveau Sujet
Démonstration norme de l'accélération
Bonsoir,
Je cherche à démontrer que a = g.sin(Θ)
Je sais comment faire :
Résultante = m.a (2e loi de Newton)
(=) a = Résultante / m
(=) a = m.g.sin(Θ) / m
(=) a = g.sin(Θ)
Ce qui me pose problème c'est qu'à la ligne trois je ne sais d'où vient l'égalité Résultante = m.g.sin(Θ)
Je ne sais pas si elle est admise ou bien si j'ai besoin de la démontrer et si c'est le cas je ne sais pas comment.
Pouvez vous m'aider ?
Merci d'avance
Encore une fois, je ne peux pas t'aider si tu ne nous décris pas en détails la situation, avec un schéma par exemple.
Parce que ce "g.sin(
)" dépend aussi du choix du repère ...
Un mobile descend sur un plan incliné Θ.
On vient de démontrer la 2eme loi de Newton et on me demande maintenant de démontrer que a = g.sin(Θ)
Bon, je pense qu'il faut que tu revois comment introduire un exercice de mécanique (qui commence toujours de la même façon).
Pour cela, je te conseille de lire attentivement cette fiche nouvellement publiée pour que tu puisse comprendre l'intérêt de définir son système, le référentiel d'étude, la nécessité de faire un bilan des forces et de définir un repère d'étude : 
Statique et dynamique - Les lois de Newton
A noter que la réponse à ta question se trouve dans une application, deuxième intérêt de cette fiche 
.
A disposition si nécessaire à l'issue de ta lecture assidue.
J'ai trouvé dans la fiche le schéma qui correspond à ma situation.
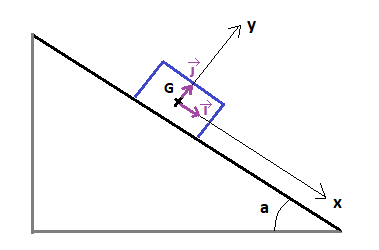
Le système étudié est de masse m et de centre d'inertie G.
Le référentiel d'étude est le référentiel terrestre supposé galiléen et muni du repère cartésien (G,x,y).
Bilan des forces :
- Le poids P :
- point d'application : G
- direction : verticale
- sens : vers le bas (centre de la Terre)
- La réaction normale RN :
- point d'application : point de contact mobile/plan
- direction : oblique
- sens : perpendiculaire au plan, vers le haut
Les frottements sont négligés.
On a la relation : somme des forces extérieures = m.a
Le vecteur a est constant au cours du mouvement.
Il faut maintenant démontrer que l'accélération subie par le mobile vers le bas de la pente correspond à :
a = g.sin(theta)
Bonjour polari56,
Aussi bien présenté, ta demande est beaucoup plus claire, tu ne trouves pas ?
Tu peux donc représenter les forces appliquées au système sur le schéma , écrire la relation vectorielle exprimant la deuxième loi de Newton et la projeter suivant l'axe (Gx).
Tu retrouveras la relation escomptée.
Annuler
connectez vous