Inscription / Connexion Nouveau Sujet
Décharge d'un condensateur
Bonjour
Dans le circuit ci dessous (cas de la charge du condensateur) et apres un temps suffisamment long quelle peut etre l'expression de Q0
Et quelle peut être l'expression de l'énergie électrique emmagasinée du condensateur C1
Merci pour votre aide précieuse
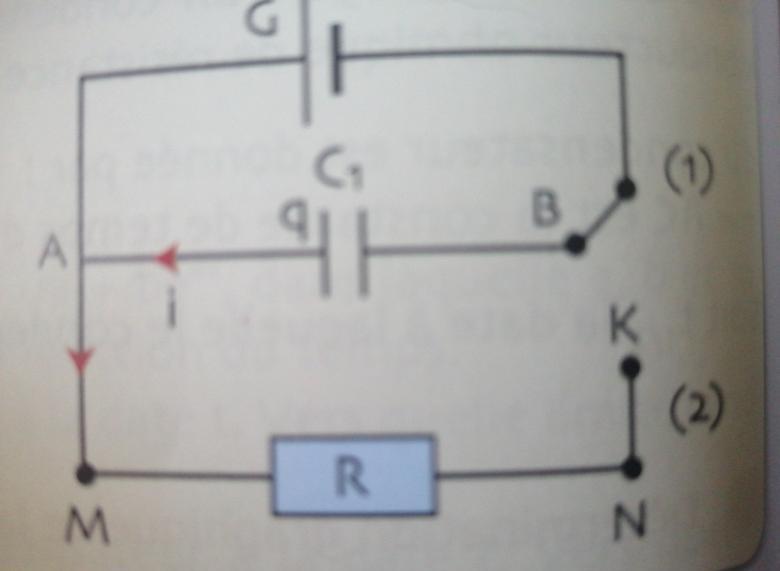
Bonjour,
Quelle est la relation entre la charge d'un condensateur et la tension à ses bornes ?
Le condensateur étant monté en parallèle avec le générateur, quelle est la tension aux bornes du condensateur ?
Quelle est l'expression de l'énergie d'un condensateur ?
Le condensateur étant monté en parallèle avec le générateur, quelle est la tension aux bornes du condensateur ?
Quelle est l'expression de l'énergie d'un condensateur ?
ug= E
Et l'expression de l'énergie est Eel =1/2 C*Uc2
Oui d'après la loi dadditivite des tensions Ug+Uc=0?
Comment je cherche Q0 apres un temps suffisamment long
D'après votre expression : Q=C E (j'ai rectifié le signe en prenant en compte la position de q sur le schéma et le branchement du générateur).
Donc Q est une constante, après "un temps suffisamment long", cette constante sera égale à elle-même.
Il pourrait y avoir des problèmes temporels si votre schéma était différent : en série (générateur, condensateur, résistance, interrupteur)
D'accord donc comme résultat
Après un temps suffisamment long Q0=C*E
Et Énergie =1/2*C*Uc =1/2*C*E=Q/2
C'est ça ?
Bonjour,
Votre formule initiale de l'énergie était correcte (à 08:59), là il y a un 2 qui est passé à la trappe.
Bonjour
Comment je peux demontrer cette relation ? q'=Q0-q
Sachange de Q0 c'est la charge initialle de C1
q charge de C1 et q' charge de C2
Voilà le graphe
Ya til une relation qui démontre que q'=q? Pour arriver a cette relation ou bien ya t il autre méthode ?
Merci d'avance
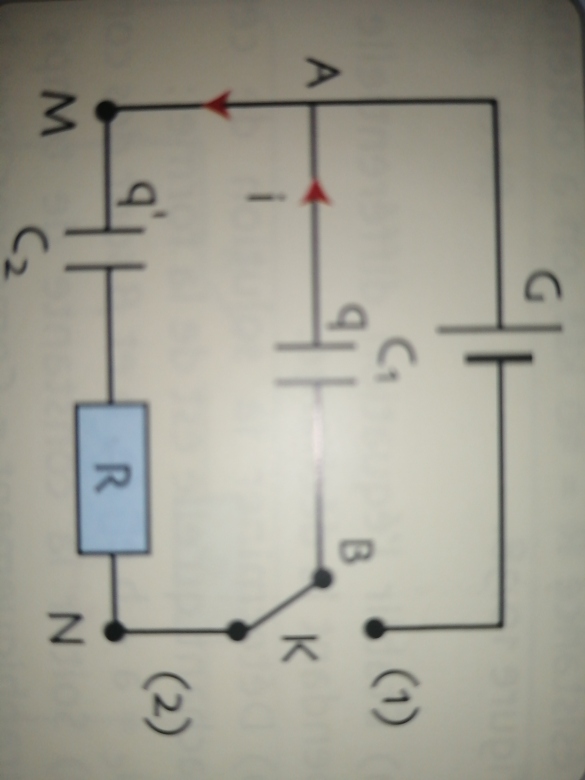
*** message déplacé ***
Bonjour,
Si vous isolez ce que j'ai entouré en rouge, que pouvez-vous écrire sur q et q' ?
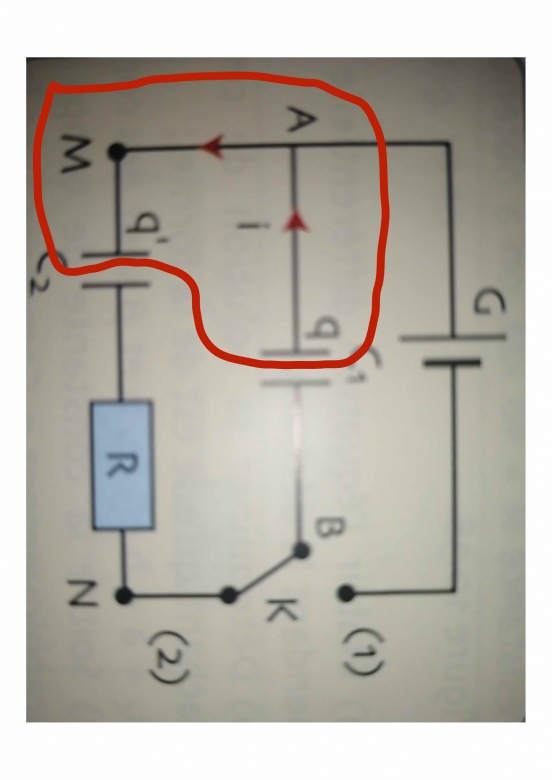
*** message déplacé ***
Quelle est la propriété de la charge électrique d'un objet isolé (ce qui est le cas de ce qui est entouré en rouge) ?
Quelle est la propriété de la charge électrique d'un objet isolé (ce qui est le cas de ce qui est entouré en rouge) ?
Je ne sais pas j'ai revue dans mon cours je n'ai pas trouvé
Pouvez vous même me dire ca veut dire quoi?
Prenons un exemple, soit une masse m et un volume V d'un gaz, je l'enferme dans un cylindre avec un piston ; je chauffe, j'appuie sur le piston ...
Qu'advient-il de m et V ?
On ne cherche pas à introduire une nouvelle grandeur, mais à savoir comment évolue m et V lorsqu'on appuie sur le piston (disons qu'avec une pompe à bicyclette on aspire, on bouche le trou et on appuie).
Désolé mais je ne comprend pas le rapport entre la relation que je veux chercher et votre exemple
Bonjour
Comment je peux demontrer cette relation ? q'=Q0-q
Sachange de Q0 c'est la charge initialle de C1
q charge de C1 et q' charge de C2
Voilà le graphe
Ya til une relation qui démontre que q'=q? Pour arriver a cette relation ou bien ya t il autre méthode ?
Merci d'avance

*** message déplacé ***
Soyons moins évasif : l'expression
"la charge est une grandeur conservative"
vous dit-elle quelque chose ?
C'est bien cela.
Donc pour le système entouré en rouge quelle est sa charge initialement et à un instant quelconque ? Appliquez ensuite la règle de conservation.
q' = constante
Non puisque q' peut s'échapper par le fil MA.
q =... = constante
Non, même raison.
Ce sont deux condensateurs différents
Oui mais relié par un fil, donc les charges peuvent aller d'un condensateur à l'autre, la charge qui se conserve est celle de l'objet isolé {électrode du haut de C2, électrode du haut de C1, fil}.
Okay donc on déduit d'après la loi regle de conservation q=q' donc q (a un instant t) =Qo-q(utilisee)
Or q=q' a cet instant
Donc q'=Qo-q
C'est ça ?
Oui c'est cela, mais il y a des problèmes de notation qui rendent votre démonstration incompréhensible (la même notation q et q' est utilisée pour des objets différents).
Je regroupe : q=q'=Qo-q !
On va garder la notation q et q' du texte (charges des condensateurs) et on va noter Q la charge totale, donc Q(t)=q+q'.
A l'instant initial q=Qo et q'=0, donc Q(t=0)=Qo
Comme Q se converse, à tout instant, q+q'=Qo




