Bonjour, pour bénéficier de l'aide, tu dois te conformer aux règles du forum.
Tu dois recopier ton problème.

------------

_{***Edit gbm => Daninho : pour compléter le propos de hdiallo, lire ceci : [***A LIRE AVANT D'AGIR***] Règles du forum***}

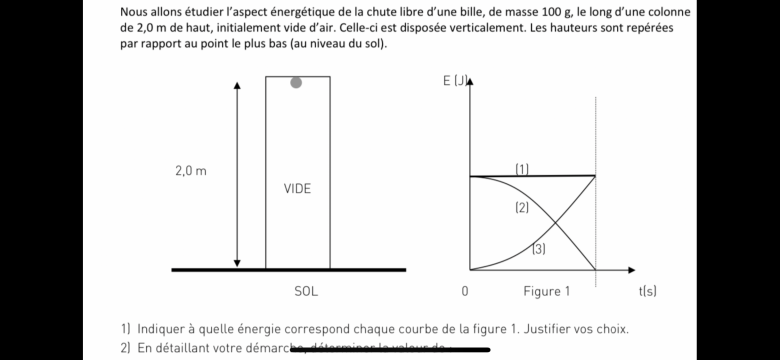
Nous allons étudier l'aspect énergétique de la chute libre d'une bille, de masse de 100g, le long d'une colonne de 2.0 cm de haut, initialement vide d'air. Celle-ci est disposée verticalement. Les hauteurs sont repérées par rapport au point le plus bas au (niveau du sol.)
2)En détaillant votre démarche, déterminer la valeur de:
a) la vitesse initiale
b) la vitesse finale
(Je vous est attaché le schéma de l'exercice avec)

Bonjour, le but de ce forum aussi est d'amener le demandeur d'aide à résoudre lui-même son exercice avec l'appui des uns et des autres.

Que proposes-tu pour la 1ère question ? Tu connais la définition des énergies cinétique, potentielle et mécanique ?

d'accord, mes réponse:
1) La courbe 1 correspond à l'énergie mécanique car l'énergie mécanique du système, est la somme de son énergie cinétique et de son énergie potentielle de pesanteur et qu'elle leur est donc supérieure.
La courbe 2 représente l'énergie potentielle de pesanteur du système sachant qu'elle varie de la même façon que l'alltitude du système.
La courbe 3 correspond à l'énergie cinétique du système, sachant qu'elle varie en sens contraire à l'énergie potentielle de pesanteur.

1)  La courbe 1 correspond à l'énergie mécanique car l'énergie mécanique du système, est la somme de son énergie cinétique et de son énergie potentielle de pesanteur et qu'elle leur est donc supérieure. Pour un solide qui tombe en chute libre dans le vide, l'énergie mécanique du système reste constante.
La courbe 2 représente l'énergie potentielle de pesanteur du système sachant qu'elle varie de la même façon que l'alltitude du système. Pour un solide qui tombe en chute libre dans le vide, l'énergie potentielle de pesanteur du système diminue.
La courbe 3 correspond à l'énergie cinétique du système, sachant qu'elle varie en sens contraire à l'énergie potentielle de pesanteur.
Pour un solide qui tombe en chute libre dans le vide, l'énergie cinétique du système augmente.

Ce que vous avez barré dans ma réponse  ce n'est pas bon ?

C'est bon mais ça ne justifie pas le choix de ces courbes.

Tu pouvais être bref et précis, en disant ceci :
- la courbe 1 traduit que l'énergie est constante dans le temps. Alors cette courbe est celle de l'Em
- la courbe 2 traduit que l'énergie diminue dans le temps. Puisque le solide tombe en chute libre dans le vide, cette courbe est celle de l'Epp.
- la courbe 3 traduit l'augmentation de l'énergie dans le temps. Puisque le solide tombe en chute libre dans le vide, cette courbe est celle de l'Ec.

d'accord merci beaucoup !, pour la question 2) je ne vois vraiment pas comment faire !

Pourtant simple sur la figure !

2.a) Tu as déjà dit que la courbe 3 traduit la variation de l'énergie cinétique dans le temps.
Que vaut donc l'énergie cinétique à l'instant initial (t = 0) ? Tu peux te servir de la courbe 3.

Connaissant Ec₀ tu peux en déduire v₀

2)a) à l'instant intial, la vitesse de la bille est nulle car sont énergie cinétique est nulle.

C'est cela !

Pour la question 2)b) la vitesse finale

Tu es en classe de 1ère, tu connais forcément un Théorème très célèbre qui lie l'énergie cinétique et le travail des forces appliquées sur un solide.

2)Dans un référentiel galiléen, la variation de l'énergie cinétique d'un solide, entre deux instants tinitial (position A) et tfinal (position B), est égale à la somme des travaux des forces extérieures appliquées au solide entre ces deux instants. Donc la vitesse finale de la bille en chute libre est: Ec(B) - Ec(A) = Wab(Fext) = 0-0 = 0

la force appliquée sur un solide de masse m qui chute librement d'une hauteur h dans le vide dans le champ de pesanteur est le poids avec comme expression: Wab(P) = P x AB x cos(a) = m x g x (za-zb) = 0,100 x 9,81 x (0-2,0) = -1,962

Soient :
- Ec0 l'énergie cinétique initiale du solide ;
- Ec l'énergie cinétique finale du solide en fin de chute.
Le Théorème de l'énergie cinétique donne :
Ec - Ec_0 = \sum{W(\vec F_{app})} = -1,962 -0 = -1,962

Pouvez vous me faire un récapitulatif

Le travail du poids d'un corps est :

Avec Oz un axe vertical ascendant.
- si le corps descend, Z_départ est supérieur à Z_arrivée et le travail du poids est positif ;
- si le corps monte, Z_départ est inférieur à Z_arrivée et le travail du poids est négatif.

Plus simplement :
- si le corps descend
-   si le corps monte.
h est la différence d'altitude entre les points de départ et d'arrivée.

donc le point d'alltitude Zb est repérée par rapport au sol donc elle fait 1,0 cm ?

Donc zb n'est pas égal à 2,0 ?

Je n'y arrive vraiment pas comparé à l'autre  exercice ce qui est bizarre car il est censé être plus facile que celui avec le chariot.

Selon tes notations :
- A est le point de départ (Z_A = h = 2,0 m)
- B est le point d'arrivée au sol, Z_B = Z_O = 0
- E_cA = 0 (car la vitesse initiale en A est nulle)
- E_cB 0, car la vitesse finale n'est pas nulle. Plus le corps descend, plus sa vitesse augmente !
- Le travail du poids de A en B est :
Tu peux te servir de cette image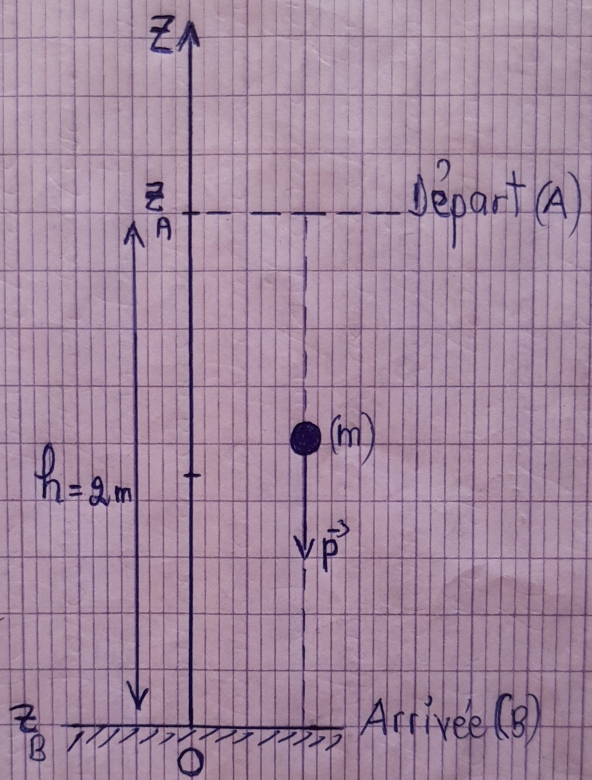
Maintenant tu peux appliquer le Théorème de l'énergie cinétique entre A et B puis tirer la vitesse finale en B, c'est-à-dire la vitesse à l'arrivée au sol.

est ce que cela est bon ? : Ec(AB) = Ec(B) - Ec(A) = Wab(Fext)
= 1/2 x m x Vb² - 1/2 x m x Va² =1/2 x 0,100 x 9,81² - 1/2 x 0,100 x 0²
Donc ce qui nous intérresse c'est la vitesse de B donc : 9,81² = 96,2 m.s^-1

Pardon, j'ai poster le mauvais calcule: : Ec(AB) = Ec(B) - Ec(A) = Wab(Fext)
= 1/2 x m x Vb2 - 1/2 x m x Va2 =1/2 x 0,100 x 9,81- 1/2 x 0,100 x 0²
ce que l'on veut c'est la vitesse finale donc :
Vfinale = Vb  = 2 x g x h = 2 x 9,81 x 0,02 = 0,626 m.s

Oui je me suis embrouiller, donc :
2)b) Ec(AB) = Ec(B) - Ec(A) = Wab(Fext)
= 1/2 x m x Vb2 - 1/2 x m x Va2 =1/2 x 0,100 x 9,81- 1/2 x 0,100 x 0²
En appliquant le Théorème de l'énergie cinétique, on aboutit à la relation de Galilée pour une chute libre sans vitesse initiale qui est :
  V² = 2xgxh V = 2xgxh =   2 x 9,81 x 2,0 = 6,26 m.s
est ce que ma formulation est bonne ?  

c'est vrai qu'il ma chatouillé Donc pour la question de la vitesse finale, je note juste : En appliquant le Théorème de l'énergie cinétique, on aboutit à la relation de Galilée pour une chute libre sans vitesse initiale qui est :
  V² = 2xgxh V = 2xgxh =   2 x 9,81 x 2,0 = 6,26 m.s

Oui, c'est ça ! Mais n'oublie pas le carré sur la vitesse, ou le radical au second membre, comme tu viens de le faire ici

je suis fatiguer, mais oui je ne l'oublierai pas

En tout cas merci encore pour votre aide !