Inscription / Connexion Nouveau Sujet
conversions et transferts de l'énergie
Bonsoir tout le monde, je suis nouveau sur ce site internet qui m'a l'air fort sympathique lorsque l'on a un problème. Je n'arrive pas a résoudre cette exercice de Physique . Et pour préciser, j'ai bien essayer de résoudre cette exercice avant de demander de l'aide, mais je n'ai pas réussi.
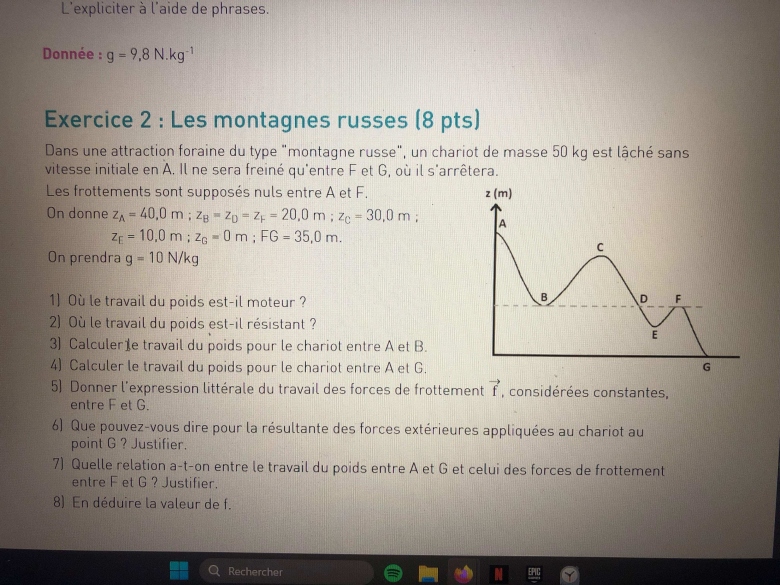
Dans une attraction foraine du type "montagne russe", un chariot de masse 50 kg est lâché sans
vitesse initiale en A. Il ne sera freiné qu'entre F et G, où il s'arrêtera.
Les frottements sont supposés nuls entre A et F.
On donne z A = 40,0 m ; z B = z D = z F = 20,0 m ; z C = 30,0 m ;
z E = 10,0 m ; z G = 0 m ; FG = 35,0 m.
On prendra g = 10 N/kg
1) Calculer le travail du poids pour le chariot entre A et B.
2) Calculer le travail du poids pour le chariot entre A et G.
3) Donner l'expression littérale du travail des forces de frottement f, considérées constantes, entre F et G.
4) Que pouvez-vous dire pour la résultante des forces extérieures appliquées au chariot au point G ? Justifier.
5) Quelle relation a-t-on entre le travail du poids entre A et G et celui des forces de frottement entre F et G ? Justifier.
6) En déduire la valeur de f.
Bonjour,
Qu'as-tu réussi à faire et où tu es bloqué ?
NB: si ton exercice a un schéma, tu peux prendre photo et joindre ici. Tu as un bouton "Img" juste en bas de ta zone de saisie, qui te permet d'attacher une image.
Bonjour, merci de me donner de votre temps pour résoudre cette exercice. J'ai mis dans mon premier message a partir la question 1), mais en réalité c'est la question 3)(image exercice) car j'ai déja réalisée les deux premières, je me suis trompé.
je vais quand même vous faire part de mes réponses à la 1) et a la 2):
1) le travail du poids est moteur en en BC car Wbc(F)(le travail d'une force) > 0 donc 0°  a
a 90 ° donc négatif. J'ai mis le W en majuscule et les lettres pour bien différencier les deux.
90 ° donc négatif. J'ai mis le W en majuscule et les lettres pour bien différencier les deux.
2) Le travail est résistant en AB car Wab(F)<0 donc 90° <a 180° donc négatif.
180° donc négatif.
Donc,Pour la question 3) j'ai appliquée la formule du travail du poids:
Wab(P) = P x AB x cos(a) = m x g x (za-zb) = 50 x 10 x (40,0-20,0) = 1,0 x 104 J
Pour la question 4), j'ai fait la même chose mais je ne sais pas si il faut aditionner entre les hauteurs ou soustraire, dans mon calcul j'ai additionner: Wag(P) = P x AG x cos(a) = m x g x cos(a) = 50 x 10 x (40,0 - 20,0) +ou-?(20,0-30,0) + (30,0 - 20,0) + (20,0-10,0) + (10,0-20,0) + (20,0-0) = 10020 = 1,0 x 104 J
j'ai donc trouver le même résultat qu'a la question 3).
Pour la question 5): L'expression littérale du travail des forces de frottement, considérées constantes entre F et G est: Wfg(F) = F x FG x cos(180) = -F x FG il demande juste de donner l'expression littérale et non calculer si je ne me trompe pas ?
Pour la question 6): Le chariot étant a l'ârret au point G, la résultante des forces extérieures au chariot est nulle, conformement au principe fondamental de la dynamique.
pour la question 7) je ne pense pas que cela soit bon : Le travail du poids entre A et G est égal a Wag(P) = P x z ou P est le poids du chariot et z la difference d'altitude entre A et G. Comme le chariot est supposé ne pas avoir de vitesse intiale à A, son énergie cinétique initiale est nulle. Selon le principe de conservation de l'énergie, le travail des forces extérieures doit être égal à la variation de l'énergie cinétique. Comme l'énergie cinétique initiale est nulle et que l'énergie cinétique finale est nulle (le chariot est à l'ârret à G ) le travail des forces extérieures doit être égal à l'opposé du travail des forces de frottement entre F et G. Donc, on a : W(P) =-W(f), soit P x z = -f x d (d étant la distance).
Pour la question 8) je ne sais donc pas si la réponse a la question 7) est correcte pour faire la 8).
Voila mes réponses a cet excercice !
Tu n'as pas répondu aux questions posées.
Allons pas à pas !
Question 1) : On demande de Calculer le travail du poids du chariot entre A et B.
Que vaut l'expression du travail du poids d'un corps de masse m, se déplaçant d'un point A (altitude ZA) à un point B (altitude ZB)?
J'ai oublier de vous donner l'image de l'exercice ! et de mettre les vraies question 1) et 2) dans mon premier message. Cela va être beaucoup plus claire avec l'image. A partir de maintenant regarder seulement les questions de l'image pour ne pas vous tromper.
Voilà ! Les questions 1) et 2) de l'image sont différentes des questions 1) et 2) que tu avais écrit dans ton message du 06-04-23 à 01:02
Maintenant, répondons aux questions de l'image.
Question 1) : où le travail du poids est-il moteur ?
Pour t'aider à répondre à la 1ère question, je te pose ceci :
Quand est-ce dit-on qu'un travail est moteur ?
Quand est-ce dit-on que le travail du poids est positif ?
Justement, les réponses des questions 1) et 2) correspondent au question 1) et 2) sur l'image. Regarder au début de mes réponses.
T'es réponses d'en haut ne sont pas vraies.
Je suis d'accord avec toi qu'un travail moteur est un travail positif (W > 0) et un travail résistant est un travail négatif (W < 0).
Mais si un corps tombe dans le champ de pesanteur g, l'altitude diminue et le travail du poids est positif. Si le corps monte, l'altitude augmente et le travail du poids est négatif. Tu peux revoir ton cours sur le travail du poids d'un corps.
Maintenant regarde bien ton image, tu verras entre quels points le corps descend et entre quels points il monte, sachant qu'il va de A vers G. Ensuite, c'est facile pour toi de répondre aux questions 1) et 2)
Donc pour la question 1)Si un corps tombe dans le champ de pesanteur g, l'alltitude diminue et donc le travail du poids est moteur et positif. Donc le travail est moteur en AB,CD,DE,FG
Pour la question 2): A l'inverse s'il le corps monte, l'alltitude augmente et donc le travail du poids est résistant donc négatif. Donc le travail du poids est résistant en BC et EF.
Maintenant on peut passer à la question 3) ?
C'est ça !
Question 3) : On demande de Calculer le travail du poids du chariot entre A et B.
Que vaut l'expression du travail du poids d'un corps de masse m, se déplaçant dans le champ de pesanteur g d'un point A (altitude ZA) à un point B (altitude ZB)?
C'est l'application directe du cours 
Wab(P) = P x AB x cos(a) = m x g x (za-zb) = 50 x 10 x (40,0-20,0) = 1,0 x 104J
Oui, le travail du poids entre A et B est
Question 4) :
Maintenant, tu appliques la même formule, mais entre A et G. C'est très facile ça, puisque tu as ZA et ZG. Le chariot va de A vers G.
Ensuite, tu fais l'application numérique.
Moi je pensais qu'il fallait additionner toutes les alltitude entre A et G et non juste A et G. Donc la réponse est : Wag(P) = P x AG x cos(a) = m x g x (za-zg) = 50 x 10 x (40,0-0) = 2,0x104J = 20kJ
Oui c'est bon :
Ou encore le travail du poids entre A et G est :
Ensuite, tu cherches les travaux intermédiaires. Tu auras le même résultat. Dans ce cas, ça sera un travail trop long.
Sais-tu que le travail du poids est indépendant du chemin suivi ? Il ne dépend que de la différence d'altitude entre le point de départ et le point d'arrivée.
Retiens ceci :
Je savais que le travail du poids était indépendant du chemin suivis mais je n'y avais pas pensera metre cela sous cette formule, merci ! maintenant ma réponse à la question 6)
Pour la question 6): Le chariot étant a l'ârret au point G, la résultante des forces extérieures au chariot est nulle, conformement au principe fondamental de la dynamique.
Oui, le système est au repos. Les forces extérieures appliquées sur lui se compensent mutuellement (système pseudo-isolé).
Donc
PS: le principe d'inertie est une conséquence du principe fondamental de la dynamique.
Récapitulons :
Question 5) :
Question 6) : (principe d'inertie)
Maintenant, la question 7) : tu connais le Théorème de l'énergie mécanique ? Système conservatif ? Système non-conservatif ?
Oui je suis d'accord avec toi que :
On est d'accord que pour la question 7), il faut juste donner l'expression et non faire le calcul ? Et aussi pouvez vous me dire quelle chose sont bonne et fausse dans ma réponse à la question 7) ?
Oui c'est correct, ce que tu as écrit. Mais il fallait juste se limiter à la relation entre le travail du poids et le travail des forces de frottement.
Tu as déjà établi que
Il suffit de remplacer le travail du poids entre A et G par son expression et le travail des forces de frottement par son expression, puis tu tire f.
Ton application numérique devrait conduire à une valeur négative de f. Pourtant tu as trouvé la bonne valeur de f. Tu as mal tiré f et ZG ne vaut pas 20,0 m.
et
Or
Donc
Je te laisse faire correctement l'application numérique.