Inscription / Connexion Nouveau Sujet
Construction d'image
Bonjour à tous,
J'ai un devoir maison de physique à faire sur les constructions d'images, sauf que pour un tracer je n'y arrive pas du coup.
J'ai OF' placé à 2.7 cm et F placé aussi à 2.7cm et OA placé aussi à 2.7 cm, mon problème est que F et A sont au même endroit, il m'est donc impossible de faire le tracé puisque je ne peux pas faire passé B par F vu que cela correspond déjà à la distance AB.
Si quelqu'un sait comment faire, pourrait-il m'éclairer?
Merci beaucoup!
En photo la figure pour que vous compreniez!
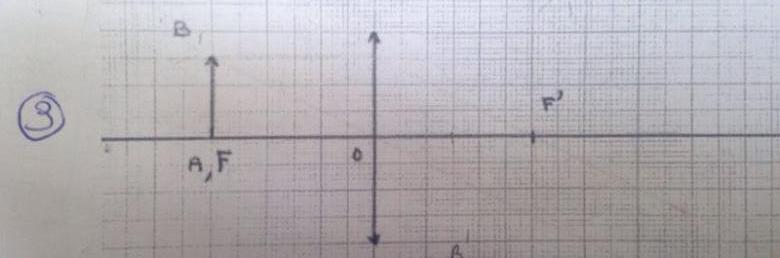
Bonjour.
Quand l'objet AB est dans le plan focal objet, l'image A'B' est rejetée à l'infini..
En traçant un rayon issu de B et passant par le centre optique O et un autre, issu de B et parallèle à l'axe optique, vous allez retrouver ce résultat.
À plus.
Merci beaucoup! Tu as raisons maintenant que j'ai tracé cela donne ça mais on me demande de vérifier à l'aide de la formule de conjugaison les résultats obtenus mais vu que c'est à l'infini je ne peux pas? Si?
mais on me demande de vérifier à l'aide de la formule de conjugaison les résultats obtenus mais vu que c'est à l'infini je ne peux pas?
Si

Veillez simplement à ne pas oublier l'algèbrisation.
Les distances se repèrent algébriquement sur l'axe optique, d'origine O, orienté positivement dans le sens de propagation des rayons lumineux, on a donc :
Donc j'ai juste à mettre ce que vous m'avez dit? Précisez que si OA' = O alors OA' est à l'infini et la relation dans votre dernier message?
Vous avez tous les éléments sous les yeux dans les deux derniers posts, il ne reste plus qu'à les assembler.

 0 !
0 !




