Inscription / Connexion Nouveau Sujet
Conservation de quantité de mouvement
Bonjour,
Les frottements sont négligeables
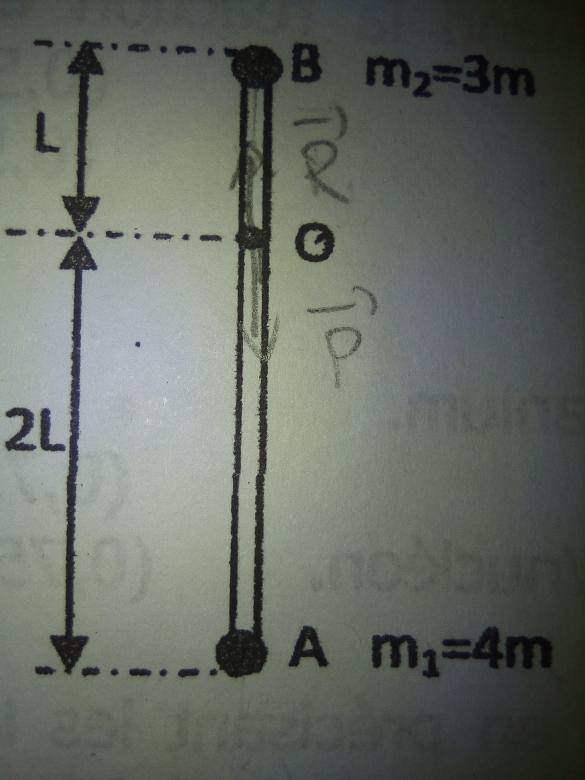
A) Deux petites billes, assimilable à des pts matériels, l'un A de masse 4m, l'autre B de masse 3m, sont placés aux extrémités d'une tige T de masse négligeable, mobile autour d'un axe horizontal passant par 0 et perpendiculaire à T.
On écarte le système dans un sens positif choisi et l'abandonne sans vitesse initiale à t=0
1) établir l'équation différentielle du mvt du système
2) Donner l'expression de l'élongation 
=f(t)
3) Quelle est la période des petites oscillations du pendule ?
4) Déterminer les vitesse deA et B au passage du système à sa position d'équilibre ?
Quelle est alors son énergie cinétique ?
AN: m=10g,L=10cm,g=10m.s-2 et =0,1 rad
B) On enlève la bille B.La tige est tjrs mobile autour de l'axe passant par 0.
On l'abandonne sans vitesse initiale
1) Quelle est la vitesse de la bille A au passage àla verticale ?
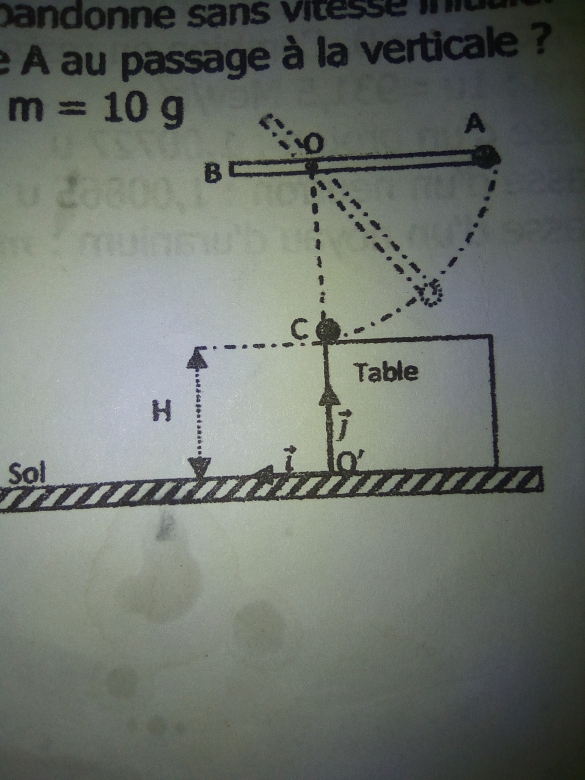
2) Lors de son passage en cette position,la bille heurte une bille C supposée ponctuelle de masse 5m, placée sur le bord d'une table.
Quelles sont les vitesse de A et C, considéré comme colinéaires, après un choc supposée parfaitement élastique ? Faire une application numérique.
A)1) pour l'eq° diff
2)
3)T=2,77s
4) à la position d'équilibre=0 rad.s-1
Donc cos(
t+
)=
1 donc la vitesse angulaire estm
2,63 rad.s-1
Est-ce correct ce que j'ai fait et quelle valeur faut-il prendre de la vitesse angulaire, le positif ou négatif ?
J'aurais besoin d'aide svp
Merci d'avance.
Bonjour
Tu n'as pas posté de schéma et je n'arrive pas à comprendre si L désigne la longueur totale de la tige ou seulement sa demie longueur. Quoi qu'il en soit, j'ai un gros doute sur la valeur littérale de la pulsation que tu obtiens. Pourrais-tu développer ton calcul ?
Sinon, au cours du mouvement, au passage de la tige à la verticale, la vitesse angulaire est positive à un passage et négative au passage suivant, une demie période plus tard. Tu as donc, comme tu l'as écrit, deux valeurs opposées possibles de la vitesse angulaire au passage à l'équilibre. Telle que la question est posée, on s'intéresse seulement aux normes des vecteurs vitesse des point A et B au passage à l'équilibre. Les deux choix vont conduire au même résultat.
Sans la figure, j'avais imaginé l'axe de rotation au milieu de la tige. Avec cette figure, l'équation différentielle et l'expression de la pulsation sont correctes. En revanche, il faut revoir la valeur de la période.
5,13 rad.s-1
/Je vois où était le problème, en fait j'ai pris 5,13 pour²
Bon, partie B maintenant
1) vitesse de A a la verticale=1m.s-1
2) c'est le choc qui me pose problème
Puisque la masse en B est enlevée et que la tige est de masse négligeable, tu es amené à étudier le choc élastique entre la masse A de vitesse horizontale (celle que tu viens de calculer) et la masse C immobile.
L'étude du choc élastique frontal de deux billes quasi ponctuelle est un grand classique que l'on trouve dans tous les cours. Il faut écrire que la quantité de mouvement et l'énergie cinétique se conserve au cours du choc.
voir ici par exemple : 
A toi d'adapter les notations ! Attention : en fonction des valeurs des deux masses, la masse A peut éventuellement repartir en arrière !
Une question,A)4) énergie cinétique du système
Ici, on calcule les énergies des points matériel en translation+énergie cinétique du système en rotation ?
Comment procéder pour trouver vitesse angulair
L'énoncé précise que la masse de la tige est négligeable. Il en est de même de son énergie cinétique. Pour la masse ponctuelle : peut importe la nature de son mouvement : l'expression de Ec est toujours la même.
Annuler
connectez vous