Inscription / Connexion Nouveau Sujet
Circuit RLC série
Bonjour Monsieur, veuillez m'assister svp
Exercice
1) Entre 2 points A et B, on monte en série une bobine d'inductance L1 et de résistance R1=25
avec une résistance pure R = 75 puis on applique entre A et B une tension sinusoïdale u(t)=220
2 sin(314t) ; u(t) est exprimé en volts.
L'intensité instantanée du courant est alors en retard de 
/3 radians par rapport à la tension instantanée entre A et B.
Trouver la valeur de L1, puis celle de Z1 L'impédance de cette portion de circuit.
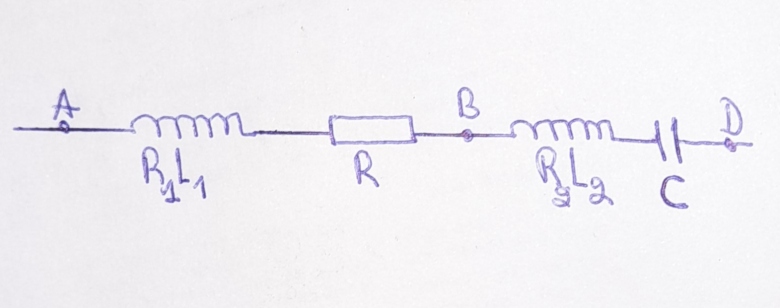
2) On met en série avec la première une autre portion de circuit BD d'impédance Z2 comprenant en série une bobine d'inductance L2=0,90H et résistance R2=100 et un condensateur de capacité C. (Voir figure).
On applique la tension précédente entre A et D.
a) En vous aidant de la construction de Fresnel, trouver la valeur de C qui vérifie la relation Z=Z1+Z2 ; Z étant L'impédance de AD.
b) Donner alors l'expression de l'intensité instantanée i(t) du courant.
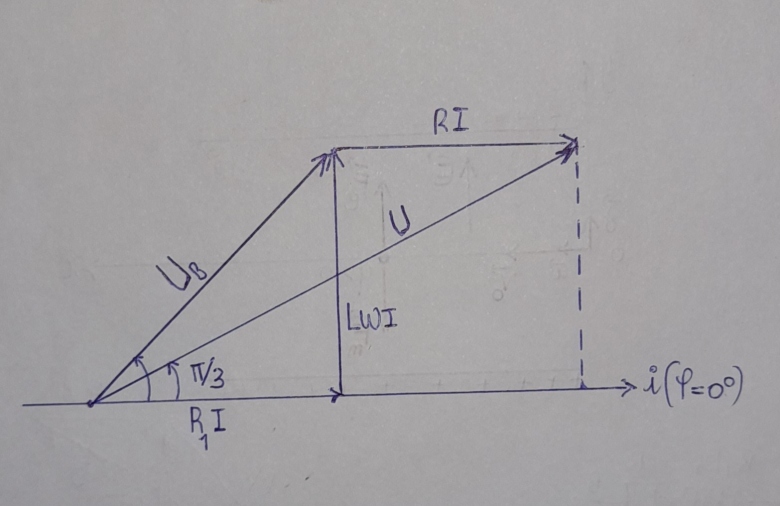
Question1: Valeur de L1 et Z1
Construction de Fresnel
tan
=(L1
/ (R+R1)
D'où L1 = (R+R1)tan /
AN : L1 = 0,55 H
Je ne sais pas si Z1 demandée est L'impédance aux bornes de la bobine ou aux bornes de AB.
Moi j'ai calculé L'impédance aux bornes de la bobine.
A mon avis, l'impédance Z1 demandée est bien celle entre A et B.Compte tenu de la précision des données et sans arrondir les calculs intermédiaires, on obtient : Z1=200
Tu as déjà tracé de la diagramme de Fresnel associé à la tension instantanée uAB.
Tu pourrais tracer maintenant le diagramme de Fresnel associé à la tension instantanée uBD.
Ensuite, sachant que pour un circuit série les tensions instantanées s'ajoutent : uAD=uAB +uBD, ... Je te laisse continuer...
Salut, j'étais en déplacement pour un village...Guinée profonde...pas de connexion
Merci Vanoise
Maintenant voici le diagramme de Fresnel pour la portion BD.
C'est bon mon diagramme ?
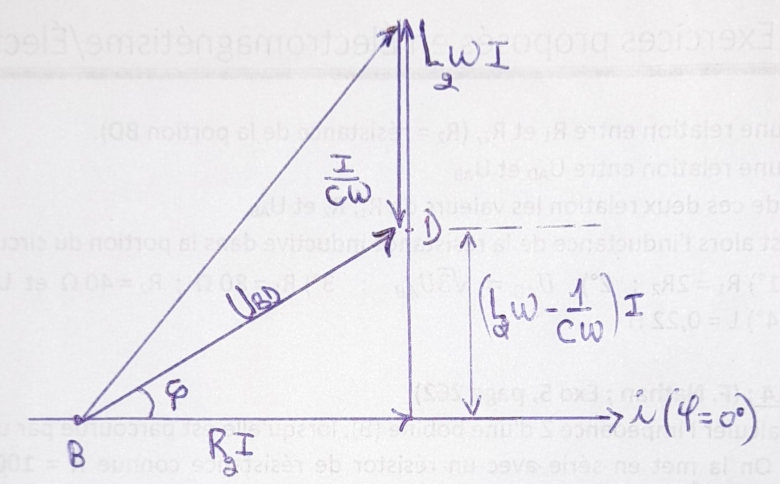
Pour moi, en appliquant la tension u(t)=2202 sin(314t) Entre A et D, les impédances Z de AD et Z1 de AB devaient être égales (Z=Z1) puisque :
UAB=UAD=Z1I=ZI
Or Z=Z1+Z2 
Z2=0
Donc (R2)²+(L2-1/C)²=0
Je tire C dans cette relation et je trouve :
C = 8,3 
F
D'accord avec le diagramme de Fresnel concernant UBD. La suite est plus délicate et ne manque pas de subtilité...
Puisqu'il faut vérifier : Z=Z1+Z2, la multiplication de chaque terme par l'intensité efficace commune à tous les dipôles puisqu'il s'agit d'une association série, conduit à la relation suivante entre les trois valeurs efficaces :
(relation 1)
Or, la loi d'addition sur les tensions instantanées conduit à :
(relation 2)
ce qui conduit à la relation que tu connais entre les vecteurs de Fresnel associés :
(relation 3)
En tenant compte des relations 1 et 3, tu es amené à te poser la question suivante, sûrement traitée en cours de math :
“À quelle condition, la norme de la somme de deux vecteurs non nuls est-elle égale à la somme des normes de ces deux vecteurs ?”
La norme de la somme de deux vecteurs non nuls est égale à la somme des normes de ces deux vecteurs, cela veut dire que les deux vecteurs sont parallèles et de même sens, si j'ai bien compris
U²AD=U²AB+U²BD+2.UAB.UBD.cos
Or si les deux vecteurs sont parallèles, =0
Nous pouvons écrire :
U²AD=U²AB+U²BD+2.UAB.UBD
Maintenant, je ne comprend pas comment jouer entre ces relations et calculer la capacité C demandée
cela veut dire que les deux vecteurs sont parallèles et de même sens, si j'ai bien compris
Oui et la démonstration faite au message suivant est correcte.
A mon avis, le plus simple pour obtenir la valeur de C demandée consiste à remarquer que, les deux vecteurs de Fresnel ayant même direction :
tan(
1)=tan(2),
1 étant l'avance de phase de uAB(t) par rapport à i(t) et 2 étant l'avance de phase de uBD(t) par rapport à i(t)Je crois que tu as commis une erreur de signe dans l'expression littérale de C. Elle conduit à une valeur numérique de C négative !
Je crois que tu as commis une erreur de signe dans l'expression littérale de C. Elle conduit à une valeur numérique de C négative !
Ah d'accord, je vois
Mais je trouve toujours une valeur de C positive
C
29,11 FMerci.
b) Expression de i(t)
Je pose i(t)=I2.sin(t+) ; avec =314 rad/s
Z=Z1+Z2
et
Ou encore cos2=R2/Z2
Z2=R2/cos2=100/cos(/3)=200
Donc Z=Z1+Z2=400
Pour déterminer l'intensité efficace, j'utilise la loi d'Ohm aux bornes de AD : UAD=ZI
Soit I=UAD/Z
AN : I = 220/400 = 0,55 A
Maintenant pour trouver le déphasage entre uAD(t) et i(t), je pose :
Cos=
R/Z
Cos=(R1+R+R2)/Z
Je trouve cos=200/400=½
Donc =/3 rad
Alors : i(t)=0,552.sin(314t + /3)
Si je comprend bien, je dois déterminer la nature du circuit (capacitif ou inductif). Pour cela je compare (L1+L2) à 1/(C)
Je constate que (L1+L2) est supérieur à 1/(C); donc le circuit est inductif c'est-à-dire que u(t) est en avance sur i(t).
Donc i(t) = 0,552.sin(314t-/3)
Et u(t)=2202.sin(314t)
Est-ce vrai ?
Bravo ! Tout ce que tu as écrit est correct. Tu aurais quand même pu te simplifier la vie en tenant compte de tes considérations précédentes sur les vecteurs de Fresnel associés au trois tensions instantanées. Puisque ces vecteurs ont même direction :
= 1 = 2 .
Ton premier résultat est correct. Puisque u(t) est en avance de /3 par rapport à i(t), i(t) est en retard de phase de /3 par rapport à u(t).
Annuler
connectez vous