Inscription / Connexion Nouveau Sujet
Circuit RLC avancé, courant sinusoïdale
Bonjour,
J'ai un exercice dont je ne comprends pas un des résultats.
Je suis dans un contexte d'un circuit électrique a courant sinusoïdale, le but final étant de trouver V0.
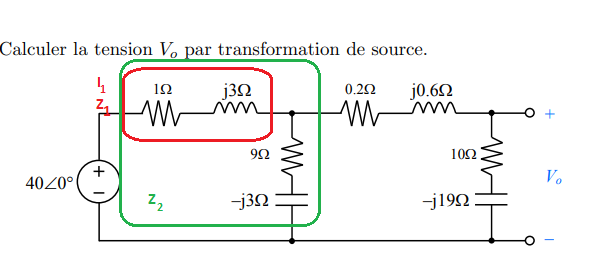
Pour faire ça on va simplifier chaque partie du circuit, on a donc :
Z1 = 1+j3
et Zequivalent de Z2 on a :
Z2 = ( (1+j3) * (9-j3) ) / ( (1+j3)+(9-j3) )
De mon coté en simplifiant je trouve :
Z2 = (9 + 24j - 9j²) / 10
Mais le résultat simplifié du cours est :
Z2 = (18+ 24j) /10 = 1.8+2.4j
Et je suis incapable de trouver comment simplifier pour arriver a ce résultat.
Pouvez vous m'aidez s'il vous plait?Y aurait il une notion que j'ai oublié?
Merci d'avance.
Bonjour Pirho,
Dans le calcul j est un nombre complexe, et en me levant ce matin je viens de réaliser que du coup j²=-1.
...jai énornément de mal a accepter que cela soit physiquement réaliste, il va falloir absolument que je vérifie en reproduisant et en vérifiant dans la réalité.
En tout cas, merci beaucoup d'avoir essayé de me guider 
Bonne journée
Oui, une fois cette étape résolue, tous le reste a suivi 
Mais mes peines ne sont pas finies, a peine l'exercice suivant commencé que je recommence a avoir du mal avec une simple simplification d'équation.
J'ai :
0 = -10.6+(V1)/10 + (V1-V2)/(1+j2) et
0 = (V2 - V1) / (1+j2) + V2/-j5 + (V2-20Ix)/20
Avec Ix = (V1-V2)/(1+j2)
Et je sais qu'au final V1 = 68.40 - j16.80 et V2 = 68.00-j26
Ca fait maintenant plus d'une heure que j'essaye de refaire toutes les étapes en partant des equation du début pour arriver aux resultats de V1 et V2, mais j'ai confiance, je vais finire pas y arriver 
Bon, je n'y arrive pas , j'aurais besoin d'un petit coup de main s'il vous plait.
je re-décris la situation initiale, ou cas un point m'aurais échappé.
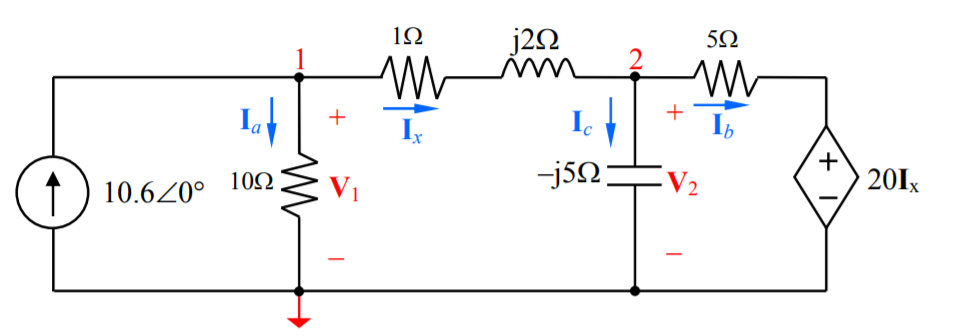
On a le circuit suivant (ref : image).
On fait la somme des courants aux noeuds (1 et 2).
Au noeud 1 on a :
0 = -10.6+V1/10 + (V1-V2)/(1+j2)
Au noeud 2 on a :
0 = (V2 - V1) / (1+j2) + V2/-j5 + (V2-20Ix)/20
(Je ne sais pas pourquoi c'est -20Ix / 20, je comptais chercher plus tard pourquoi).
Et on a la relation Ix = (V1-V2)/(1+j2)
Avec comme résultat donné :
V1 = 68.40 - j16.80 et V2 = 68.00-j26
Mon but était de partir des équations du début pour arriver aux résultats de V1 et V2
Pour faire ca je voulais me débarrasser dans mon equation, au choix, de tous les V1 pour leurs V2 équivalent, histoire de pouvoir résoudre V1 = a +bj
J'ai donc commencé par simplifier, avec :
0 = 10.6+V1/10 + (V1-V2)/(1+j2) soit 10.6+V1+Ix
où en developpant, -V2 = 10.6+21.2j+9V1/10+V1j/5
Pour essayer de me debarrasser de ma relation V1j ,j'ai notament essayé de de repartir des équations du débuts :
-10.6+V1/10 + Ix = -Ix +V2/-j5+V2/20 -Ix = 0
Que j'ai développé avec Ix = 10.6-V1/10 pour avoir la forme simplifié :
106-2V1 = -V2j + V2/4
Puis j'ai remplacer les V2 par l'équation précedente -V2 = 10.6+21.2j+9V1/10+V1j/5
Mais j'ai pas réucis a me debarraser du V1j
(l'equation simplifié que j'ai trouvé est : (78V1-7V1J)/40 = -87.225-15.9j )
Mais je pense etre partit dans toutes les directions, est ce que vous auriez un conseil/une méthode a me donner pour me debloquer, svp? 
1) poste ton schéma; ça permettra de vérifier tes équations de départ
2)si tu as encore le temps, repasse sur le site en début de soirée car je ne suis plus disponible maintenant, sorry!
Oups voici le schema, j'ai du oublier.
Pas de soucis, encore merci beaucoup de passer du temps pour m'aider 
remarque : ton écriture des grandeurs complexes est peu habituelle; je l'ai respectée!
au noeud 1 essaye d'écrire
sauf erreur de ma part,au noeud 2 on a
au lieu de
0 = (V2 - V1) / (1+j2) + V2/-j5 + (V2-20Ix)/20
oups! au lieu de
au noeud 1 essaye d'écrire V1=....
après transformation écrit
Merci énormément Pirho, avec Ib correct, je pense que je vais réussir a me débloquer  il y a du y avoir une erreur dans l'énoncé.
il y a du y avoir une erreur dans l'énoncé.
quand tu dit :
ton écriture des grandeurs complexes est peu habituelle
Qu'est ce que tu entends par la? ce n'est pas un choix conscient, j'ai trouvé cette définition :
http://ressources.unisciel.fr/ramses/511-14-nbr-complexes/co/fa301_2_1.html
(Je ne pouvais pas copier le texte, certaines parties sont des images).
Est ce que tu peux me donner un exemple d'un cas que j'ai mal fait, pour que je puisse me mettre a la norme?

Encore merci d'avoir passé du temps pour m'aider.
en principe, dans le cas de grandeurs complexes on écrirait
ou
ou
ou
...
mais certains auteurs, par facilité typographique, laisse tomber les "barres"