Inscription / Connexion Nouveau Sujet
Circuit RL bobine et conducteur ohmique en parallèle
Bonjour tout le monde !
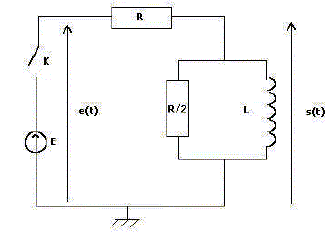
Svp j'arrive pas à trouver l'equation differentielle pour ce curcuit, sachant qu'on doit la trouver par la loi des nœuds.
Et merci
Bonsoir
Tu peux partir de la loi des nœuds : i=i1+i2 et exprimer chaque intensité en fonction de e(t), s(t) et des dérivée éventuelles de ces tensions par rapport au temps.
Deux astuces pour t'aider :
1° : l'intensité du courant principal peut s'écrire :
2° : l'équation différentielle ainsi obtenue fait intervenir une primitive de s(t). Il suffit alors de dériver par rapport à t tous les termes de l'équation pour la faire disparaître.
Bonsoir
Tu peux partir de la loi des nœuds : i=i1+i2 et exprimer chaque intensité en fonction de e(t), s(t) et des dérivée éventuelles de ces tensions par rapport au temps.
Deux astuces pour t'aider :
1° : l'intensité du courant principal peut s'écrire :
2° : l'équation différentielle ainsi obtenue fait intervenir une primitive de s(t). Il suffit alors de dériver par rapport à t tous les termes de l'équation pour la faire disparaître.
Merci énormément !
Bonsoir
Tu peux partir de la loi des nœuds : i=i1+i2 et exprimer chaque intensité en fonction de e(t), s(t) et des dérivée éventuelles de ces tensions par rapport au temps.
Deux astuces pour t'aider :
1° : l'intensité du courant principal peut s'écrire :
2° : l'équation différentielle ainsi obtenue fait intervenir une primitive de s(t). Il suffit alors de dériver par rapport à t tous les termes de l'équation pour la faire disparaître.
Pardon, mais je suis bloqué sur l'intègrale de s(t). Tu peux stp m'aider à la trouver ?
En notant i2 l'intensité du courant, supposé correctement orienté, à travers l'inductance :
Ensuite : la dérivée par rapport à t d'une primitive de s(t) est s(t).
Sinon, on peut aussi arriver au résultat en utilisant l'expression dérivée de la loi des nœuds :
Il suffit d'exprimer ces trois dérivées en fonction de R, L et des dérivées première et seconde de s(t) et de e(t).


