Inscription / Connexion Nouveau Sujet
Circuit intégrateur et derivateur
Bonjour j'ai besoin de votre aide svp
Exercice :
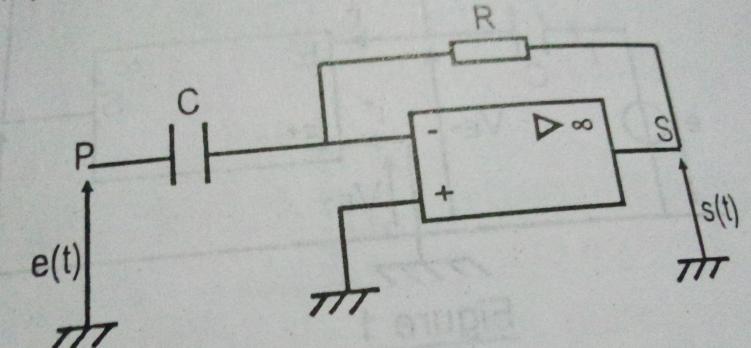
Dans le montage de la figure ci-contre , l'amplificateur opérationnel (AO) est parfait et il fonctionne en régime linéaire. Ses tension de saturation ±Vsat sont égales à ±13V.
On donne : C=50 F et R=20 K
F et R=20 K .
.
1. Établis de façon littérale , la tension de sortie s(t) en fonction de R , C et de la dérivée par rapport au temps de e(t).
Indique le type de montage dont il s'agit.
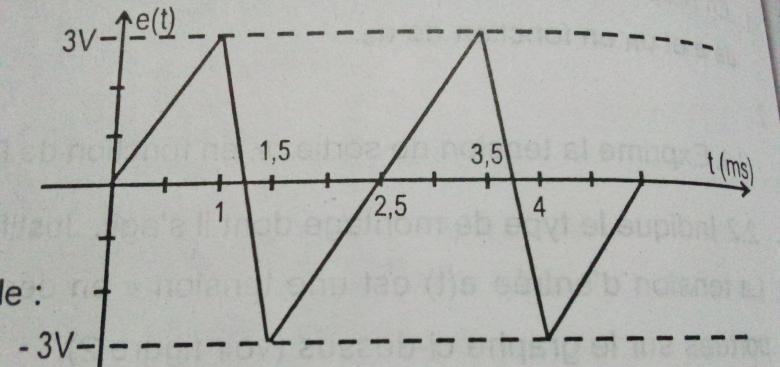
2. La tension d'entrée e(t) est la tension en dent de scie représentée ci-dessous.
En déduis:
_ La période T et la fréquence N de ce signal ,
_ La forme du signal de sortie s(t)
Réponses :
1.
D'après la loi des mailles :
-e(t)+uc(=0
<=> uc=e(t). (1)
D'après la loi des mailles :
-s(t)-uR=0
<=> uR=-s(t). (2)
On a : uR=Ri
Or i=dq/dt
<=> i=d(C.uc)/dt
<=> i=C.duc/dt
uR=RC.duc/dt or uc=e(t)
uR=RC.d[e(t)]/dt
(2): s(t)=-uR
s(t)=-RC.d[e(t)]/dt
Il s'agit d'un circuit derivateur .
2. T se lit sur la représentation graphique de e(t) en fonction de t
T=2,5.10-3 S
N=1/T=1/(5.10-3)=500Hz
N=500Hz
Globalement d'accord avec ce que tu as fait. 
Juste deux précisions :
* plus que la loi des mailles, c'est plutôt le fait que VE-=0 en régime linéaire qui permet d'obtenir les relations que tu as écrites (relations tout à fait correctes).
* Il s'agit bien d'un montage dérivateur. On précise en général : "dérivateur inverseur" à cause de la présence du signe "-" qui apparaît dans l'expression de s(t).
D'accord avec tes valeurs de la période et de la fréquence. Il te reste à déterminer les valeurs de : deux valeurs différentes selon les valeurs de t...
J'ai manqué d'attention dans mes vérifications. Si T =2,5ms comme tu l'as écrit, la fréquence ne vaut pas 500Hz.
N=400 Hz
Je vois , je dois trouver la valeur de de/dt pour :
_ t [0 ms ;1 ms]
[0 ms ;1 ms]
_ t [1ms ; 1,5 ms]
[1ms ; 1,5 ms]
_ t [1,5 ms ; 3,5 ms]
[1,5 ms ; 3,5 ms]
_ t [3,5 ms ; 4]
[3,5 ms ; 4]
_ t [4 ms ; 5ms]
[4 ms ; 5ms]
C'est bien cela mais en fait : cela te fait seulement deux coefficients directeurs différents à déterminer.
Pour t ] 0 ms ; 1ms ] ∆e/dt=3000
] 0 ms ; 1ms ] ∆e/dt=3000
e=(∆e/dt)t
e=3000t
Us=-RC.de/dt=3000
Us=-20.103×50.10-9×3000
Us=3V
Pour [1 ms ; 1,5]
Us=-20.103×50.10-9×(-12000)
Us=12 V
Je suppose comme toi : C=50nF et pas 50µF. nano se note tout simplement "n" et pas " "
"
La courbe e=f(t) étant constituée de segment de droites, il est possible d'écrire que la dérivée est égale au coefficient directeur de chaque segment :
Les valeurs numériques étant mesurées en V/s.
Sinon, tes applications numériques me semblent correctes. As-tu représenté la courbe s=g(t) ?
Oui je pense : tu traces dans le même repère les allures des deux courbes e(t) et s(t) puis tu réponds à cette question en guise de conclusion.