Inscription / Connexion Nouveau Sujet
Circuit électrique
Bonjour,
Pouvez-vous me dire si mes réponses sont correctes s'il vous plait ?
1) Trouver la résistance équivalente de tout le circuit.
2) En déduire l'expression de i.
3) Donner les expressions de i0 ; i1 ; i2 ; i3 et U0 ; U1 ; U2 ; U3.
1) J'ai trouvé Réq = 22R/5
2) i = 5E/22R
3) i0 = U0 / 2R ; i1 = U1/2R ; i2 = U2/2R ; i3 = U3/2R
U0 = i0*2R ; U1 = i1*2R ; U2 = i2*2R ; U3 = i3*2R
On peut aussi dire que U0 = U1 = U2 = U3.

PDF - 19 Ko
Bonjour
1) J'ai trouvé Réq = 22R/5
Tu peux expliquer comment tu es arrivée à ce résultat ?
La méthode la plus simple consiste à simplifier pas à pas le circuit à partir de la droite sur le schéma.
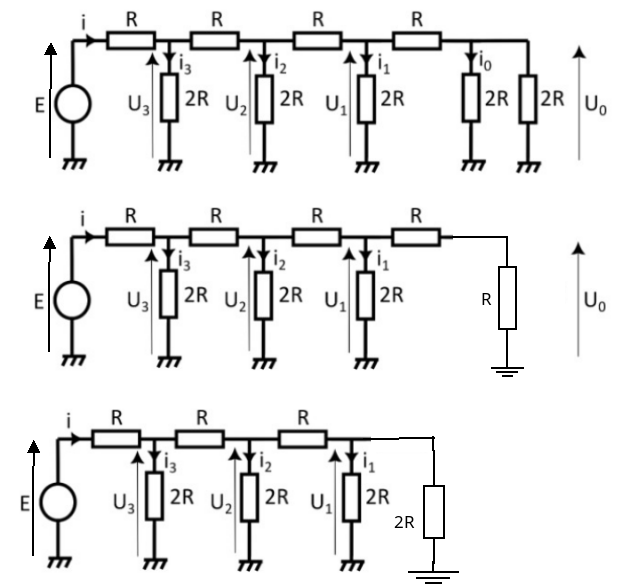
Il y a 5 résistances en parallèle et 4 résistances en série.
On a 4R pour la résistance équivalente des résistances en série et 2R/5 pour la résistance équivalente pour les résistances en parallèle.
On additionne 4R + 2R/5 = 22R/5.
Les résistances verticales sur le schéma ne sont pas en parallèle (sauf les deux dernières). Leurs bornes inférieures sont toutes reliées à la borne négative du générateur mais leurs bornes supérieures ne sont pas communes car séparées par des résistances horizontales.
Les résistances horizontales sur le schéma ne sont pas en série : elles ne sont pas parcourues par le même courant.
Je t'ai indiqué une méthode dans mon précédent message. Considère les deux résistances "verticales" de droite. Elles sont en parallèle et peuvent être remplacées par une résistance unique égale à la moitié de 2R donc égale à R.
Cette résistance équivalente R est en série avec la résistance R horizontale de droite. Cela constitue un diviseur de tension conduisant à :
(remarque utile pour la question 2). Cette association possède une résistance équivalente égale à 2R et est en parallèle avec la résistance 2R parcourue par i1... On peut donc refaire le raisonnement précédent... Il conduira à :
Refaire à nouveau ce raisonnement va conduire à :
et
mais aussi à une expression extrêmement simple de la résistance équivalente.
Reprend pas à pas ce raisonnement en t'aidant de schémas pour mieux comprendre.
Cela veut dire que chaque résistance verticale 2R est en série avec une résistance horizontale R (sauf à droite où on a une résistance équivalente verticale R)?
On a donc comme résistance totale équivalente en partant de droite : Réq = R + R + 2R + R + 2R + R + 2R + R = 11R ?
Non ! N'essaie pas de deviner une réponse mais raisonne pas à pas. Ce n'est pas la première fois que cette remarque t'est faite.
As-tu compris le passage du premier schéma au troisième ?
Si oui : tu vois bien que, sur le troisième schéma, les deux résistances 2R verticales de droite sont équivalentes à une résistance R. Cela revient à reproduire sur le schéma 3 le raisonnement fait précédemment sur le schéma 1 et ainsi de suite...
Oui, on arrive à gauche avec une résistance égale à 2R.
A chaque fois, la résistance équivalente des 2 résistances 2R en parallèles est R. Et après, on fait à chaque fois R+R puisqu'il s'agit de 2 résistances en série.
Du coup, est-ce que la résistance équivalente totale du circuit serait de 2R ?
Oui ! Je te laisse continuer en tenant compte de mes remarques précédentes sur les différentes tensions.
Du coup, on a : i = E / 2R
On sait que U0 = U1/2 ; U1 = U2/2 ; U2 = U3/2 et U3 = E/2
On a donc i0 = U0 / R = U1 / 2R
i1 = U1 / R = U2 / 2R
i2 = U2 / R = U3 / 2R
i3 = U3 / R = E / 2R
on a : i = E / 2R
On sait que U0 = U1/2 ; U1 = U2/2 ; U2 = U3/2 et U3 = E/2
Oui ; ce qui conduit, en utilisant la loi d'Ohm, à :
Je te laisse terminer...
Maintenant, on met des interrupteurs et on mesure le courant it. Il faut donner l'expression de it en fonction de E et de R.
Ici, j'utilise la formule it = E / Réq, mais je ne vois pas par où commencer pour trouver Réq.
Pouvez-vous m'aider s'il vous plait ?

PDF - 21 Ko
Sauf indication contraire, tu peux considérer l'ampèremètre comme un dipôle de résistance négligeable. Dans ce cas, basculer d'une position à l'autre un ou plusieurs interrupteur(s) ne modifie pas les intensités déjà calculées puisque l'autre borne de l'ampèremètre est aussi reliée à la borne négative du générateur. Dans le cas particulier de ton schéma :
It= I3 + I0
les valeurs de I3 et I0 étant celles déjà calculées. Ce montage a pour but de vérifier expérimentalement la théorie faite dans les questions précédentes.
Oui dans le cas particulier du schéma. On peut envisager de nombreuses autres valeurs selon les positions des interrupteurs.
Comment puis-je expliquer le fait que ce circuit puisse être utilisé comme un convertisseur CNA ?
Je peux dire qu'un interrupteur qui est fermé représente un bit de valeur 1 et qu'un interrupteur qui est ouvert représente un bit de valeur 0 ?
Soit le nombre "abcd" en base 2 où a,b,c et d sont des entiers égaux à 0 ou 1. La valeur de ce nombre est :
a est associé à l'interrupteur de gauche, b au suivant vers la droite et ainsi de suite. Si un interrupteur assure la liaison à l'ampèremètre, on lui associe la valeur “1”, sinon, on lui associe la valeur “0”.
Les rapports d'intensités ont déjà été étudiés. Je te laisse compléter et conclure.
a = d = 1 et b = c = 0
Donc N = 9
Cela veut dire que I(t) = I3 + I0 = 9E/32R
On retrouve le même résultat que celui trouvé précédemment.
Oui bien sûr mais l'objet de mon précédent message était de t'aider à répondre à la question avec "abcd" quelconque :
Comment puis-je expliquer le fait que ce circuit puisse être utilisé comme un convertisseur CNA ?
Le circuit peut être utilisé comme un convertisseur car il traduit des combinaisons de valeurs binaires en un niveau de courant mesurable par l'ampèremètre.
Le signal analogique est proportionnel à la valeur numérique binaire.
Donc le circuit utilise les interrupteurs pour créer un courant proportionnel à une valeur binaire, ce qui permet de convertir le signal numérique en un signal analogique qui est mesurable ?