Inscription / Connexion Nouveau Sujet
Cinetique chimique
Bonjour je rencontre quelque difficulté pour résoudre un exercice. Merci d avance pour votre aide.
voici l'exercice.
On étudie la cinétique de synthèse de l'iodure d'hydrogène H2 + I2 → 2HI
Pour cela, on porte à 450°C quatre ballons numérotés 1; 2; 3 et 4 qui contiennent chacun un mélange réactionnel identique: 0,5.10 mol de I2 et 5,0.10 mol de H2.
Ces ballons sont maintenus à cette température pendant des durées t différentes puis brutalement refroidis
Le diode restant est dosé avec une solution de thiosulfate de sodium de concentration molaire
C 0,05 mol/L. On met quelques gouttes d'empois d'amidon.
1-) Quel est le rôle de l'empois d'amidon?
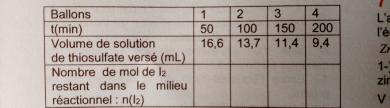
2- On a obtenu le tableau de résultats suivants (dosage du diiode en excès).
Ecrire l'équation-bilan de la réaction de dosage
étudié.
Compléter le tableau ci-dessus.
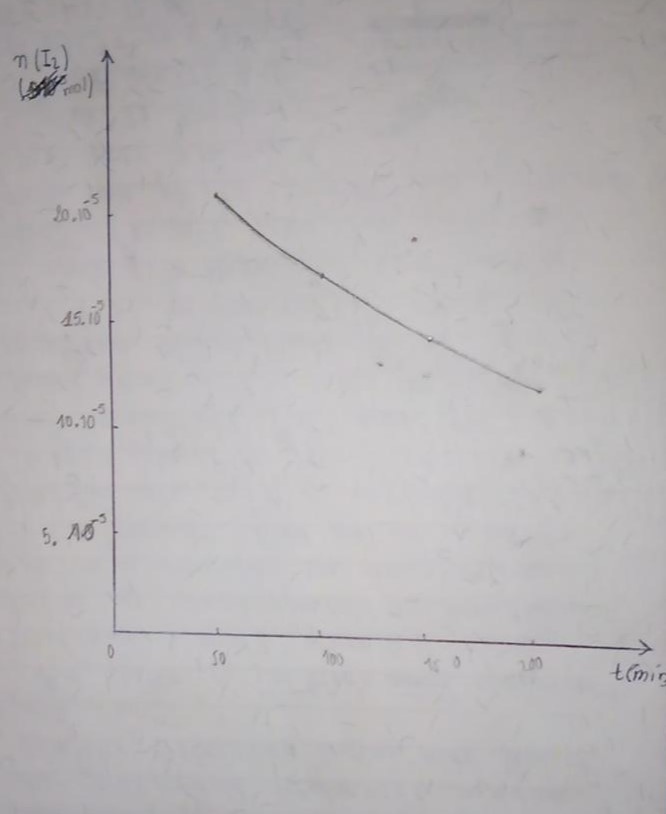
3-) Tracer le graphe n(12) = f(t)
Echelle: 1cm pour 25 min; 1 cm pour 5,0.10% mol. Trouver la vitesse instantanée de disparition du diiode à la date t=0 puis à la date t = 100 min. Si la vitesse de disparition du diiode était constante et égale à sa valeur à la date t =0, quelle serait le nombre de mol de diiode dans le milieu réactionnel à la date t = 200 min ?
Voici ce que j'ai fait pour l'instant.
1) sachant que le diiode bleuit avec l'amidon, la disparition de la couleur bleu sera un indicateur de fin de réaction
2) équation bilan
I2 + 2 S2O32-  2I- + S4 O62-
2I- + S4 O62-
Pour compléter le tableau j'ai eu la relation
n(I2)=CV/2 a partir du bBM
Bonjour
Qu'as-tu réussi à faire pour l'instant ? Qu'est ce qui te bloque ?
Ce qu me bloque c'est qu a partir du tableau et même du graphe (sans utiliser le logiciel on peut pas vraiment déterminer la vitesse a t=0
Ok pour ce que tu as fait mais il faut revoir la courbe :
Préciser les axes et les échelles ;
Surtout : ne pas tracer la droite moyenne mais une courbe à main levée avec pour asymptote horizontale n(I2)=0. Tu seras ensuite amené à tracer diverses tangentes à cette courbe.
Et enfin mon dernier soucis se trouve au niveau de la dernière question, je crois qu'on devrait passer par la loi exponentiel mais pour déterminer la constant k, j'ai des contradictions
Ok pour ce que tu as fait mais il faut revoir la courbe :
Préciser les axes et les échelles ;
Surtout : ne pas tracer la droite moyenne mais une courbe à main levée avec pour asymptote horizontale n(I2)=0. Tu seras ensuite amené à tracer diverses tangentes à cette courbe.
D'accord
Problème : je n'arrive pas à déchiffrer les puissances de 10 que tu as écrites. A ce qu'il me semble, la quantité de I2 restante à la date t=50min vaut 41,5.10-5mol, ce qui pourrait correspondre à ta première courbe fournie (en explicitant l'échelle) mais pas à la seconde.
Pour la vitesse initiale : il faut aussi placer le point sur la courbe correspondant à t=0 puis tracer la tangente en t=0 à la courbe. Le coefficient directeur de cette tangente te donnera, au signe près, la vitesse de disparition initiale. Procéder de même pour t=100min.
Impossible pour moi de lire la quantité initiale de I2 : la puissance de 10 n'apparait pas.
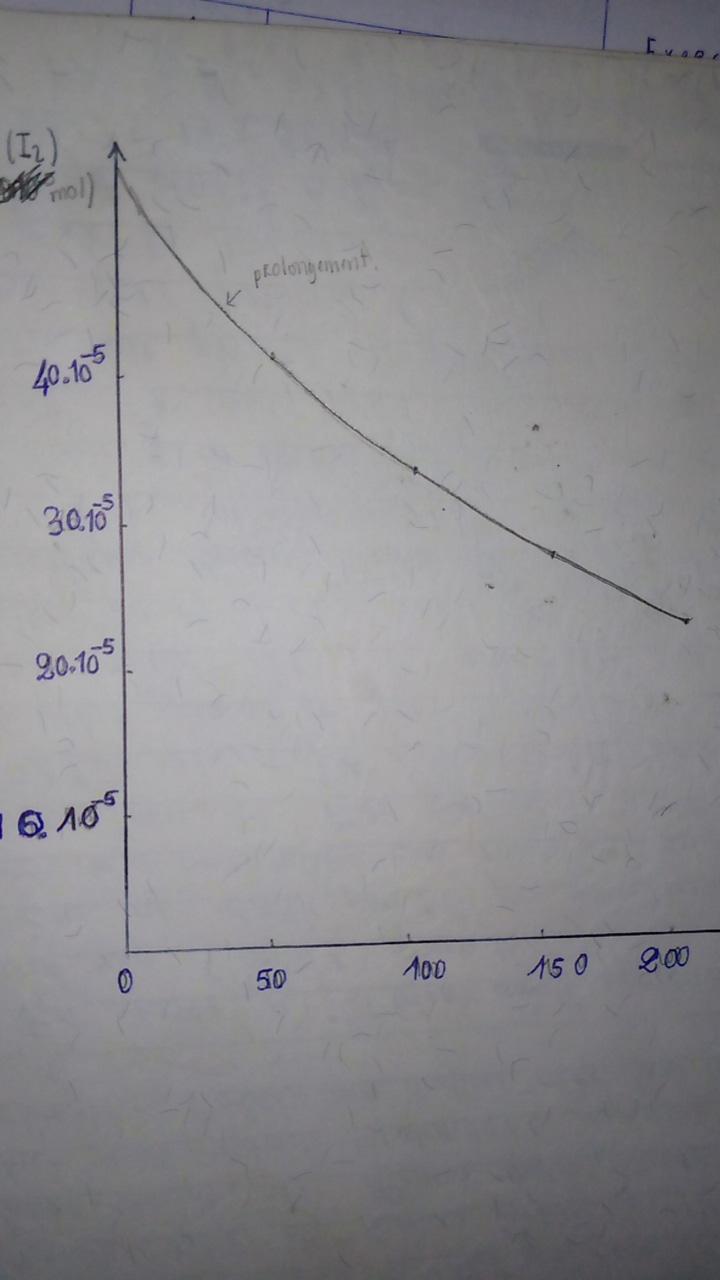
pour placer le point a t=0 il faut faire un prolongement, si oui est ce que ce serait précis de procéder ainsi.
Desole je vous envoie une image plus claire
A ce je crois avoir deviné, la quantité initiale de I2 vaut 50.10-5mol. Cela donne la courbe que tu obtiens. Voici ce que j'obtiens de mon côté en traçant aussi la tangente en t=0.
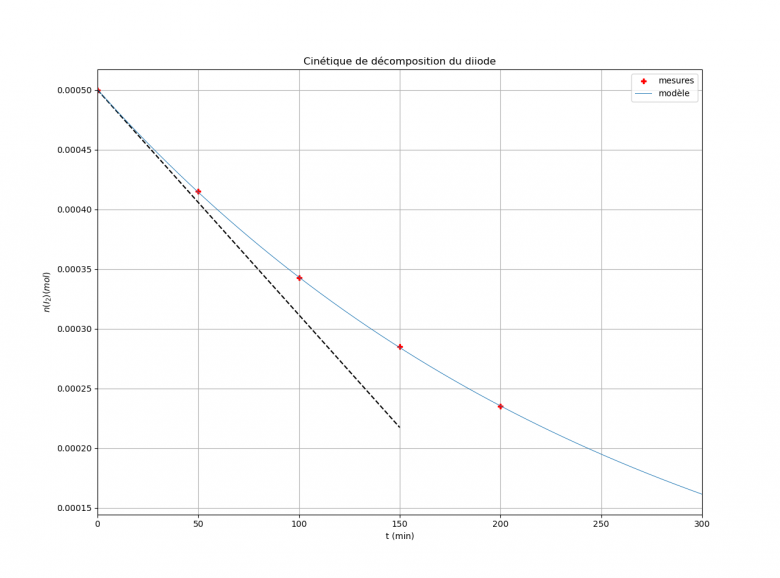
Je vois, je pensais je n'avais pas le droit de prolonger.
De mon coté je trouve 5,35.10-5
pour la vitesse de formation du diiode j'ai trouvé 3,3.10-2 a t=0 et 9,3.10-3 pour t=100 min
pour la dernière question j ai pense a a loi exponentielle mais déjà le fait n a t égale a 0 soit constant entraine quoi au niveau de notre graphe. Il est tjrs utilisable pour calculer des valeurs afin de sortir la constante ?
je pensais je n'avais pas le droit de prolonger.
De mon coté je trouve 5,35.10-5
Je me suis contenté de lire l'énoncé, pas de prolonger la courbe, en espérant bien avoir "deviné" la puissance de 10 !
Pour les vitesses, ton ordre de grandeur n'est pas bon. Réfléchi : pendant les 100 premières minutes la quantité de diiode ne diminue que d'environ 16.10-5mol, ce qui donne une vitesse moyenne de disparition sur les cent premières minutes de seulement 16.10-7mol/min environ. Bien sur, la vitesse instantanée n'est pas égale à la vitesse moyenne mais l'ordre de grandeur est le même !
Oui c'était bien 5.10-5
A t=0 on a n0=5.10-5mol a t=100 min j'ai n=3.425.10-4mol
Du coup pourquoi vous dites que la quantité varie de 1,6.10-5mol
Ma question parait surement bête mais je vois vraiment pas
Le tableau de mesures est cohérent avec une quantité initiale de diiode égale à 5.10-4mol, comme déjà indiqué dans mon message du 09-05-24 à 17:28.
Dans ton message du 09-05-24 à 17:50, tu évoques une dernière question où il serait question d'exponentielle... Peux-tu copier ici l'énoncé correspondant ?
le bon enonce est le suivant
On étudie la cinétique de synthèse de l'iodure d'hydrogène H2 + I2 → 2HI
Pour cela, on porte à 450°C quatre ballons numérotés 1; 2; 3 et 4 qui contiennent chacun un mélange réactionnel identique: 5.10-5 mol de I2 et 5,0.10-5 mol de H2.
Ces ballons sont maintenus à cette température pendant des durées t différentes puis brutalement refroidis
Le diode restant est dosé avec une solution de thiosulfate de sodium de concentration molaire
C 0,05 mol/L. On met quelques gouttes d'empois d'amidon.
1-) Quel est le rôle de l'empois d'amidon?
2- On a obtenu le tableau de résultats suivants (dosage du diiode en excès).
Ecrire l'équation-bilan de la réaction de dosage
étudié.
Compléter le tableau ci-dessus.
3-) Tracer le graphe n(I2) = f(t)
Echelle: 1cm pour 25 min; 1 cm pour 5,0.10-5 mol. Trouver la vitesse instantanée de disparition du diiode à la date t=0 puis à la date t = 100 min. Si la vitesse de disparition du diiode était constante et égale à sa valeur à la date t =0, quelle serait le nombre de mol de diiode dans le milieu réactionnel à la date t = 200 min ?
Dans ton message du 09-05-24 à 17:50, tu évoques une dernière question où il serait question d'exponentielle... Peux-tu copier ici l'énoncé correspondant ?
voici la question: Si la vitesse de disparition du diiode était constante et égale à sa valeur à la date t =0, quelle serait le nombre de mol de diiode dans le milieu réactionnel à la date t = 200 min ?
Merci d'avoir recopié proprement l'énoncé mais il contient manifestement une incohérence que tu as toi-même constaté en écrivant :
A t=0 on a n0=5.10-5mol a t=100 min j'ai n=3.425.10-4mol
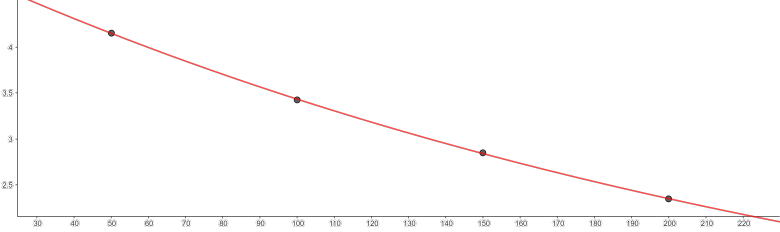
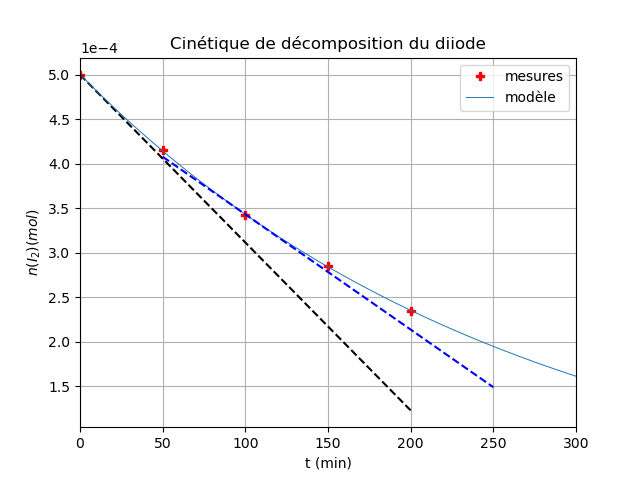
La quantité de I2 doit diminuer au cours du temps et pourtant, comme tu l'as calculé, les valeurs déduites du tableau de mesures sont supérieures à 5.10-5mol. Bref : l'énoncé contient une erreur quelque part. J'ai supposé le tableau de mesures sans erreur et j'ai corrigé la valeur initiale en 5.10-4 au lieu de 5.10-5mol. Voici ce que cela donne : ne pas oublier le facteur 1e-4=10-4 pour les graduations de l'axe vertical. J'ai ajouté les tangentes à la courbe en to=0 (pointillés noirs) et en t=100min (pointillés bleus).
Si la vitesse de disparition du diiode était constante et égale à sa valeur à la date t =0, quelle serait le nombre de mol de diiode dans le milieu réactionnel à la date t = 200 min ?
Cette question n'a rien à voir avec une exponentielle. Si la vitesse de disparition était une constante égale à la vitesse de disparition, la courbe n=f(t) serait une droite de coefficient directeur = -Vo : ce serait donc la ligne en pointillé noir déjà tracée...
je peux utiliser cette relation ?
Il se trouve qu'ici cette relation est correcte car nous avons une cinétique d'ordre 1 mais cela n'est pas indiqué dans l'énoncé et n'est pas, de toutes façons, au programme de terminale.
Le programme de terminale demande simplement d'exploiter la relation de définition de la vitesse :
Ce qui revient à considérer V comme l'opposé du coefficient directeur de la tangente à la courbe n(I2)=f(t).
Évidemment, avec si peu de points de mesures, cette méthode graphique est peu précise. Pour t'aider un peu, je t'ai tracé les deux tangentes utiles (pointillés noirs et bleus).
PS : j'ai utilisé un petit programme Python pour tracer les courbes mais il serait aussi possible d'utiliser un simple tableur : LibreOffice ou Excel par exemples.
Okey d'accord je vois
et si je devais utiliser la relation que j'ai proposé pour trouvé la valeur de k je peux remplacer par n'importe quel N (par exemple N a t=100 min ) pour sortir le k ou bien en posant V constant, ça change les valeurs des autres N ?
Pour trouver la valeur de k, sachant que No=5.10-4mol, tu peux prendre n'importe quel point à condition que celui-ci soit soit sur la courbe moyenne. Existe aussi, sur tableur ou ici sous Python, des programmes dit de "régression" qui tiennent compte de tous les points et calculent la courbe moyenne passant au plus près des divers points. J'ai obtenu ainsi k=3,77.10-3min-1 mais ici, c'est la méthode des tangentes qui est recommandée niveau terminale.
Effectivement, en supposant V=Vo, on obtient n(I2) 1,25.10-4mol alors qu'en réalité, la vitesse instantanée de réaction diminue au cours du temps ; on obtient n(I2)
1,25.10-4mol alors qu'en réalité, la vitesse instantanée de réaction diminue au cours du temps ; on obtient n(I2) 2,35.10-4mol .
2,35.10-4mol .
PS : attention à ne pas oublier les unités !