Inscription / Connexion Nouveau Sujet
Cinétique
Bonsoir à tous,
C'est la fin des vacances, et bientôt le début de la prépa... Il s'agit donc de me remettre les idées en place avant cette rentrée, aussi j'aimerais quelques éclaircissements sur un exercice, si vous voulez bien m'aider.
Voici l'énoncé:
On étudie, en milieu acide, la réaction d'oxydation suivante:
2H3O+ + 2I- + H2O2 = I2 + 4H2O
On cherche à comprendre l'influence de la concentration en H2O2 sur la vitesse de la réaction.
On place pour cela dans un bécher:
- 150mL de H2SO4 à 0.2molL-1.
- 10mL de (K+, I-).
- quelques goutes d'empois d'amidon
La concentration de la solution d'eau oxygénée utilisée est 0,5molL-1.
On place dans la burette une solution de thiosulfate de potassium (2Na+, S2O32-) à 1molL-1. On fait couler 0.5mL de cette solution dans le bécher.
A t=0, on verse 10mL d'eau oxygénée dans le bécher.
Lorsque la couleur vire au bleu, on note le temps t1 et on ajoute immédiatement 0.5mL de thiosulfate, on note ainsi les temps ti d'apparition de la couleur bleue pendant environ 90min.
Le di-iode formé réagit avec les ions thiosulfates selon la réaction rapide (devant la réaction étudiée) et quantitative suivante : I2 + 2S2O32- = 2I- + S4O62-
1) Nombre initial de mol de H2O2?
2) Combien y a-t-il de moles de thiosulfate dans 0.5mL de la solution?
3) Quelle relation lie le nombre de moles de S2O32- versé et le nombre de moles de H2O2 consommés? En déduire l'expression numérique du nombre de moles de H2O2 restant en fonction de ti.
Pour la suite j'ai une courbe représentant la concentration de H2O2 en fonction du temps, et cette question:
Ajouter au tableau une colonne de calcul de la vitesse à l'aide de la formule (à justifier) vi = ([H2O2]i-1-([H2O2]i+1)/(ti+1-ti-1). Tracer v en fonction de [H2O2], en déduire que v peut s'écrire : v = k [H2O2], déterminer k, précisez son unité.
Voilà, pour l'instant j'en suis là:
1) Je ne comprend pas vraiment... L'eau oxygénée n'est mentionnée qu'au début, ensuite on a uniquement l'indication sur la concentration...
2) n = c*v = 1*0.5 .10-3 = 0.5 .10-3 mol
3) Ici je ne vois pas... Je ne sais pas si, suivant la démarche de l'exercice, il s'agit de logique par rapport à ce qui est consommé et ce que l'on verse à chaque fois ou s'il faut utiliser un tableau d'avancement... Dans les deux cas je ne trouve rien.
Merci d'avance à ceux qui voudront bien m'accorder un peu de leur temps.
Salut  !
!
1) Tu as toutes les équations, donc tu sais à quoi est corrélée la valeur de la concentration en utilisant les tableaux d'avancement.
2) et comment en arrives-tu à cela?
3) C'est ce dont je te parlais pour la question 1)  Utilise un tableau d'avancement et les équations aux équivalences
Utilise un tableau d'avancement et les équations aux équivalences 
Salut, merci pour ta réponse rapide.
Je crois que je me suis trop laissé perturbé par le côté atypique de l'exo.
C'est une sorte de dosage indirect?
1) Pourtant dans la première équation, je n'ai aucun moyen de connaitre le réactif limitant ni même les autres quantités initiales de moles. Il faut combiner les deux équations? Dans ce cas là je coince... Je ne comprend pas l'intérêt du H2SO4 qui n'intervient dans aucune des deux réactions...
2) Je suis peut être aller un peu vite en pensant qu'il s'agissait de la solution de la burette... Il s'agit du bécher? Je dois utiliser la même méthode que plus haut?
Oui et ce n'est même pas une sorte à mon goût 
1) Milieu acide favorisant la réaction
2) je te demande simplement d'être plus rigoureux(se)
1) Les ions H3O+ sont en excès, oui, mais je ne connais que le volume d'I- et uniquement la concentration en H2O2
2) Autant pour moi (rigoureux :p). Ca me paraissait évident, c'est pour ça que je suis passé vite... la solution de thiosulfate est à 1mol.L-1, donc dans 0.5mL, ça va de soi il me semble...
Je suis en train de chercher pour la question 3.
Désolé si je suis un peu lent à la détente, c'est toujours un peu dur après 2 mois de vacances...
1) Cherche avec l'équivalence et travaille avec les volumes. Tu n'as pas beaucoup de choix ici.
2) Tout à fait, mais il convient de le préciser (même l'évidence, tu verras qu'en prépa c'est comme ça) 
tu es loin d'être long à la détente (surtout que je n'arpente que sporadiquement le forum contrairement à toi) et c'est déjà une intention très louable de se remettre à jour dans l'optique de la prépa (de nombreux futurs taupins sont loin de ces préoccupations je peux te l'assurer).
Quelle filière?
1) Avec l'équivalence, d'accord! Donc normalement, à l'équivalence il y a changement de réactif limitant.
2I-- xf = 0 et H2O2 - xf = 0
Soit 2I- = H2O2 et je retombe sur le manque de données... Je suis à peu près sûr qu'il faille utiliser cette donnée -
150mL de H2SO4 à 0.2molL-1.
2) Merci pour l'info, je ferais attention.
Je rentre en prépa intégrée dans le cadre d'une école d'ingénieur, ça se rapproche fortement du MPSI.
Attention ce ne sont pas les éléments qui sont égaux mais les quantités de matière ou les concentrations si tu fais le tableau en concentrations! Et là si tu disposes d'au moins un volume tu as l'autre et donc... La quantité de matière
2) je t'en prie, plus tu seras rigoureux mieux ce sera
Ok, tu veux intégrer quelle école si ce n'est pas indiscret?
Oui, je parle en quantité de matière, je l'ai écris de cette manière sur le forum pour plus de lisibilité, j'aurais du le préciser.
Je ne comprend pas, on nous dit que l'on utilise un bécher de 250mL mais pas qu'on le remplit jusqu'au bout, je ne peux pas déduire d'un premier volume l'autre volume...
Je viens de voir une info que j'avais complètement zappé:
on verse 10mL d'eau oxygénée dans le bécher.
Au final avec la concentration de 0.5 mol.L-1 je ne devrais même pas avoir à faire tout ça, et j'y vais comme pour la question suivante...
Pour la question 3, je dois résonner à l'équivalence dans les deux équations?
J'ai oublié de répondre à ta question: je rentre à l'ISEN.
1) Donc (sans rédiger sur le forum ^^) n(H2O2) = c * v = 0.5 * 10 .10-3
3) Voilà mon raisonnement.
A l'équivalence n(H2O2) = xf = n(I2)
Et n(I2) = 2n(S2O32-)
D'où n(H2O2) = 2n(S2O32-)
Ok, en revanche pour la deuxième partie de l'exo je sèche complètement. Comment lier ti à cette relation?
Le I- disparait donc du I2 apparait, donc on ajoute 0.5mL de thiosulfate qui réagit avec l'I2 pour reformer du I-... Je suis un peu perdu
J'ai mes deux tableaux d'avancement devant moi... (On parle bien de la 2eme partie de la question 3?)
Si je suis le raisonnement de la question, je devrais à partir de ça
n(H2O2) = 2n(S2O32-)
être capable de trouver la suite... Pourtant je ne vois vraiment pas où implanter ce ti
Oui oui on parle bien de la même
Il faut que tu définisses un x dépendant de t... à toi de trouver de qui il s'agit
A un t donné je rajoute du thiosulfate... Je suppose donc que ce x est lié à la quantité de matière de thiosulfate. Puisqu'on rajoute 0.5mL à chaque t, je dirais n(S2O32-) = c * 0.5t ?
Ca me parait faux...
Décidément je rame avec un bout de bois ^^'
Pourtant si on travaille à l'équivalence je ne peux pas utiliser le x de l'avancement de la réaction? Si je devais trouver un x, comme j'ai dit ce serait le nombre de mol de thiosulfate puisque c'est le paramètre que l'on modifie en ajoutant à chaque fois 0.5mL...
Une pagaie est aussi un morceau de bois à part si tu considères les nouvelles ultra-modernes utilisées pour les JO... mais ici on ne prépare pas les JO désolé 
Et bien oui c'est bien ça... Donc tu peux utiliser ton x
Je voulais dire que j'avais l'impression de ramer avec une brindille plutôt qu'avec une pagaie 
Donc j'ai n(H2O2) = 2x
Mais il me reste à déterminer l'expression de x en fonction de t. Et c'est là que je sèche, ce que j'ai proposé deux réponses auparavant ne peut décemment pas être juste...
J'aimerais que tu détailles l'ensemble de ton raisonnement parce-que j'avoue avoir du mal à cerner ton problème 
S'il-te-plaît 
Alors:
Quelle relation lie le nombre de moles de S2O32- versé et le nombre de moles de H2O2 consommés?
A l'équivalence
On a, dans la première réaction n(H2O2) - xf = 0 d'où n(H2O2) = xf
De même n(I2) = xf
D'où n(H2O2) = n(I2)
Si ensuite on se penche sur la deuxième équation, on a, toujours à l'équivalence:
2n(S2O32-) - xf = 0
n(I2) - xf = 0
D'où n(I2) = 2n(S2O32-)
En combinant tout ça on tombe sur la relation
n(H2O2) = 2n(S2O32-)
En déduire l'expression numérique du nombre de moles de H2O2 restant en fonction de ti.
Il faut donc, comme tu me l'as fait remarqué que je pose x = n(S2O32-) (en fonction du temps)
Or il faut que je trouve, justement, une formule où je peux caser une variable "t", si j'ai bien compris la question. Et je ne vois pas comment faire intervenir cette variable dans cette équation
n(H2O2) = 2n(S2O32-)
On a, dans la première réaction n(H2O2) - xf = 0 d'où n(H2O2) = xf
le reste du raisonnement est correct

Je t'avoue que je ne comprend pas...
xf se distingue bien du x que j'ai défini plus haut, non? Dans ce cas que dois-je remplacer?
Et si je remplace n(H2O2) je suis en dehors de la question, puisque je dois trouver une expression incluant au moins n(H2O2) et ti
Je pense que c'est sur ce point que je bloque. Pourtant à chaque temps t la couleur vire au bleu, c'est donc que l'état d'équilibre est atteint à chaque fois non?
Si je remplace tout de même xf par x je n'ai toujours pas d'expression incluant t...
Bien sûr il y a plusieurs équilibres. x dépend déjà de t  (c'est une fonction, donc x s'exprime en fonction de t)
(c'est une fonction, donc x s'exprime en fonction de t)
Bonjour,
Problème classique de dégénérescence d'ordre d'Ostwald.
La vitesse de la réaction :
2H3O^(+) + 2I^(-) + H2O2 --> I2 + 4H2O
est étudiée en fixant d'une part la concentration de l'ion H3O^(+) (excès d'acide) et d'autre part celle de l'ion I^(-) (en ajoutant l'ion SO3^(2-) qui réagit rapidement sur l'espèce I2 pour régénérer l'ion I^(-) selon 2SO3^(2-)+I2-> S4O6^(2-)+2I^(-)) ==>n(I2)=n(SO3^(2-) . La vitesse de la réaction ne dépend alors que de la concentration de H2O2 qui varie dans le temps. On mesure les temps successif nécessaires à la consommation d'une même quantité de H2O2 qui vaut : n(H2O2)=n(SO3^(2-)/2).
1---------
0.5*0,01=5*10^(-3) mol
2---------
1*0.0005=5*10^(-4) mol
3---------
n(H2O2)=n(SO3^(2-))/2
n(H2O2)(ti)=n(H2O2)(0)-i*(n(SO3^(2-))/2)
n(H2O2)(ti)=5*10^(-3)-i*2.5*10^(-4)
4---------
Les variations de volume peuvent être négligées
d(n(H2O2))/dt≈(n(H2O2)i-1-n(H2O2)i+1)/(ti+1-ti-1)=n(SO3^(2-)/(ti+1-ti-1)
v(t)=d[H2O2]/dt≈n(SO3^(2-)/(V*(ti+1-ti-1))
s^(-1) est l'unité de k
Bonsoir,
Désolé pour la réponse quelque peu tardive, j'étais très occupé aujourd'hui.
@Shadowmiko: Il est évident oui que x dépend de t, mais la question n'impose-t-elle pas d'elle même qu'un t soit introduit dans la formule? Ou du moins quelque chose avec i...
@Barbidoux: Merci tout d'abord pour tes éclaircissements sur le sens général de l'exercice, je pense l'avoir mieux cerné désormais.
Cependant (Je passe pour les questions 1 et 2 qui sont finalement relativement simples) pourrais tu détailler la question? Je ne comprend pas en particulier pourquoi tu arrives à
n(H2O2)=n(SO3^(2-))/2
n(H2O2) = 2n(S2O32-)
De même, par quel raisonnement arrives-tu à la relation finale? Plus que de finir l'exercice, il s'agit surtout pour moi de comprendre ^^'
De même tu es un peu rapide pour moi à la question 4

Petit problème de frappe dans mon précédent message il faut lire
2SO3^(2-)+I2-> S4O6^(2-)+2I^(-)) ==>n(I2)=n(SO3^(2-))/2 (stoechiométrie de la réaction)
2H3O^(+) + 2I^(-) + H2O2 --> I2 + 4H2O ==> n(I2)=n(H2O2) (stoechiométrie de la réaction)
d'où :
n(H2O2)=n(SO3^(2-))/2
-----------
4---------
La variation du nombre de moles de H2O2 entre deux lecture du temps est constantes et égale à la moitié du nombre de mole d'ion thiosulfate ajoutées (n(H2O2)=n(SO3^(2-))/2) (réaction sui régénère en continu l'espèce I^(-) dont la concentration reste constante au cours du temps) et ti+1-ti est le temps nécessaire à la réaction pour consommer ce nombre de moles.
La vitesse de réaction se calcule numériquement en ti comme la dérivée numérique de la courbe [H2O2]=f(t) soit
v(t)=d[H2O2]/dt≈(n(H2O2)i-1-n(H2O2)i+1)/(ti+1-ti-1)=n(SO3^(2-))/(V*(ti+1-ti-1))
Salut Barbidoux,
Pour la question 3 je suis sûr que tu dois avoir raison, cependant pourquoi, à l'équivalence on a bien n(I2) - xf = 0 et 2n(S2O3(2-)) - xf = 0
D'où n(I2) = 2n(S2O3(2-)) ?
Pourrais-tu également, si ça ne te dérange pas m'expliquer cette ligne
n(H2O2)(ti)=n(H2O2)(0)-i*(n(SO3^(2-))/2)
Pour la question 4, je pense avoir compris, cependant si j'ai bien justement bien compris tu vas plus loin que la question non?
n(SO3^(2-))/(V*(ti+1-ti-1))
Salut Barbidoux,
Il reste certaines choses que je ne comprend pas...
Pour la question 3 je suis sûr que tu dois avoir raison, cependant pourquoi, à l'équivalence on a bien n(I2) - xf = 0 et 2n(S2O3(2-)) - xf = 0
D'où n(I2) = 2n(S2O3(2-)) ?
Pourrais-tu également, si ça ne te dérange pas m'expliquer cette ligne:
n(H2O2)(ti)=n(H2O2)(0)-i*(n(SO3^(2-))/2)
……..2SO3^(2-).......+.........I2....... -> S4O6^(2-)+2I^(-))
t.....(n(SO3^(2-))-2x)......(n(I2)-x)..........(x).......(2x)
Conditions stoechiométriques n(SO3^(2-))/2=(n(I2) et n(S4O6^(2-))=n(I^(-))/2
---------------
La variation ∆n(H2O2) du nombre de moles de H2O2 consommées entre deux lecture du temps est constantes et égale à la moitié du nombre de mole d'ion thiosulfate ajoutées (n(H2O2)=n(SO3^(2-))/2) (réaction 2SO3^(2-)+I2-> S4O6^(2-)+2I^(-)) régénère en continu l'espèce I^(-) dont la concentration reste constante au cours du temps) ce qui fait que :
n(H2O2)(ti)=n(H2O2)(0)-i*∆n(H2O2)=n(H2O2)(0)-i*(n(SO3^(2-))/2)
Salut,
Merci bien pour tes explications, c'est beaucoup plus clair maintenant!
Désormais si je veux calculer le nombre de mole de H2O2 qu'il reste en fonction du temps passé j'utilise
n(H2O2)(ti)=n(H2O2)(0)-i*(n(SO3^(2-))/2)
et si je veux la concentration, je n'ai qu'à divisé le tout par le volume? Mais quel volume dois-je choisir?
Ok ok, merci à tous les deux pour votre aide, ça va beaucoup mieux maintenant.
Il me reste juste à trouver comment faire ça...
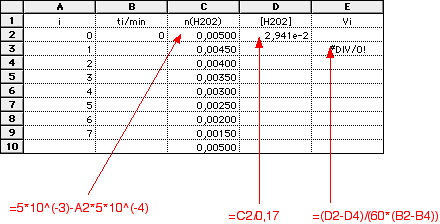
Ajouter au tableau une colonne de calcul de la vitesse à l'aide de la formule
J'ai très rarement utilisé Excel donc j'en ai vraiment aucune idée ^^'