1) Deux grandeurs X et Y sont proportionnelles s'il existe un nombre k constant tel que Y = kX
Exemple : Pour un mouvement uniforme la distance parcourue est proportionnelle à la durée.
Ici la distance parcourue D ne peut pas être mise sous la forme D = kt
Si la durée est multipliée par 2, 3 , ou 4 la distance parcourue n'est pas multipliée par 2, 3, ou 4

2) Il faudrait pour cela nager à une vitesse de 10km/h par rapport à l'eau dans une direction opposée à celle du courant.
Il faut donc être bien entrainé et de toutes manière on ne tiendra pas le coup bien longtemps !

3) Le module de l'accélération est le rapport entre la variation de module de la vitesse et la durée de cette variation.

4) Le module de l'accélération centripète est égal à V²/R
Plus on est près du centre, plus R est petit, plus le module de l'accélération est grand.

Bonjour,

Ok pour les trois dernières propositions.
Si j'ai bien compris pour que deux grandeurs soient proportionnelles, il faut une constante de proportionnalité, c'est ça? Et une constante de proportionnalité c'est une valeur qui ne varie pas, qui est donc bien constante?

Oui
Si tu achètes X kg de carottes et que tu paies P euros alors P et X sont des grandeurs proportionnelles parce que :
P = k*X

k est une constante qui est ici le prix de 1 kg de carottes
Si X est multiplié par 2, 3 ou 4 alors P est multiplié par 2, 3 ou 4

Bien entendu, dans cet exemple la valeur de la constante k peut changer .... le lendemain !

Mais alors, dans tout ce qui est MRU, MRUA, MCU, MCUA, il n'y a pas vraiment de constante de proportionnalité, si?

Ah oui, et en fait, je ne suis pas d'accord avec la question 2.

Si la rivière a un courant de 5km/h et imaginons nous on nage aussi à 5km/h mais dans une direction opposée à celui de la rivière, dans ce cas la vitesse résultante sera 0 k/h. Comment on pourrait arriver à 5km/h ?

2. Il me semble cependant que, si on nage dans une certaine direction avec une vitesse égale à celle du courant, la vitesse résultante peut elle aussi être égale à cette vitesse.

Effectivement !
Je n'ai pas été assez attentif aux conditions posées par l'énoncé (égalité des 3 modules des trois vitesses)

Donc par exemple pour x(t) = xo + vo*t, ça c'est une équation horaire de MRU. Dans un MRU, le mobile va parcourir des distances égales dans des intervalles de temps égaux. C'est donc proportionnel, mais ou est la constante de proportionnalité ici?

x(t) = xo + vo*t .
La distance parcourue pendant le temps  t , c'est  x(t) - xo  et on a  x(t) - xo = vo*t .
Elle est bien proportionnelle au temps.

Ok merci.

Je reviens sur la proposition 2 qui concerne le nageur.
La réponse que j'avais faite (19-03-19 à 11:02) ne convient pas puisque l'énoncé impose que les trois vitesses doivent être égales à 5km/h et que j'avais proposé une solution dans laquelle la vitesse du nageur était de 10km/h

Je te joins un schéma montrant une solution dans laquelle on a les trois vitesses de même module et qui satisfait la relation :
Vitesse du nageur par rapport à la rive = Vitesse du nageur par rapport au courant + vitesse du courant par rapport à la rive soit en langage mathématique :

                                  

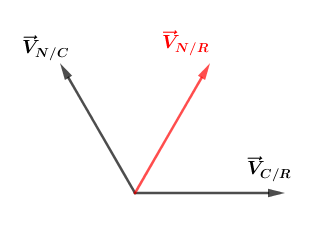
Ces trois vitesses sont de meme modules donc toutes les trois valent 5km/h? Mais alors, c'est possible que dans cette direction la?

Oui, la direction prise par le nageur doit faire un angle de 120° avec celle du courant.

Ah oui, c'est comme si on disait que nous avons trois forces concourantes et on cherche la force résultante?
Mais dans ce cas, on arriverait à une force résultante de 0N... j'ai rien dit

Ce que tu dis n'est pas idiot !

La relation         pourrait aussi bien s'écrire      

D'accord, donc comme dans l'énoncé ce n'est pas précisé dans quelle direction on se dirige, ça sous-entend qu'on peut faire un angle de 120° comme les forces concourantes?

Il n'y a aucun sous entendu.
La seule manière pour le nageur d'obtenir le même module pour les trois vitesses est de nager dans une direction formant un angle de 120° avec celle du courant.

Oublie ta comparaison avec les forces, elle risque de t'embrouiller au lieu de t'aider.

D'accord.

Mais peut on généraliser maintenant ou bien c'est cas par cas?
Peut-on dire qu'en formant un angle de 120°, ça conserve le meme résultat?

Il faut toujours être très prudent quand on cherche à généraliser.

Toutefois, ici, si le nageur décide d'adopter une vitesse égale à celle du courant (pas forcément 5 km/h) et de nager dans une direction formant un angle de 120° avec le courant alors les 3 vitesses auront la même norme.

Bonjour,

Je bloque encore sur la proposition 2.
Comment vous avez su trouver  qu'en formant un angle de 120 ° les trois vecteurs pouvaient avoir la meme norme?

Regarde la figure.
Tu y repèreras des triangles équilatéraux dont les angles sont tous égaux à 60°
L'angle cherché entre la vitesse du courant par rapport à la rive et la vitesse du nageur par rapport au courant est égal à la somme de deux angles de 60° soit un angle de 120°

Je pense que je ne comprends pas quand vous dites : "vitesse du courant par rapport à la rive". Pourquoi vous faite un rapport entre la vitesse du courant et la rive?

Relis mon post du  20-03-19 à 08:48