Inscription / Connexion Nouveau Sujet
Cinématique dépassement et croisement
Bonjour tout le monde, veuillez m'assister svp.
Exercice
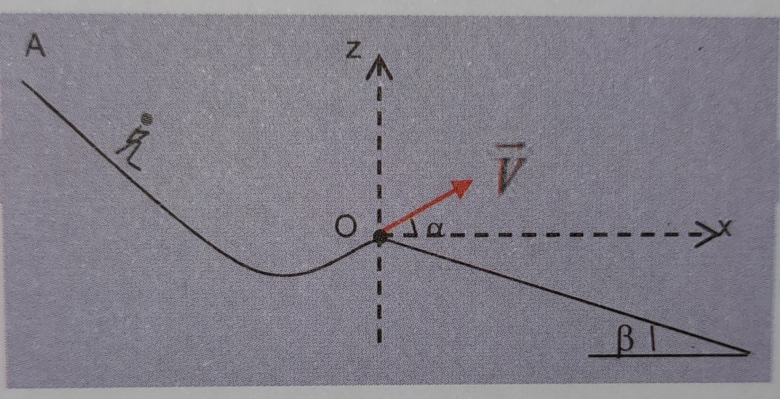
Un skieur de masse m = 80 kg s'élance sur une piste d'appel et parvient à l'extrémité O du tremplin incliné, faisant un angle avec l'horizontale, avec une vitesse de 72 km/h. On néglige la résistance de l'air et on prendra g = 10 SI. (Figure)
1) Écrire l'équation de la trajectoire du skieur au-delà du point O. On assimilera le skieur à un point matériel.
2) Donner l'expression de la longueur l = OB du saut mesurée sur la piste de réception.
La piste de réception fait avec le plan horizontal un angle de réception de = 45⁰.
3) Quelle inclinaison 0 faut-il donner au tremplin pour obtenir le saut le plus long pour une vitesse donnée du skieur au passage en O et une inclinaison
de la piste ?
1) Équation de la trajectoire au-delà du point O
- système : skieur de masse m ;
- référentiel : terrestre (supposé galiléen) ;
- bilan des forces appliquées : le poids du skieur.
Application du Théorème du centre d'inertie :
Soit
Dans le repère (Ox, Oz), on a :
Les coordonnées du vecteur accélération sont :
Les coordonnées du vecteur vitesse sont :
(VOcos
; - gt + VOsin
)
Les coordonnées du vecteur position sont :
(Vocos
t ; - ½gt² + Vosin
t)
En éliminant le temps entre les coordonnées du vecteur position on obtient l'équation de la trajectoire :
Z = -
AN :
Z = -
En remarquant que 1/cos² = 1 + tan²
, on obtient :
Z = -
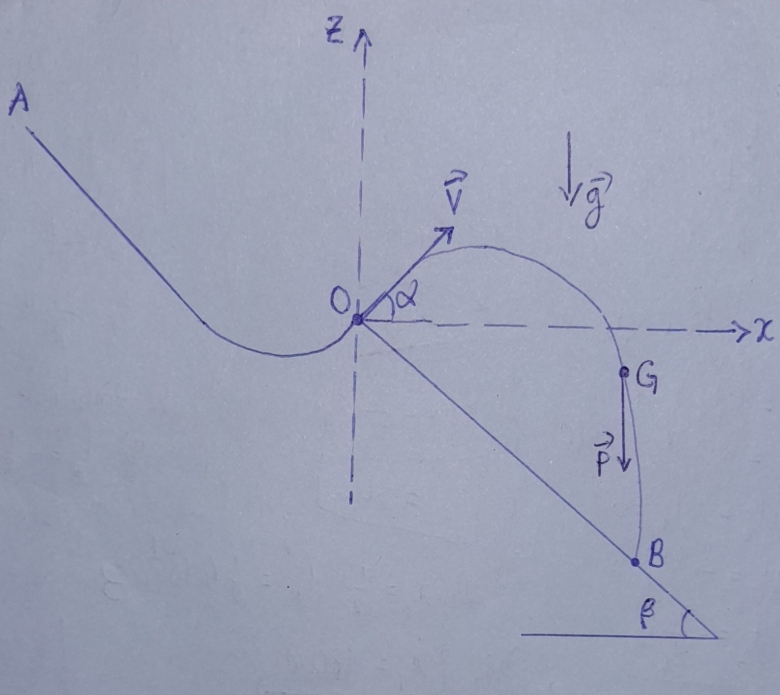
2) Expression de l = OB
La droite (OB) est de la forme Z = aX + b
Où a = -tan(45⁰) = -1 la pente et b = 0 l'ordonnée à l'origine.
Soit Z = -X
Or en B, la droite (OB) et la parabole à la question 1) ont même ordonnée.
Alors je pose :
En simplifiant X partout, on obtient :
Soit : XB =
Le point B étant sur la droite (OB) alors ZB = - XB = -
Sur la figure : OB² = Z²B+X²B
Alors :
3) valeur 0 de
pour que OB soit maximale :
Là, j'avoue que je n'ai rien compris.
J'ai posé (sans être sûr) : OB est max si 1 + tan >= 0
Donc 0 = 45⁰
La valeur α0 de la variable α qui rend OB maximale est l'une de celles qui annule la dérivée
de OB par rapport à α
Quand je dérive OB par rapport à j'obtiens une équation qui m'est impossible de trouver la racine.
Voici ce que j'ai trouvé en dérivant OB par rapport à
Je ne trouve pas le même résultat que toi.
Pour alléger la rédaction je pose :
OB = L et
L'expression de OB devient :
et par dérivation j'obtiens
D'accord, je vois.
Maintenant
Je trouve
Ou
Donc 0=67,5⁰
L'autre solution est à rejeter parce qu'elle est < 0, n'est-ce pas ?
J'ai trouvé des résultats opposés aux tiens :
α0 = 22,5° et
α0 = - 67,5° à rejeter car l'angle cherché est positif



