Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Cinématique

Posté par
Xenoverse 23-07-25 à 16:31

Bonjour j'ai besoin d'aide sur l'exercice merci.
exercice

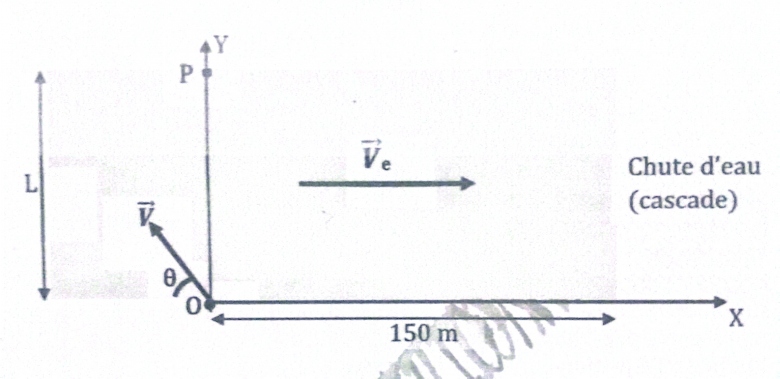
1.Un homme veut traverser un fleuve de largeur L:l'eau coule uniformément
à la vitesse constante Ve par rapport aux rives supposées rectilignes et auxquelles est associé le repère (R). L'homme nage à la vitesse constante \vec{V} faisant un angle \theta avec les rives.

1.1. Exprimer le vecteur vitesse \vec {V }du nageur dans le repère (R) en fonction de Ve et V.

1.2 Quelle est en fonction de L et V la durée de la traversée ?
1.3 Quelle direction doit prendre son corps par rapport aux rives pour faire la traversée en un temps minimal ?

2. Maintenant on suppose que le nageur part d'un point O et veut arriver au point P se trouvant sur l'autre rive directement-opposé à O en nageant au maximum- Quelle doit être la relation entre V et Ve pour que cela soit possible?

3. On suppose que Ve> V
3.1 Quelle direction doit prendre son corps pour arriver sur l'autre rive à l'endroit le plus proche de P.
On donne L = 50m; V = 100 m/min; Ve=5 m/s.

3.2 Si le point O d'où plonge le nageur est situé à 150 m d'une cascade. Pourra-t-il arriver à traverser le fleuve avant la chute d'eau ?

Cinématique

Posté par
vanoisere : Cinématique 23-07-25 à 17:04

Bonjour
Peut-être une étourderie de copie de ta part : si  V désigne la vitesse du nageur par rapport à l'eau, la vitesse du nageur par rapport à la terre doit avoir une autre notation : Va peut-être, comme vitesse absolue ?
Tu dois connaître la relation de composition des vitesses (un peu juste à mon avis en terminale) :

\vec {V_a} = \vec V +\vec{V_e}
Commence par faire un schéma propre représentant ces trois vecteurs. Il te sera alors possible de répondre aux questions posées.

Posté par
vanoisere : Cinématique 23-07-25 à 17:57

Tant que tu n'auras pas éclaircis cette histoire de notation concernant la vitesse par rapport à la terre (les berges), je ne peux pas avoir d'avis très tranché mais tout de même, cet exercice ne me semble pas du tout du niveau terminale et est nettement plus délicat que ceux que tu as posés précédemment. Cet exercice provient d'un livre de terminale ou tu l'as trouvé sur le net ? Cela m'étonnerait qu'il puisse avoir été donné par un professeur de terminale...

Posté par
vanoisere : Cinématique 23-07-25 à 18:19

Je viens de trouver un énoncé quasi identique sur un site destiné aux étudiants de niveau (Bac+1) - (Bac+2)...

Posté par
Xenoversere : Cinématique 23-07-25 à 18:26

Bonsoir, effectivement c'est un exercice de terminale s et je l'est trouvé dans mon livre oui effectivement je connais la composition des vitesses et c'est exprimer Vn du nageur dans le repère.... C'est une erreur de ma part

Posté par
vanoisere : Cinématique 23-07-25 à 19:14

OK mais cet exercice est à mon avis plus difficile que celui sur le rayon de courbure au sommet d'une parabole.
Il faut donc poser :

\vec {V_n} = \vec V +\vec{V_e}

puis considérer que la trajectoire du mouvement par rapport aux berges est un segment de droite dirigé par le vecteur \vec {V_n}
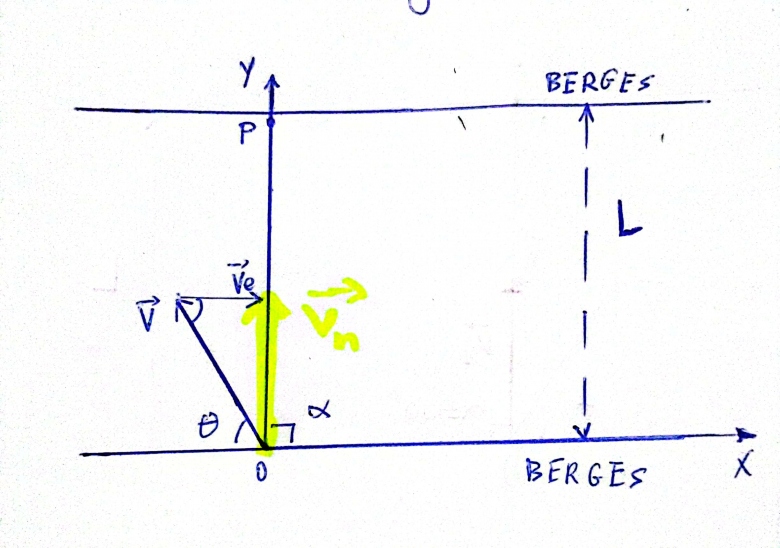
Je te laisse proposer un schéma propre de la situation dans le cas général.

Posté par
Xenoversere : Cinématique 23-07-25 à 23:15

OK me revoilà donc : \vec{V_n}=\vec{V}+\vec{V_e} \rightarrow \vec{V_n}=(Vcos\theta+V_e)\vec{i} + Vsin\theta\vec{j}
Ensuite 1.2 la durée de la traversée.

Posté par
Xenoversere : Cinématique 23-07-25 à 23:24

J'ai ma petite idée ; on nous dit dans l'exercice que Ve est constante et V aussi donc \vec{V_n}=constante+constante \rightarrow V_n=constante ( MRU) X(t) et y(t) ? X(t)=0 regardez mon schéma ensuite je cherche t dans y(t) . Si c'est bon on continue.

Cinématique

Posté par
Nico299re : Cinématique 24-07-25 à 05:39

***Intervention supprimée, non conforme au règlement***

Posté par
vanoisere : Cinématique 24-07-25 à 08:52

@Nico299
Je crois que tu n'as pas bien lu le règlement ; l'usage sur ce forum est de laisser le premier aidant intervenu guider l'élève jusqu'au bout de l'exercice. D'autres aidant peuvent bien sûr intervenir en cas d'erreur ou en fin d'exercice pour proposer des méthodes alternatives. Cela évite certaines dérives constatés sur d'autres forums où un grand nombre d'aidants potentiels interviennent sans toujours (souvent... avoir lu tous les messages précédents, ce qui crée la confusion.
@Xenoverse
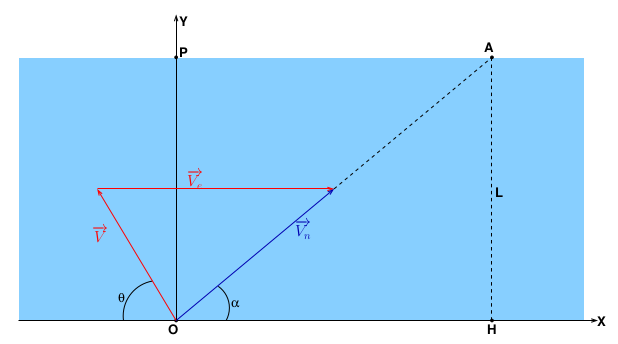
Ta figure est correcte physiquement mais ne respecte pas la définition de fournie par l'énoncé. Pour la première question, le rapport Ve/V est quelconque. Je l'ai choisi plus grand que 1 ; ainsi ma figure pourra servir aux questions 1 et 3. Tu aura intérêt à refaire une figure pour la question 2. Pour la question 1, projeter la relation vectorielle de composition des vitesses suffit .

Cinématique

Posté par
vanoisere : Cinématique 24-07-25 à 09:05

@Nico299
Je te laisse lire cet extrait du règlement, en particulier le paragraphe 1 de la partie intitulée :
Aux membres aidant sur le forum :
[***A LIRE AVANT D'AGIR***] Règles du forum

Posté par
gbm Webmasterre : Cinématique 24-07-25 à 09:53

Bonjour à tous,

@Nico299 : tu es nouveau sur le forum, bienvenue ! Comme indiqué par vanoise dans son dernier message, tu as des règles de bienséance à respecter. Je t'invite donc à lire attentivement cette synthèse de la FAQ.

Posté par
vanoisere : Cinématique 24-07-25 à 12:01

Petite précision à propos de l'énoncé de la question 1 :
question 1.2 : dans le cas général, la durée de traversée t dépend de L, de V et de .
Question 1.3 : il faut trouver la valeur de qui rend t minimum à L et V données.

Posté par
Xenoversere : Cinématique 24-07-25 à 12:09

Bonjour pourquoi je dois faire un autre schéma pour la question 2 et je dois y mettre quoi ?

Posté par
vanoisere : Cinématique 24-07-25 à 13:24

La question 2 correspond au cas particulier =90°. Un schéma analogue au précédent adapté à ce cas particulier peut aider...

Posté par
vanoisere : Cinématique 24-07-25 à 14:21

Pour la détermination de t , plusieurs méthodes sont possibles ; je te propose une méthode assez simple, bien adaptée me semble-t-il au niveau terminale. Le repère d'étude est le repère (O,X,Y) lié à la terre.
Puisque, comme tu l'as écrit précédemment, le mouvement dans ce repère est rectiligne uniforme, tu as immédiatement :

\triangle t=\dfrac{\text{distance parcourue}}{\text{vitesse}}=\dfrac{OA}{V_{n}}

Un minimum de trigonométrie concernant le triangle rectangle (OAH) permet d'exprimer la distance OA en fonction de L et de .

Ensuite, la projection selon (OY) de la relation vectorielle de composition des vitesses donne une relation très simple entre V, sin(), Vn et sin(al).

En tenant compte de tout cela, tu obtiens l'expression demandée de t en fonction de L, V et .

Posté par
vanoisere : Cinématique 24-07-25 à 14:23

avant dernière phrase : "relation entre V, sin(), Vn et sin()"

Posté par
Xenoversere : Cinématique 24-07-25 à 16:33

Mais ici alpha n'est pas égal à 90° et t'a dit sa dans ton message de 13h 24

Posté par
Xenoversere : Cinématique 24-07-25 à 16:37

😅 non oubliez ce que j'ai dit j'ai confondu un truc.

Xenoverse @ 24-07-2025 à 16:33

Mais ici alpha n'est pas égal à 90° et t'a dit sa dans ton message de 13h 24

Posté par
vanoisere : Cinématique 24-07-25 à 16:46

Pour la question 1.2 , il faut utiliser la figure correspondant au cas général : celle du  24-07-25 à 08:52. Commence par résoudre la question 1 avant de te préoccuper de la question 2. Je t'ai détaillé la méthode dans mon message de 14h21.

Posté par
Xenoversere : Cinématique 24-07-25 à 17:33

Mais pourquoi on ne fait pas une projection sur (OX)?

Posté par
vanoisere : Cinématique 24-07-25 à 18:37

tu as une autre méthode que tu peux utiliser si la précédente te parait inhabituelle. Le mouvement étant rectiligne uniforme de vitesse \vec {V_n} = \vec V +\vec{V_e}, les équations horaires du mouvements sont :
x=Vnx.t
y=Vny.t
où Vnx et Vny sont les deux composantes du vecteur \vec{V_n}
La durée de traversée est ainsi la date tA d'arrivée en A donc la date correspondant à y=L.
C'est donc la projection de la relation de composition des vitesses selon (Oy) qui est particulièrement utile pour la question 1.2.

Posté par
Xenoversere : Cinématique 24-07-25 à 18:43

Non là n'est pas la question si je comprenais pourquoi on ne projette pas suivant (OX) j'aurais pu continuer là dessus

Posté par
vanoisere : Cinématique 24-07-25 à 19:13

L'abscisse du point A étant pour l'instant inconnue, utiliser la projection sur (Ox) donc la relation x=Vnx.t ne renseigne pas sur la durée de traversée égale à tA.
PS : Nous sommes d'accord : il s'agit toujours de répondre à la question 1...

Posté par
Xenoversere : Cinématique 24-07-25 à 19:18

Oui il s'agit de la question 1 mais je ne sais pas ou vous voulez en venir,

Posté par
vanoisere : Cinématique 24-07-25 à 21:37

Pour commencer : as-tu bien compris la figure que je t'ai envoyée ce matin à 8h52 ? Si non, pose des questions précises à son sujet.
Ensuite : question 1.1 : c'est tout simplement la relation de composition des vitesses :

\vec {V_n} = \vec V +\vec{V_e}
Tu m'as expliqué que cela ne posait pas de problème... Pose des questions tout de même en cas d'hésitation.

Question 1.2 où il faut trouver la durée du trajet OA : Je t'ai proposé à 14h21 une méthode utilisant la définition d'une durée d'un mouvement rectiligne uniforme. Tu m'as dit alors préférer une méthode utilisant la projection des vecteurs vitesse. Pas de problème : cette deuxième méthode est tout à fait utilisable et n'est pas très compliquée. Je t'ai détaillé cette méthode dans mon message de 18h37. As-tu compris ce message ? Si non, pose des questions précises... Quand je t'ai parlé en préambule d'exercice difficile au niveau terminale, je pensais surtout à la question 3...

Posté par
Xenoversere : Cinématique 24-07-25 à 22:17

Ok ma question c'est tu me demande de projeter suivant  oy et de laisser la projection suivant OX alors le vecteur Vn a aussi bien une composante suivant x que suivant y n'est-ce pas ? dans la formule delta t on a la norme Vn or sa norme égal \sqrt{x²+y²} c'est ça en Grosso modo

Posté par
vanoisere : Cinématique 24-07-25 à 23:03

Attention : \Vert\overrightarrow{V_{n}}\Vert=\sqrt{V_{nx}^{2}+V_{ny}^{2}} mais, si on utilise la méthode des projections, il n'est pas nécessaire de déterminer cette norme.

La projection de la relation de composition des vitesses sur les deux axes conduit à :

V_{nx}=V_{e}-V.\cos\left(\theta\right)\qquad;\qquad V_{ny}=V.\sin\left(\theta\right)

Tu suis pour l'instant ? En posant t=0 à l'instant où le nageur part du point O :

x=\left[V_{e}-V.\cos\left(\theta\right)\right].t\quad;\quad y=V.\sin\left(\theta\right).t

La durée de la traversée est la durée du trajet rectiligne OA donc la date tA d'arrivée en A.

L'abscisse de A est inconnue alors que l'ordonnée est connue : y_{A}=L. On va donc raisonner sur l'ordonnée pour calculer tA. Ainsi la réponse à la question 1.2 est :

\boxed{t_{A}=\frac{L}{V.\sin\left(\theta\right)}}

Pour la question 1.3, il faut considérer L et V comme deux constantes et comme une variable. Dans l'expression de tA, pour diminuer le quotient, il faut augmenter le dénominateur. Pour rendre tA minimum, il faut rendre le dénominateur maximum, donc choisir :

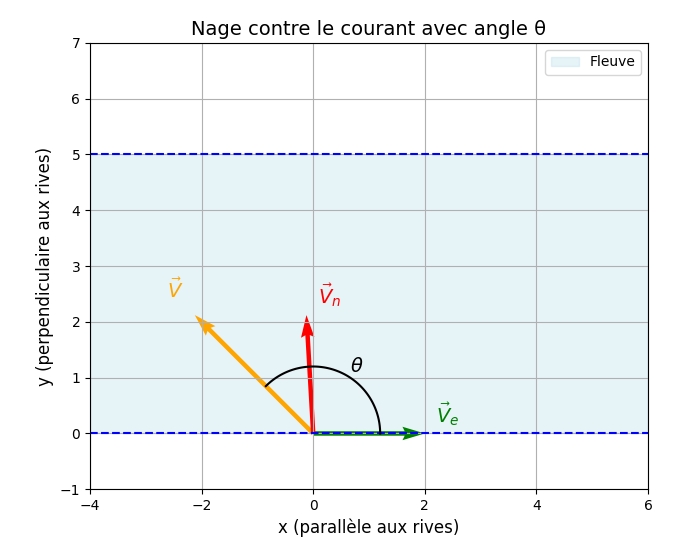
\sin\left(\theta\right)=1 soit \theta=90{^\circ}. Le nageur doit maintenir son corps perpendiculaire aux berges, perpendiculaire à l'axe (Ox). Évidemment, à cause du courant, il va dériver vers la droite et atteindre la berge en un point A conformément à la figure ci-dessous donnée à titre d'illustration et valide seulement dans ce cas particulier d'une durée minimale de traversée.

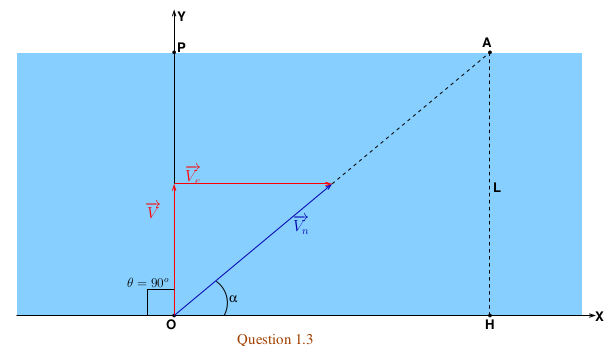
Cinématique

Posté par
Xenoversere : Cinématique 25-07-25 à 02:18

Question 3,  on doit compenser la dérive du courant pour que le nageur arrive au point P , pour ça il faut que la composante horizontal soit nulle, V_e-Vcos\theta=0 \rightarrow cos\theta=\frac{V_e}{V} or pour que cos(theta) existe il faut -1\leq cos\theta\leq1 équivaut à -1\leq\frac{V_e}{V}\leq1 \rightarrow \boxed{V_e\leq V}

Cinématique

Posté par
Xenoversere : Cinématique 25-07-25 à 09:50

Bonjour,3-1) on a \frac{V_e}{V} \geq1 \rightarrow cos\theta \geq1 donc il n'existe pas d'angle de compensation pour arriver pile à P pour le nageur donc pour arriver à un point le plus proche de P vu qu'il subit le courant donc ça va dépendre du temps mis donc le temps doit être minimum et T(traversée )minimale si sin\theta minimum donc \boxed{\theta}=90°
3-2) \boxed{X(traversée)=147m} donc le nageur ne va pas se casser la figure pour de bon.

Posté par
Xenoversere : Cinématique 25-07-25 à 09:56

Bonjour,3-1) on a \frac{V_e}{V} \geq 1 \rightarrow cos\theta \geq 1  impossible ,donc il n'existe pas d'angle de compensation pour arriver pile à P pour le nageur donc pour arriver à un point le plus proche de P vu qu'il subit le courant donc ça va dépendre du temps mis donc le temps doit être minimum et T(traversée )minimale si sin\theta minimum donc \boxed{\theta=90°} il doit orienter son corps perpendiculairement aux berges.
3-2) \boxed{X(traversée)=147m} donc le nageur ne va pas se casser la figure pour de bon.

Posté par
Candidere : Cinématique 25-07-25 à 11:59

Bonjour,

Revois tes réponses à la question 3.

theta = 90° correspond au temps de traversée minimum ... mais pas à la dérive minimum

Posté par
vanoisere : Cinématique 25-07-25 à 14:03

Ton message du  25-07-25 à 02:18 :
S'il concerne la question 2 et non la question 3 : d'accord à une remarque près. Il faut écrire <90° et Ve<V. En effet, dans le cas : \vec {V_n} = \vec V +\vec{V_e}=\vec 0. Le nageur fait du "sur place" par rapport à la terre. Il reste en 0 et n'atteint jamais la berge opposée.
Concernant la question 3 : mon message du 24-07-25 à 23:03 devrait beaucoup t'aider. Il s'agit dans un premier temps d'obtenir l'expression générale de la dérive : OP=xA, abscisse à la date tA d'arrivée en A. Or, je t'ai fourni l'expression générale de x et tu connais tA...
Ensuite, puisque Ve et V sont des grandeur fixes, il faut considérer cette dérive comme une fonction de la variable : xA=f().
Il faut procéder comme en mathématique, la variable étant plutôt que x. Il te faut calculer la dérivée par rapport à : f'() puis remplir un tableau de variation comme en math.
Pour cela, il va te falloir te souvenir des dérivées d'un sinus et d'un cosinus, ainsi que de l'expression générale de la dérivée d'un quotient de deux fonctions de :
[cos()]'=...
[sin()]'=...

\left(\dfrac{u}{v}\right)^{,}=...

Posté par
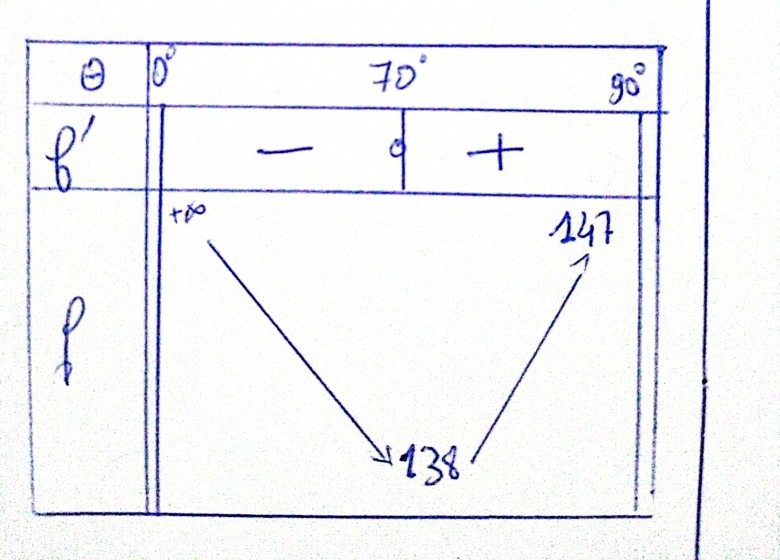
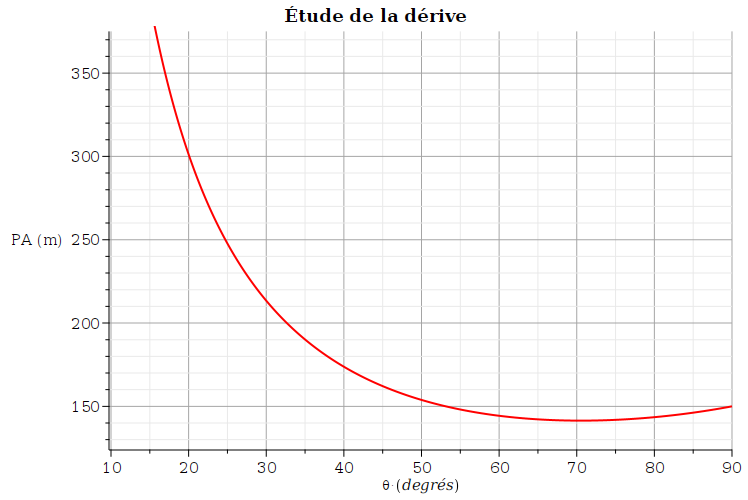
vanoisere : Cinématique 25-07-25 à 14:04

Je me suis mal relu : la dérive est la distance PA=xA

Posté par
vanoisere : Cinématique 25-07-25 à 14:57

Pour t'autocorriger, voici la courbe représentant les variations de la dérive PA=xA en fonction de ]0,90°[.

Cinématique

Posté par
vanoisere : Cinématique 25-07-25 à 15:34

imprécision dans mon message de 14h03 à propos de la question 2.
Il faut écrire >0° et Ve<V. En effet, dans le cas =0 : \vec {V_n} = \vec V +\vec{V_e}=\vec 0. Le nageur fait du "sur place" par rapport à la terre. Il reste en 0 et n'atteint jamais la berge opposée.

Posté par
Xenoversere : Cinématique 25-07-25 à 19:42

Bonjour, bon je ne comprends pas pourquoi je dois mettre theta>0° alors qu'on m'a juste demandé la relation entre Ve et V pour rendre l'arrivée en P possible je crois si c'était en devoir j'aurai le point d'ailleurs l'inégalité doit être large (≥) au lieu de (>) car -1\leq cos\theta\leq1 pourrait tu détailler un peu sur ça et aussi j'avoue que j'ai pas trop compris ce que je dois faire pour la question 3 -1) mais je crois que si je me réfère attentivement à tes explications je pourrais avancer

Posté par
Xenoversere : Cinématique 25-07-25 à 20:41

Bon, là j'ai creusé pendant longtemps mais rien ne vient j'ai absolument rien compris pour résoudre la question 3 -1 c'est le flou total.

Posté par
vanoisere : Cinématique 25-07-25 à 21:04

Il faut réfléchir au sens physique des formules. Considère le cas =0 : le vecteur V est orienté suivant (-Ox) et le vecteur Ve est toujours orienté suivant (+Ox). La somme des deux vecteur (vecteur Vn) est donc nécessairement orienté suivant 0x, selon que V est supérieure ou inférieure à Ve. Conséquence : la composante Vny est toujours nulle, le nageur n'atteindra jamais la berge opposée ! Cela est d'ailleurs cohérent avec la formule démontrée pour la durée de traversée :
\boxed{t_{A}=\frac{L}{V.\sin\left(\theta\right)}}
Pour 0, tA : le nageur n'atteint jamais la berge.
Pour la question 3 : je t'avais prévenu ! Mais enfin, en s'accrochant un peu :
je t'ai fourni l'expression générale de x :
x=\left[V_{e}-V.\cos\left(\theta\right)\right].t
Je viens de te rappeler l'expression de tA ; il suffit de remplacer t par tA dans l'expression générale de x pour avoir xA=PA : la distance dont le courant a fait dériver le nageur.
La suite : il s'agit de mathématique et j'ai détaillé les calculs à faire en fin de mon message de 14h03... Pose des questions précises sur ce qui te bloque.

Posté par
Xenoversere : Cinématique 25-07-25 à 22:10

Oui le souci c'est que j'ai calculé la dérivée de f(\theta)=X_a=85-\frac{cos\theta}{1,7sin²\theta} mais son signe me pose problème il faut que je sache son signe pour tracer le tableau de variation de f(\theta) c'est ça mon problème.

Posté par
Xenoversere : Cinématique 25-07-25 à 22:47

Bon j'y suis. Au final on a ça :

Cinématique

Posté par
vanoisere : Cinématique 25-07-25 à 22:52

Remarque préliminaire : il est préférable de raisonner littéralement : cela permet à chaque étape de vérifier l'homogénéité des formules obtenues et ainsi d'éviter des erreurs grossières...   Comme expliqué dans mon précédent message, l'expression de la dérive est :

PA=x_{A}=\left[V_{e}-V.\cos\left(\theta\right)\right].t_{A}=\frac{L}{V}\cdot\frac{V_{e}-V.\cos\left(\theta\right)}{\sin\left(\theta\right)}

L/V étant une constante dans le calcul de la dérivée par rapport à , on le sort de la dérivation :

\frac{dx_{A}}{d\theta}=\frac{L}{V}\cdot\left[\frac{V_{e}-V.\cos\left(\theta\right)}{\sin\left(\theta\right)}\right]^{'}=\frac{L}{V}\cdot\left(\frac{u}{v}\right)^{'} \\
En posant : u=V_{e}-V.\cos\left(\theta\right) et v=\sin\left(\theta\right)

Cours de math :

u'=V.\sin\left(\theta\right) ; v'=\cos\left(\theta\right)

\frac{dx_{A}}{d\theta}=\frac{L}{V}\cdot\frac{u'.v-v'.u}{v^{2}}=\frac{L}{V}\cdot\frac{V.\sin^{2}\left(\theta\right)-\cos\left(\theta\right).\left[V_{e}-V.\cos\left(\theta\right)\right]}{\sin^{2}\left(\theta\right)}

Sachant que : \cos^{2}\left(\theta\right)+\sin^{2}\left(\theta\right)=1 :

\frac{dx_{A}}{d\theta}=\frac{L}{V}\cdot\frac{V-V_{e}.\cos\left(\theta\right)}{\sin^{2}\left(\theta\right)}

On voit que la dérivée de xA par rapport à s'annule pour :

\cos\left(\theta\right)=\frac{V}{V_{e}}

On voit bien que cette formule n'a de sens que pour V<Ve comme précisé dans l'énoncé puisqu'ici le cosinus est strictement inférieur à 1. Je te laisse remplir un tableau de variation pour 0<\theta\leq90{^\circ} pour montrer que la valeur nulle de la dérivée correspond à un minimum de xA et non à un maximum.

Je te laisse faire les applications numériques...

Posté par
vanoisere : Cinématique 25-07-25 à 22:59

Je viens de voir ton message de 22h47 après avoir posté mon message précédent. Tu as vraiment fait tous les calculs ou tu t'es contenté de valeurs approximatives déduites de la courbe fournie ?
Si on fait les calculs rigoureux pour arrondir ensuite à 3 chiffres significatifs comme cela se fait souvent, on n'obtient pas tout à fait tes résultats...

Posté par
Xenoversere : Cinématique 25-07-25 à 23:12

Non j'ai même pas regardé votre courbe j'ai creusé comme un vrai scientifique et déterminer les intervalles où f' est>;<et=0 puis tracer le tableau c'est juste que les valeurs tombent à peu près juste..

Posté par
Xenoversere : Cinématique 25-07-25 à 23:20

Mais pour être franc je n'aurai jamais deviné qu'on doit passer par un tableau de signe et mon cerveau n'arrive pas à suivre votre compréhension des évènements et d'en déduire une route à tracer pour résoudre le problème et de votre compréhension physique des choses honnêtement j'en est terminé avec l'exo mais je ne suis pas satisfait car je veux être capable de faire un raisonnement rigoureux comme la vôtre dans d'autres exercices si non je risque de toujours m'en reposer aux autres.Des conseils ?

Posté par
Xenoversere : Cinématique 25-07-25 à 23:25

Moi je me pose toujours la question à savoir comment vous avez fait vous les professeurs pour en arriver à un tel niveau de compréhension.

Posté par
vanoisere : Cinématique 25-07-25 à 23:27

On obtient plus rigoureusement :
cos()=1/3 d'où 70,5° (pas grand mal effectivement)
(xA)min=2L2141m
Pour =90° : xA=3L=150m

Posté par
vanoisere : Cinématique 26-07-25 à 14:37

Citation :
Des conseils ?

Pour des raisons de prestige, certains livres et concepteurs d'énoncés posent des exercices de niveau bien supérieur à celui normalement exigé. Cela peut paraître perturbant et démoralisant pour les élèves et étudiants. Cet exercice ainsi que celui récent sur le rayon de courbure de la parabole sont habituellement donnés au niveau (bac+1).
Un conseil aussi : tu as toujours intérêt à raisonner sur des formules littérales. Le résultat est ainsi plus général (changer les valeurs numériques ne nécessite pas de refaire le problème) et surtout : il est possible de vérifier l'homogénéité des résultats au fur et à mesure. Si, par exemple, tu arrives à une formule où une accélération est égale à l'inverse d'une distance, c'est nécessairement que tu t'es trompé : des m/s2 ne peuvent être égaux à des m-1  !
Penser aussi à vérifier le réalisme des résultats obtenus. C'est en général assez simple en mécanique.

Posté par
Xenoversere : Cinématique 26-07-25 à 15:29

👍

vanoise @ 26-07-2025 à 14:37

Citation :
Des conseils ?

Pour des raisons de prestige, certains livres et concepteurs d'énoncés posent des exercices de niveau bien supérieur à celui normalement exigé. Cela peut paraître perturbant et démoralisant pour les élèves et étudiants. Cet exercice ainsi que celui récent sur le rayon de courbure de la parabole sont habituellement donnés au niveau (bac+1).
Un conseil aussi : tu as toujours intérêt à raisonner sur des formules littérales. Le résultat est ainsi plus général (changer les valeurs numériques ne nécessite pas de refaire le problème) et surtout...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 244 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !