Inscription / Connexion Nouveau Sujet
Cinématique
Bonjour j'ai besoin d'aide sur la question 1 ici on peut passer par deux chemins mais les résultats ne sont pas les mêmes premier chemin un peu passé par pente qui représente l'accélération la pente de la tangente deuxième chemin on peut passer par l'équation horaire de la vitesse
Vo=0 on trouve 0,6 il y a une incohérence voilà l'exercice
exercice
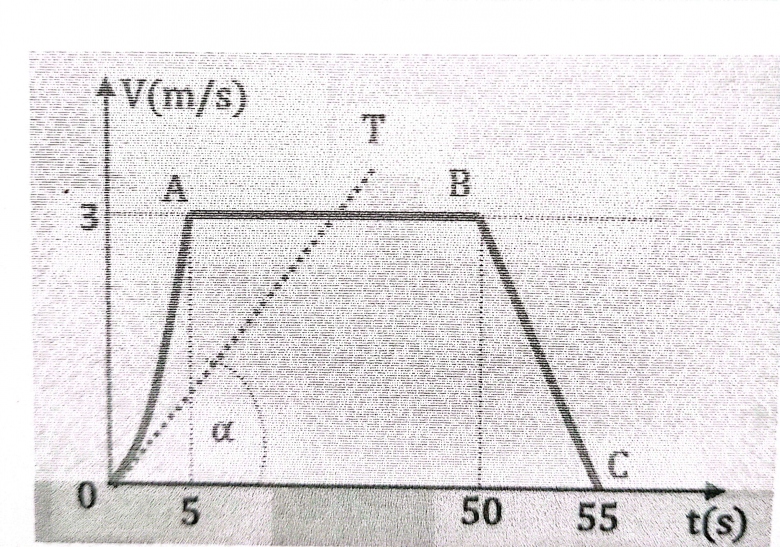
On donne ci-contre le diagramme de la vitesse d'un mouvement rectiligne.
.
OA est assimilable à une branche de parabole:
AB est une droite parallèle à l'axe des abscisses:
BC est un segment de droite;
OT est la tangente à l'origine du graphe représenté par OA; et on donne tan = 2/ 5
1) Déterminer l'équation horaire de la vitesse pour chaque phase.
2) Ecrire l'équation horaire de l'accélération pour chaque phase; représenter le diagramme de l'accélération.
Bonjour
Il faut passer par la tangente à la courbe ; son coefficient directeur est bien dv/dt = a l'accélération.
La branche OA est assimilable à une branche de parabole. Pour t<5s, on peut écrire :
v=p.t2+q.t
où p et q sont deux constantes que tu peux déterminer.
Tu peux alors obtenir l'expression en fonction de t de l'accélération et vérifier la cohérence du résultat avec l'accélération initiale déduite de la tangente.
Pourquoi on pourrait pas passer par cette méthode de l'équation horaires c'est plus facile pour moi.
deuxième chemin on peut passer par l'équation horaire de la vitesse
l'équation v=a.t correspondant à un mouvement uniformément varié correspondrait à un segment de droite entre O et A. Or, on obtient une branche de parabole d'équation générale :
v=p.t2+q.t dans la mesure ou v=0 si t=0.
En dérivant, tu obtiens l'expression de l'accélération :
a=dv/dt=2p.t+q : l'accélération dépend de t.
La valeur de la tangente te fournit l'accélération initiale, donc la valeur de q. Tu obtiens la valeur de p en considérant que la branche de parabole passe par le point A.
Bonjour,
1) équation horaire de la vitesse pour chaque phase :
Phase OA: V(t)=pt^2+qt
a(t)=2pt+q
a(t) est obtenue en dérivant par rapport au temps V(t)
Nous connaissons ensuite 2 points de la courbe : (0;0) et (5;3)
De là nous obtenons p=1/25 et q=2/5
V(t)=(1/25)t^2+(2/5)t
Phase AB:
V(t)=3
Phase BC:
V(t)=ax+b
Nous lisons 2 points : (50;3) et (55;0)
Nous avons donc un système de 2 équations à 2 inconnues.
Les solutions de ce système donne a et b.
V(t)=-(3/5)t+33
2) équation horaire de l'accélération :
Phase OA:
a(t)=(2/25) t+2/5
Obtenue en dérivant par rapport au temps la vitesse.
Phase AB:
a(t)=0
Phase BC:
a(t)=-3/5
Bonjour Nico299
Pour aider sur ce forum, le règlement demande de ne pas fournir de corrigé "clé en main" mais simplement de fournir des indications pour aider l'élève à comprendre et à faire lui-même l'exercice. Ce n'est pas vraiment ce que tu as fait...
En plus, il s'agit d'un exercice de physique, pas de mathématique : toutes valeur numérique doit être fournie en nombre décimal avec une précision dépendant des données et toute valeur numérique non accompagnée de son unité, lorsque celle-ci existe, est considérée comme fausse...
En plus, ta méthode pour obtenir p et q n'est pas rigoureuse. Le fait que la branche de parabole passe par l'origine permet d'écrire l'équation de la parabole sous la forme : v=p.t2+q.t plutôt que sous la forme plus générale : v=p.t2+q.t+r puisque, si v=0 en t=0 : r=0.
C'est donc bien la valeur du coefficient directeur de la tangente à l'origine qui permet de trouver la valeur de q.
Bonjour Vanoise, y'a t'il une méthode plus rigoureuse pour déterminer q et p ?
En plus, ta méthode pour obtenir p et q n'est pas rigoureuse. Le fait que la branche de parabole passe par l'origine permet d'écrire l'équation de la parabole sous la forme : v=p.t2+q.t plutôt que sous la forme plus générale : v=p.t2+q.t+r puisque, si v=0 en t=0 : r=0.
C'est donc bien la valeur du coefficient directeur de la tangente à l'origine qui permet de trouver la valeur de q.
Je considère que la méthode de Nico299 n'est pas rigoureuse car il écrit :
“Nous connaissons ensuite 2 points de la courbe : (0;0) et (5;3) De là nous obtenons p=1/25 et q=2/5 “.
La branche de parabole passe par le point t=0,v=0 donc :
v=p.t2+q.t
En effet, si la parabole ne passait pas par ce point, il faudrait écrire :
v=p.t2+q.t +r
Autrement dit, le fait que la parabole passe par O ne fournit aucun renseignement sur les valeurs de p et q ; ce fait permet juste de poser r= 0 mais cela m'avait paru évident dès mon premier message... Il faut donc deux renseignements complémentaires pour obtenir les deux inconnues p et q.
Premier renseignement : l'accélération a pour expression générale :
a=dv/dt=2p.t+q
à t=0 : a=q = coefficient directeur de la tangente à la courbe v=f(t), donc :
q=0,4m/s2
Deuxième renseignement : la parabole passe par le point A :
La suite est facile !
Ce que je ne comprends pas c'est pourquoi l'accélération dépend du temps alors que le mouvement est rectiligne uniformément varié
Bonjour,
Nous pouvons remarquer que lors de la phase OA le mouvement n'est pas rectiligne mais suit une courbe d'où une accélération logiquement variable dépendante du temps. Nous pouvons d'ailleurs remarquer que sur cette courbe en chaque point la valeur de la pente est variable. Le mouvement n'est alors pas uniformément varié.
Ensuite lors des phases AB et BC nous avons des accélérations constantes d'où un mouvement uniformément varié.
le mouvement est rectiligne uniformément varié
Mais pour la phase OA, tu as v=p.t2+q.t , pas v=a.t ! Il n'y a pas que des mouvements uniformément variés dans la vie !
La phase BC correspond elle à un mouvement uniformément varié (uniformément retardé pour être plus précis). La phase AB correspond elle à un mouvement uniforme puisque la vitesse est fixe.
Bonjour,
Nous pouvons remarquer que lors de la phase OA le mouvement n'est pas rectiligne mais suit une courbe d'où une accélération logiquement variable dépendante du temps. Nous pouvons d'ailleurs remarquer que sur cette courbe en chaque point la valeur de la pente est variable. Le mouvement n'est alors pas uniformément varié.
Ensuite lors des phases AB et BC nous avons des accélérations constantes d'où un mouvement uniformément varié.
Bonjour,
C'est la représentation de la vitesse en fonction du temps qui n'est pas "rectiligne" sur le graphe.
Cela n'implique en rien la "forme" de la trajectoire... qui peut être rectiligne (et l'est, puisque c'est indiqué dans l'énoncé).
Par contre, le mouvement (bien que rectiligne) n'est ni uniforme (car vitesse non constante) ni uniformément varié (car accélération non constante).


