Inscription / Connexion Nouveau Sujet
Cinématique
Bonjour j'ai besoin d'aide sur la question 3 de l'exercice merci.
exercice
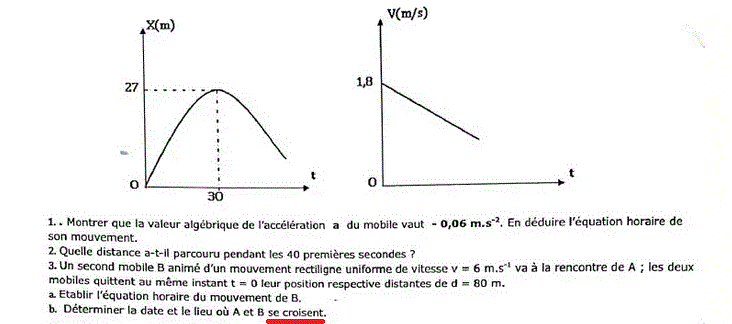
Un mobile A est animé d'un mouvement rectiligne uniformément varié. Les diagrammes de l' abscisse x(t) et de la vitesse v(t) sont donnés ci-dessous.
1) Quelle est l'accélération du mouvement ? En déduire l'équation horaire du mouvement.
2) Quelle distance a-t-il parcouru pendant les 40 premières secondes ?
3) Un second mobile B animé d'un mouvement rectiligne uniforme de vitesse v= 6m .s^-1 va à la rencontre de A les deux mobiles quittent au même instant t = 0 leur position respective distantes de d = 80m
a) Etablir l'équation horaire du mouvement de B.
b) Déterminer la date et le point où A rattrape B.
Bonsoir
La vitesse de B est positive : B se déplace vers la droite.
Il va à la rencontre de A : cela n'est possible que si xoB<0. D'ailleurs l'énoncé permet de calculer xoB puisque xoA=0 selon la courbe xA=f(t) fournie.
Si B provient de la gauche pour aller vers la droite et rejoindre A alors il y'a une incohérence dans la question suivante
b) Déterminer la date et le point où A rattrape B.
Mais aussi on peut considérer d'un autre côté que B provient de la droite et va à la rencontre de A car on a rien dit à se sujet dans l'exercice.
car on a rien dit à se sujet dans l'exercice.
Si B provenait de la droite, on aurait une vitesse de B négative.
b) Déterminer la date et le point où A rattrape B.
De toute les façons, cette phrase est illogique...
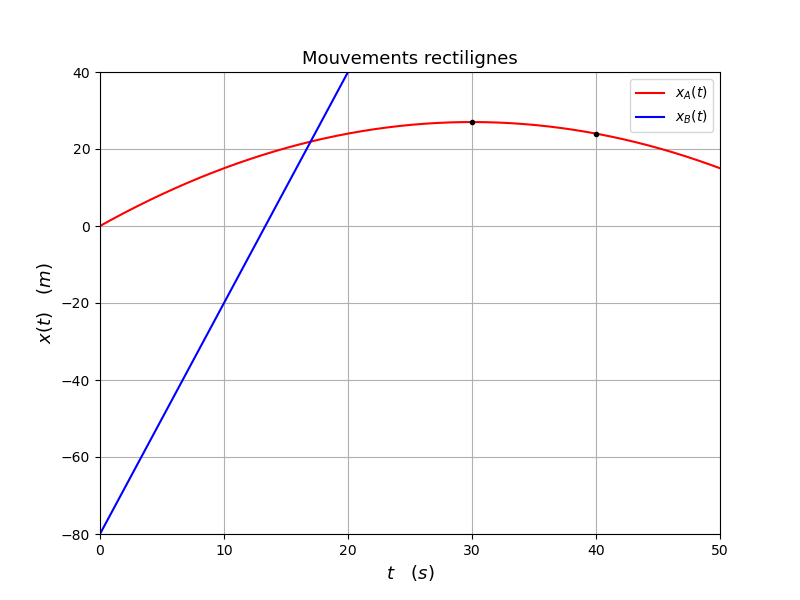
Supposons, comme je le pense, que B vient de la gauche : c'est B qui rattrape A. En effet, le calcul montre que la rencontre se produit pour t<30s, les deux vitesses sont toutes deux orientées vers la droite avec une vitesse de B nettement supérieure à celle de A (voir courbes ci-dessous).
Supposons, comme tu le penses que B provient de la droite. Il faut alors supposer deux erreurs dans l'énoncé :
1° : voB =-6m/s et non 6m/s (je suppose qu'il n'y a pas d'erreur sur la valeur absolue de cette vitesse) ;
2° : le calcul montre qu'alors les deux mobiles se croisent et non se rattrapent car la rencontre se produit pour t<30s, lorsque les deux mobiles ont des vitesses de sens opposés.
Deux erreurs : cela me paraît beaucoup. Il me semble donc plus vraisemblable de considérer l'absence d'erreur sur la vitesse de B puis une simple étourderie de permutation entre les lettres A et B dans l'énoncé de la question 3b).
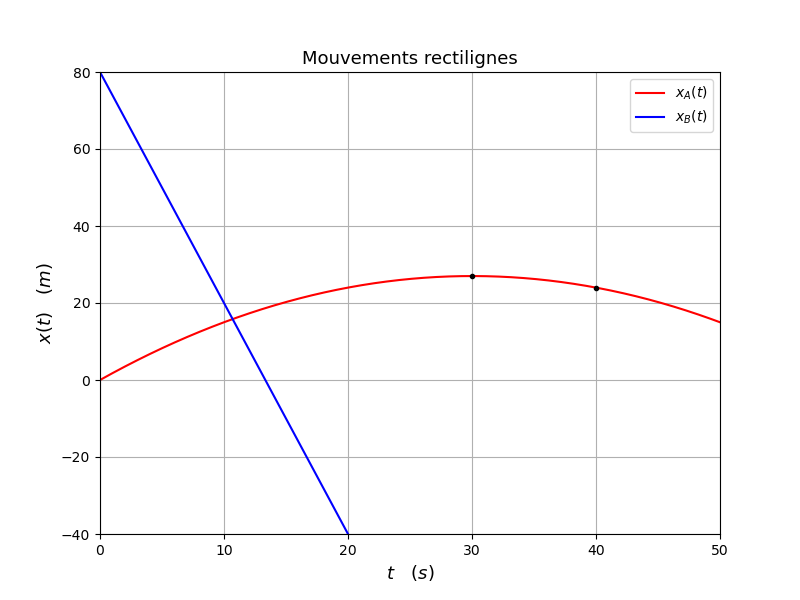
Pour bien illustrer les deux hypothèse sur le signe de la vitesse de B. Voici les courbes que l'on obtiendrait en imaginant B provenant de la droite. Les deux vitesses sont de sens opposés à l'instant où les deux mobiles se croisent (pas se rattrapent).
Bon, de toute façon peu importe le cas considérer notre raisonnement serait correct et je pense que si il n'y avait pas d'erreur je crois je n'aurai jamais eu à le posté donc merci pour ta vision globale des deux cas et on peut s'arrêter là de mon côté je vais considérer le premier cas un autre pour prendre l'autre l'essentiel c'est le raisonnement correct et rigoureux j'ai pas raison.
Bien sûr que tu as raison : c'est la qualité du raisonnement qui compte le plus. N'empêche que ce genre d'étourderie dans l'énoncé peut perturber un étudiant ou élève sérieux un jour d'examen ou de concours alors qu'un élève ou étudiant moins attentif ne verra pas la permutation entre A et B.
Bonjour,
Comme souvent, sur le net, les énoncés se recopient et les erreurs s'ajoutent aux erreurs dans les recopiage.
Il y en a cependant qui s'en rendent compte et corrigent, par exemple ici :
Ce nouvel énoncé est aussi incorrect si on veut être rigoureux. Il a été assez longuement démontré dans les messages précédents de Xenoverse et de moi-même que, avec les valeurs numériques fournies, la rencontre des deux mobiles se produit avec deux vecteurs vitesses de même sens, la vitesse de B étant supérieure à celle de A. C'est donc B qui rattrape A. On ne peut pas parler de croisement. Voir courbes fournies dans le message du 19-07-25 à 02:30...
Pas d'accord,
vA(t) = 1,8 + a * t (avec a < 0)
xA(t) = 1,8t + a*t²/2 (car xA(0) = 0)
27 * 1,8 * 30 + a * 900/2
a = -0,06 m/s²
vA(t) = 1,8 - 0,06*t
xA(t) = 1,8t - 0,03*t²
A t = 40 s, le mobile A se trouve à une distance d du point O,avec d = int(de0à40) (1,8 - 0,06*t) dt = 24 m
A cet instant vA(40) = 1,8 - 0,06 * 40 = -0,6 m/s (donc le mobile A va vers la gauche (et ce depuis t = 30 s d'ailleurs))
xB(t) = 80 - 6t (puisque distance initiale = 80 m et les mobiles vont, à l'origine de t, l'un vers l'autre (précisé en 3 de l'énoncé))
rencontre quand xA(t) = xB(t) --> 1,8t - 0,03*t² = 80 - 6t (avec t le plus petit)
---> t = 10,7 s (arrondi)
Point de rencontre à 80 - 6*10,7 = 15,8 m à droite de l'origine. (A cet instant, A va vers la droite et B vers la gauche ... c'est dont un "croisement" et pas un "rattrapage")
Où est alors ce qui n'irait pas dans l'énoncé du message du 19-07-25 à 10:44 ?
Le mobile A va vers la droite pour t dans [0 ; 30] s et vers la gauche pour t > 30 s. Le mobile B va en permanence vers la gauche.
Les mobiles sont au même endroit en t = 10,7 s donc ils se croisent.
Pas d'accord,
Merci de lire l'intégralité des messages précédents avant de poster un avis aussi "nuancé" !
L'hypothèse xoB=80m et voB=-6m/s a été testée dans le message du 19-07-25 à 02:30 et a été l'objet d'une représentation graphique dans le message du 19-07-25 à 02:38. Elle conduit bien à un croisement comme je l'avais indiqué alors. Cependant l'énoncé parle de vitesse de B égale à 6m/s et d'accélération de a=-0,06m/s2 ; ainsi l'énoncé algébriserait l'accélération mais pas la vitesse ?
Bref : il y a une ou plusieurs incohérence(s) dans cet énoncé et chacun peut les voir un peu où il veut. Comme dit par Xenoverse, l'essentiel est de faire un raisonnement cohérent, sans commettre de fautes grossières !

Cela dit, si j'avais eu sous les yeux hier l'énoncé du 19-07-25 à 10:44, j'aurais probablement privilégié l'hypothèse xoB=80m et voB=-6m/s par rapport à l'hypothèse xoB=-80m et voB=6m/s car ce dernier énoncé devient alors plus cohérent (il y a bien croisement) malgré le problème d'algébrisation de la vitesse.
Il y a aussi l'expression commune au deux énoncés : B "va à la rencontre de A ". Pour certains dictionnaires, cela signifie simplement que A et B se rapprochent. Pour d'autres comme l'encyclopédie Larousse, l'expression se limite à des situations où les deux se rapprochent avec des vitesses en sens inverses. Retenir cette définition plus restrictive donne clairement l'avantage à l'hypothèse : xoB=80m et voB=-6m/s illustrée par mon schéma du 19-07-25 à 02:38. Il n'y a plus qu'une seule incohérence d'énoncé ! 
"Retenir cette définition plus restrictive donne clairement l'avantage à l'hypothèse : xoB=80m et voB=-6m/s illustrée par mon schéma du 19-07-25 à 02:38. Il n'y a plus qu'une seule incohérence d'énoncé ! "
Il reste une seule incohérence dans l'énoncé initial ...
Mais comme je l'ai mentionné, il n'y a plus aucune incohérence dans l'énoncé du message du 19-07-25 à 10:44
Mon message de 16h35 à propos du dernier énoncé : "Cependant l'énoncé parle de vitesse de B égale à 6m/s et d'accélération de a=-0,06m/s2 ; ainsi l'énoncé algébriserait l'accélération mais pas la vitesse ? " Pour arriver à un croisement il faut poser v=-6m/s : là-dessus : tout le monde est d'accord !
Je m'arrête là ; comme déjà écrit : l'essentiel est de faire un raisonnement cohérent avec son interprétation de l'énoncé, sans commettre de fautes grossières !