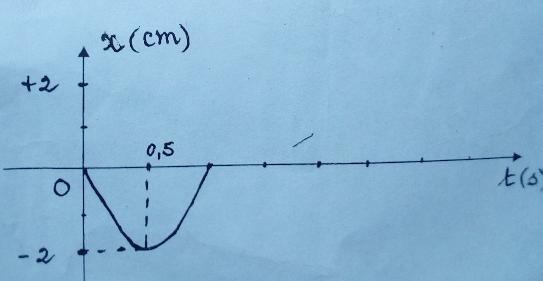
Bonsoir,

C'est une période particulièrement intense pour les correcteurs bénévoles, il ne faut pas hésiter à relancer en cas d'absence de réponse :

1. Où est la complétude du schéma reproduit ? Tu n'as pas une période et demi de représentée en l'état.

2. Effectivement, étant donné qu'à t = 0 s, x(0) = 0, l'équation horaire décrivant le mouvement du solide est une sinusoïde => es-tu en mesure de me la proposer ?

3. Utiliser l'équation horaire définie en 2.

voici comment moi j'ai fait la figure :
mais pour la question numéro 2 j'ai pas compris comment moi je vais faire puisque at = 0 seconde je sais pas la valeur de la vitesse initiale et de plus  je ne sais pas comment se fait-il que à tout=0 seconde et x0 = 0 . expliquer-moi comment faire s'il vous plaît

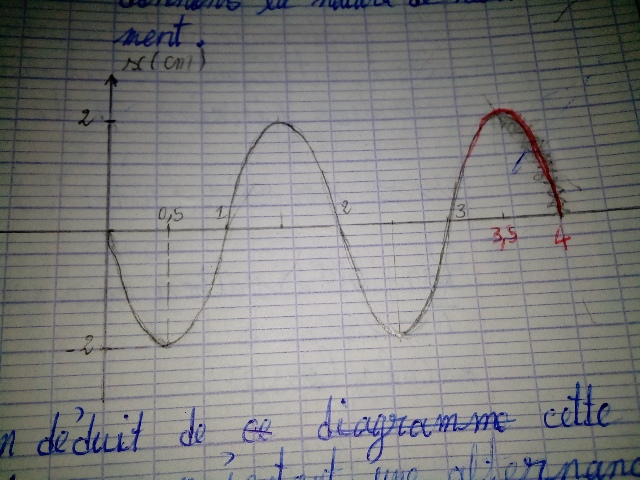
OK, d'après ton schéma, que vaut la période des oscillations ?

Est-ce qu'une courbe du style x(t) = A.sin(w.t) par exemple pourrait correspondre au mouvement ?

T= 2s , en ce qui concerne le schéma une courbe style x=Asin(wt+f) correspondera à son mouvement

Ok et donc ?

D'abord  je ne sais pas comment établir le poisson horaires de ce mobile

excusez-moi ce n'est pas le poisson horaires mais c'est l'équation horaire

Tu as reçu une aide précieuse de la part de krinn qui pourrait t'aider à te lancer dans cet exercice. Je te recommande de finir l'autre exercice avec lui, de te faire une fiche des principales notions révisées avec lui puis de revenir faire cet exercice pour qu'on en discute.

Il reste encore 2j avant la rentrée, c'est plus que jouable.

je ne sais pas comment procéder puisque :
à t=0s, x0= 0s et v0=?

Si x(t) = Xm.sin(wt + )

x(t) = 0 cm => Xm.sin() = 0

<=> sin() = 0

<=> = ?

Indice : réfère-toi à ton cours de mathématiques sur la trigonométrie.

Ensuite, w = 2/T = ... rad

sachant que T = 2s

alors w = ...

Enfin, l'élongation est maximale lorsque sin(wt + ) = 1, soit ici Xm = 2 cm

Donc l'équation horaire peut s'écrire ...

= π/2
w = π
xm = 0.02
l'équation horaire est donc :
x= 0.02sin{(π/2)t + π}

pour la question numéro 3 :

calculons t pour x = 0.01 m

0.01 = 0.02sin{(π/2)t + π}

=> 0.5 = sin{(π/2) + π}

=> 0.52  = (3/2)πt

=> 0.35 = πt
=> t = 0.11s donc la date du 5e  passage du mobile par le point d'abscisse égal à 1 cm est 5t = 0.55s

s'il vous plaît est-ce la bonne démarche que j'ai utilisé pour le calcul de la durée du 5e au passage du mobile?

Je ne comprends pas tout ce que tu as fait :

= π/2 unité ?
w = π unité ?
xm = 0.02 unité ?

l'équation horaire est donc :
x= 0.02sin{(π/2)t + π}

tu écris l'inverse de ce qui a été écrit plus haut (pour rappel x(t) = Xm.sin(wt + phi))

Sinon pour la question 3, ta démarche est correcte, reprends juste les applications numériques eu égard à l'inversion opérée en question 2

voilà l'équation
x= 0.02 sin(πt + π/2)

merci

Oui et donc ? As-tu fait une vérification de l'équation ?

Quid de la question 3 ?