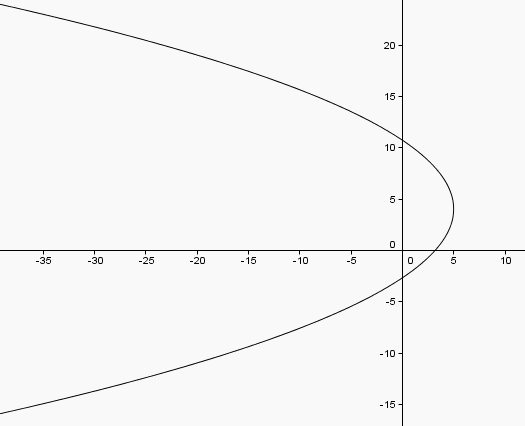Inscription / Connexion Nouveau Sujet
cinematique
bonjour !
Les composantes du vecteur vitesse d'un mobile en mouvement dans un plan muni d'un repere (o,i,j)sont Vx(t)=-2t+4 et Vy(t)=3
1)determiner les carcteristiques du vecteur accleration
2)a)determiner le vecteur espace sachant qu'a l'instant de date t=1s,le mobile passe par M(4,1) dans le repere(o,i,j)
b)chercher l'equation de trajectoire du mouvement et endeduire son nature
c)donner l'allure de cette trajectoire
3)a)donner les coordonnees du sommet S
b)en deduire le vecteur vitesse du mobile en S
pour le 1) direction:tangente a la trajectoire,sens : celui du mouvement,valeur: a = dv/dt,v(t)=(-2t+4)i+3j
a=-2i valeur de a racine de (-2)2=2m.s-2
2) V(t)=(-2t+4)i+3j,OM= v.dt=(-t2+4t+c1)i+(3t+c2)j
v.dt=(-t2+4t+c1)i+(3t+c2)j
OM(t=1)=4i+1j
(3+c1)i+(3+c2)j=4i+4j alors c1=1 et c2=-2
d'ou OM(t)=(-t2+4t+1)+(3t-2)j
????
aidez moi s'il vous plait je suis coince,je ne sais pas si c vrai ou faux,...
peut aussi s'écrire, en notant x et y les coordonnées du point M :
x(t) = -t2+4t+1
y(t) = 3t-2
Il faut maintenant que tu cherches l'équation de la trajectoire. Je te conseille une forme x(y)

oui j'ai fait comme ca puis je me suis arrete car je sentais qu'il y'a une faute quelque part : j'ai trouve t= (y+2)/3 puis j'ai remlace dans x(t)et j'ai trouve x(y)=(-y2+10y+29)/3
ce n'est pas faux ca ?
si c vrai comment je ferais pour faire l'allure et d'apres cette equation comment peut-on conclure la nature du mouvement ?
D'accord pour la méthode, mais je pense que tu as une erreur de calcul.
t = (y + 2)/3
mais recommence le calcul de x(y)...

oui oui je sais ....faute de frappe /9
mais apres comment je fais pour l'allure et comment peut conclure la nature du mouvement ?
Je suis sûr que si tu échangeais x en y et y en x tu saurais répondre. Or il n'y a aucune raison d'appeler un axe Ox plutôt que Oy et inversement.
Que proposes-tu ?

Je veux dire que si tu avais trouvé : y = (1/9)(-x2 +8x + 29)
Tu saurais répondre ; quelle est la courbe qui a une telle équation ?

La trajectoire est une parabole.
Son axe est parallèle à l'axe des abscisses (Ox) ; alors que tu as l'habitude de voir des paraboles dont l'axe est parallèle à l'axe des ordonnées (Oy)
Quant au mouvement il est clairement uniformément accéléré.
À la première question, tu as calculé l'accélération et tu as trouvé qu'elle ne dépend pas du temps : elle est constante. Donc : accélération constante = mouvement uniformément accéléré !
Question 3a
Facile de dessiner la parabole
Question 3b
Tu peux, comme l'énoncé le demande, "en déduire" la vecteur vitesse au sommet.
Tu peux aussi, en t'appuyant sur les résultats précédents (encore la première question ! ) et la réflexion, trouver immédiatement les coordonnées du vecteur vitesse au sommet de la parabole.

oui...j'ai pris mon gouter  maintenant je vois mieux ce que vous voulez dire...merci je vais dessiner la courbe puis je vous dirai si j'avais des problemes
maintenant je vois mieux ce que vous voulez dire...merci je vais dessiner la courbe puis je vous dirai si j'avais des problemes 
est ce que vous etes sur que la courbe que vous l'avez faites est juste ? ou ce n'est qu'un exemple pour me donner une idee ? sinon j'ai pas trouve comme vous ?
Equation de la trajectoire :
x = (1/9).(-y² + 8y + 29)
-----
Sommet de la trajectoire :
S(5 ; 4)
-----
vitesse en S:
t = (y+2)/3
t = (4+2)/3 = 2 s
Vx(2) = -2*2+4 = 0
Vy(2) = 3
|v| = 3 (en unités de longueur/s)
vecteur v : (0 ; 3)
-----
Sauf distraction. 
Je viens de profiter d'un peu de soleil (assez rare)...
_________
La courbe : oui, je suis sûr. Je l'ai tracée à partir de son équation paramétrique ET à partir de son équation cartésienne pour vérifier que les deux tracés se recouvrent...
Les coordonnées que tu proposes pour le sommet ne sont pas bonnes...
Une vitesse nulle ne peut pas être correcte (considère que Vy(t) = 3 : cette valeur ne dépend pas de t et est donc constante, jamais nulle...)
Désolé de ces réponses très négatives...
__________
Je te propose de commencer par la question 3b
Réflexion : que vaut Vx (la composante de la vitesse sur l'axe des abscisses) quand le mobile est au sommet de la trajectoire ?

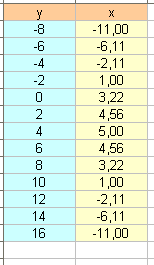
pour la courbe voila les valeur que j'ai pris :
y=-1,x=2,22 puis y=0,x=29/9; y=2 , x=4,55;y=3,x=3,11;y=4,x=5
J.P comment t'a fait pour trouver S(5,4) ?
ce n'est pas S(-b/2a,f(-b/2a)?
Bonjour J-P 
Étonnant : je suis sûr que ton message (18 h 05) n'était pas visible chez moi, quand j'ai posté le mien (18 h 11).
____________
hi-1995 >>
Si cela peut te rassurer, toutes mes réponses sont les mêmes que celles de J-P

oui mais mon probleme c'est que je ne sais pas comment dessiner la courbe, et determiner les coordonnees du sommet ?
ma demarche pour trouver la vitesse au sommet est la meme que JP donc y'a pas de probleme ici ! mais le probleme c'est que j'ai pas su comment faire la courbe et determiner les coordonnes de S ?
Je te propose, sans grand succès, une approche physique...
Que vaut la composante selon l'axe Ox (c'est-à-dire Vx) quand le mobile est au sommet de la trajectoire ?

Étonnant : je suis sûr que ton message (18 h 05) n'était pas visible chez moi, quand j'ai posté le mien (18 h 11).
Cela ne m'étonne pas, ce genre de problème m'est arrivé bien souvent aussi.
Je ne sais pas quelle en est la raison.
Peut-être un problème de cache ?


Je ne m'intéresse pas (encore) à la position du mobile mais à sa vitesse.
Avant le sommet Vx est positif : ce qui signifie que le mobile se déplace vers les x croissants
Après le sommet, Vx est négatif : ce qui signifie que le mobile se déplace vers les x décroissants
Quand il est juste au sommet de la trajectoire, le mobile a une vitesse dont la direction est celle de l'axe des ordonnées, Oy et la composante de la vitesse selon l'axe des abscisses est alors nulle
Vx(t) = -2t + 4 = 0
En conséquence, à quel instant t le mobile se trouve-t-il au sommet de la trajectoire ?

Mais oui ! !
Alors puisque tu sais que :
x(t) = -t2 + 4t + 1
y(t) = 3t - 2
Quelles sont les coordonnées x(2) et y(2) du sommet ?
Puisque tu sais que la vitesse a pour coordonnées :
Vx(t) = -2t + 4
Vy(t) = 3
Quelles sont les coordonnées du vecteur vitesse au sommet ?
Vx(2) = ...
Vy(2) = ...