Inscription / Connexion Nouveau Sujet
charge d'un condensateur
bonjour, j'ai cet exo à faire, j'aurais besoin d'un coup de main svp, merci.
On charge un condensateur de capacité C à l'aide d'un générateur de f.e.m. E et de résistance négligeable par l'intermédiaire d'une résistance R.
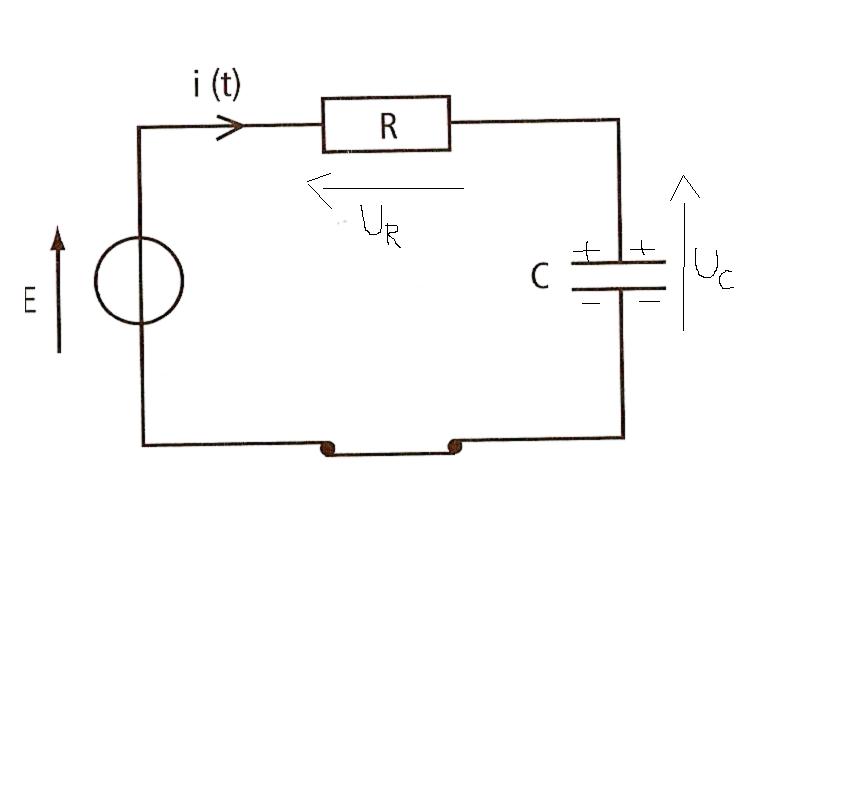
1) Refaire un schéma du montage et noter sur celui-ci la charge du condensateur q(t) et les flèches-tension aux bornes de la résistance et du condensateur en convention récepteur. (voir schéma plus bas).
2) Établir l'équation différentielle qui permet de déterminer la charge q(t) du condensateur.
3)La solution de cette équation différentielle s'écrit : q(t) = A+Ke-t/RC
a) Lorsque t tend vers l'infini, la charge q(t) est constante ; exprimer cette charge en fonction de E et C.
b) Exprimer la charge q(t) solution de l'équation différentielle sachant qu'à t=0, on ferme l'interrupteur, le condensateur étant déchargé.
c) En déduire l'expression de l'intensité du courant dans le circuit.
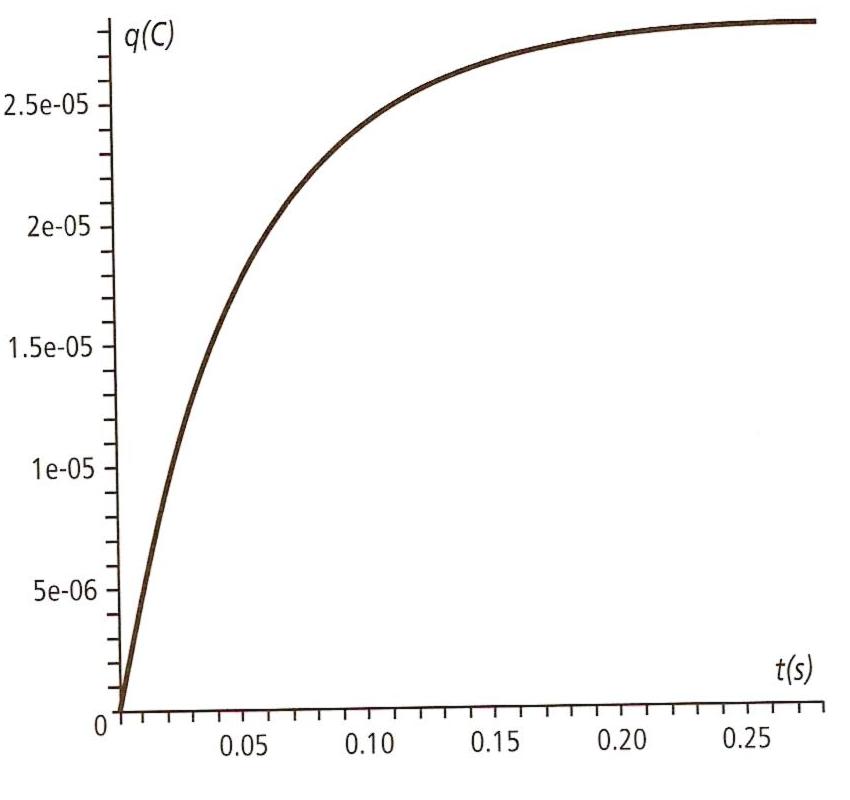
4) l'enregistrement de l'évolution de la charge q en fonction du temps est présenté par le graphique suivant (voir plus bas). On donne R=11 K ; E=6,0 V ; C=4,7
; E=6,0 V ; C=4,7  F.
F.
a) Exprimer et calculer la constante de temps du circuit.
b) Vérifier graphiquement cette valeur en utilisant la méthode de la tangente.
5) On double la valeur de la tension aux bornes du générateur. Représenter l'allure de q(t).
a) La constante de temps du circuit sera t'elle modifiée ?
b) la valeur de la charge en régime permanent sera t'elle modifiée ?
1) voir le 1er schéma, est ce correcte ?
2) je n'arrive pas
Bonjour,
1. OK 
2. Utilise les lois des circuits : loi des mailles, loi d'Ohm, relation caractéristique du condensateur...
Oui, c'est correct mais tu ne réponds pas à la question. On te demande une équations différentielle vérifiée par q(t) et non pas Uc(t). Quel lien existe-t-il entre q(t) et Uc(t) ?
2)
E - Ri - Uc = 0
et dq/dt = i
et q = C.Uc
E - Ri - Uc = 0
E - R.dq/dt - q/C = 0
R.dq/dt + q/C = E
dq/dt + q/(RC) = E/R
-----
Sauf distraction. 
bonsoir, je voudrais reprendre l'exo où je m'étais arrêté.
pour la question 2, n'y aurait il pas une écriture plus simple à trouver ?
Bonsoir,
2. Tu souhaiterais simplifier ?! Il n'y a pas plus simple non... C'est l'équation différentielle vérifiée par
lors de la charge.
À la limite, tu peux (si tu le souhaites) introduire la constante de temps du circuit , ce qui donne :
.
Au passage, tu as compris maintenant comme on fait pour établir cette équation différentielle ?
Je vais numéroter les différentes équations et puis tu me diras ce que tu ne comprends pas.
(1) D'après la loi des mailles, on a : soit
.
(2) Or, d'après la loi d'Ohm, on a donc, en reportant dans la dernière équation du (1), il vient :
.
(3) Or, d'après la relation caractéristique du condensateur, on a soit
donc, en reportant dans la dernière équation du (2), il vient :
.
(4) Or, d'après la définition de l'intensité du courant, on a 3$ i(t)=\frac{dq(t)}{dt} donc, en reportant dans la dernière équation du (3), il vient : soit, en divisant par
tous les membres,
.
Il n'y a pas "plus simple" que d'application les lois des circuits : loi des mailles, loi des nœuds (inutile ici), loi d'Ohm, relation caractéristique du condensateur, relation caractéristique de la bobine (inutile ici)...
E c'est la force électromotrice du générateur (f.é.m.). En fait, tu charges ton condensateur avec un générateur qui délivre E = 15 V par exemple. Ici, on ne te dit pas combien il vaut, on te dit simplement que c'est E. Pareil pour la résistance R du conducteur ohmique et pour la capacité C du condensateur : tu n'as pas de valeurs numériques, tu les utilises avec les lettres qui les représentent.
Non, pas encore. Utilises l'équation différentielle : on te dit que quand t tend vers plus l'infini, q(t) est constante. Donc dq(t)/dt=0 donc, d'après l'équation différentielle, à quoi est égal q(t) ?
Il n'y a plus de dq(t)/dt : c'est la dérivée de la fonction q. Or on te dit que lorsque t tend vers plus l'infini, q(t) est constante. Or la dérivée d'une fonction constante est nulle, donc dq(t)/dt tend vers 0 lorsque t tend vers plus l'infini.
L'équation différentielle te fournit donc (lorsque t tend vers plus l'infini) q(t)/(RC)=E/R d'où q(t)=CE. C'est bon ?
Non, il faut exprimer q(t) pour tout t. Sauf que tu as encore une inconnue qui est K dans l'expression de q(t) et la condition initiale va te permettre de la déterminer.
On te dit q(t)=A+Kexp(-t/(RC)). A et K sont inconnues pour le moment. Mais tu viens de voir quand quand t tend vers plus l'infini, q(t) tend vers CE. Or d'après son expression, q(t) tend vers A lorsque t tend vers plus l'infini (car exp(-t/(RC)) tend vers 0 lorsque t tend vers plus l'infini) : donc A=CE. Tu as donc q(t)=CE+Kexp(-t/(RC)) : il n'y a donc plus que K qui est inconnu.
On te dit qu'à t=0, le condensateur est déchargé : on a donc q(t=0)=0. Or d'après son expression, q(t=0)=CE+K. Donc CE+K=0 d'où K=-CE.
Finalement, . C'est bon ?
À force de faire des exercices sur ce chapitre, tu vas y arriver petit à petit : ce sont souvent les mêmes raisonnements à transposer dans tel ou tel exercice.
Si tu avais réinjecter la solution proposée dans l'équation différentielle (comme tu le proposais), tu serais également arriver au résultat mais tu aurais mis plus de temps et tu aurais répondu à plusieurs questions à la fois.
Je t'ai juste montré qu'il y avait plus court pour répondre uniquement à la question posée.
Ce que j'ai fait avec q(t=0)=0, tu devrais savoir le faire normalement : il s'agit d'exploiter la condition initiale pour déterminer la constante (ça a dû être fait plusieurs fois dans le cours d'électricité : dipôle RC, RL, LC).
Oui  (personnellement, je laisserai RC plutôt que
(personnellement, je laisserai RC plutôt que parce qu'on te parle de
plus tard dans l'énoncé, mais fondamentalement ce n'est pas faux)
je suis au cned, ce n'est vraiment pas facile
J'imagine, en effet...
Comment ça se passe ? Tous tes cours sont pas écrit ? Tu ne vois jamais de professeur ? Si c'est le cas, c'est normal que tu rencontres des difficultés : il est difficile de comprendre un cours sans qu'il ne soit expliqué par un professeur...
J'imagine, en effet...
Comment ça se passe ? Tous tes cours sont pas écrit ? Tu ne vois jamais de professeur ? Si c'est le cas, c'est normal que tu rencontres des difficultés : il est difficile de comprendre un cours sans qu'il ne soit expliqué par un professeur...
tous les cours sont dans des livres et libre à nous de s'organiser. je ne vois jamais de professeur
Tu as sorti ça de ton cours ? Auquel cas ce n'est pas ce qu'il fallait faire...
On vient de montrer que .
Or, d'après la définition de l'intensité du courant, . Donc
est la dérivée de
.
donc
. Le premier terme est constant donc sa dérivée est nulle, le deuxième est de la forme
et se dérive donc en
. Tu as compris comment on dérivait cette fonction ?
D'où, comme annoncé, .
C'est bien ça.
Et si jamais on te demande de montrer que est bien homogène a un temps, tu peux dire :
(*) apparaît dans la loi d'Ohm :
donc
donc
est homogène à :
;
(*) apparaît dans la relation caractéristique du condensateur :
donc
donc
est homogène à :
.
Et comme ,
est homogène à :
.
est donc bien homogène à un temps et s'exprime alors en secondes.
Mais ce n'était pas demandé  (petit complément au cas où)
(petit complément au cas où)
toujours bon à savoir.  =51,7.10-3 s soit 0,052 s.
=51,7.10-3 s soit 0,052 s.
j'ai tracé la tangente sur le graphique, les 2 résultats sont cohérents
5)a) pourrais tu me dire comment se comporte le condensateur si on modifie la tension ou l'intensité et donc dans ces 2 cas, comment varie  et quels sont les aspects des courbes représentant la tension en fonction de t, l'intensité en fonction de t. (lors de la charge)?
et quels sont les aspects des courbes représentant la tension en fonction de t, l'intensité en fonction de t. (lors de la charge)?
j'espère que tu m'a compris, en fait je te demande une petite explication de cours sur les facteurs qui peuvent modifier la charge d'un condensateur. merci
Bonjour,
donc sa valeur ne dépend que de la résistance du conducteur ohmique et de la capacité du condensateur. La constante de temps du circuit n'est donc pas modifiée si on double la valeur de la tension aux bornes du générateur (réponse à la question 5a). On chargeait le condensateur sous une tension
et maintenant on le charge sous une tension
(mais
ne dépend pas de
).
En régime permanent (c'est-à-dire quand t tend vers plus l'infini), on a vu à la question 3a que . Or on a doublé la tension du générateur, donc
(réponse à la question 5b).
Ainsi, si tu traces la courbe de : elle tend vers
mais
reste le même.
La première courbe était une exponentielle croissante qui tendait vers CE.
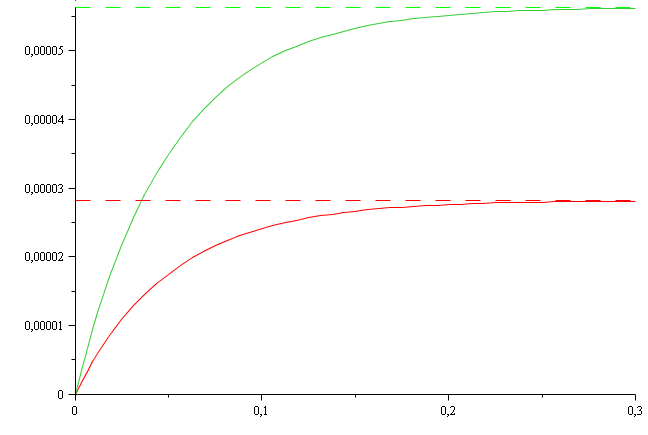
Celle-ci est une exponentielle croissante qui tend vers 2CE (puisqu'on double la tension délivrée par le générateur). Par contre, la constante de temps reste inchangée : la courbe ne tend donc pas plus ou moins vite que l'ancienne mais bien à la même vitesse (ou dis différemment : la tangente à l'origine doit couper son asymptote à un point de même abscisse, qui est la constante de temps, que pour la première courbe).
En rouge : charge du condensateur sous la tension E. Elle tend vers CE.
En vert : charge du condensateur sous la tension 2E. Elle tend vers 2CE.
Mais si tu calcules la constante de temps sur les deux courbes, tu vas trouver la même valeur puisque la constante de temps vaut RC : elle ne dépend pas de E (la tension délivrée par le générateur).
Au final, seul l'asymptote horizontale est modifiée : pour l'une c'est q(t)=CE et pour l'autre c'est q(t)=2CE.
ok mais y'a t'il moyen de tracer ces courbes sur la calculette ou sur une feuille? je ne comprend pas trop comment on trace la 2ème courbe
Oui, bien sûr, tu peux les tracer à la calculatrice.
La première courbe (la rouge) représente la fonction .
La seconde courbe (la verte) représente la fonction .
Pour la première (et ce sera le même principe pour la seconde), tu tapes C*E*(1-exp(-X/(R*C))) en remplaçant C, E et R par leurs valeurs numériques (données dans l'énoncé).
Si tu veux justes tracer l'allure, tu vois que q(0)=0 et que q(t) tend vers CE quand t tend vers plus l'infini. Donc la droite d'équation q(t)=CE est asymptote horizontale à la courbe. Tu traces donc une exponentielle qui part de 0 et qui tend vers CE.
Idem pour la seconde courbe, sauf qu'elle tend vers 2CE (mais elle monte à la même vitesse : le calcul de la constante de temps à l'aide de la tangente à l'origine doit donner le même résultat pour les deux courbes).
Une application numérique sans unité n'a aucune valeur ! Et attention aux nombre de chiffres significatifs. Mis à part ces deux points, c'est correct 
oui pardon, c'est en coulomb. ici, il doit y avoir un seul chiffre après la virgule ?
mais pour refaire l'allure de la courbe q(t)=2CE je dois refaire un schéma avec les 2 courbes? car je n'ai pas de place sur le graphe donné dans l'énnoncé ?
C'est bien en coulomb. Toutes les données de l'énoncé possèdent deux chiffres significatifs donc tes résultats doivent être donnés avec deux chiffres significatifs (et non pas trois comme tu l'avait écrit).
J'ai l'impression qu'on ne te demande que l'allure de q(t) lorsqu'on double la tension (donc ma courbe verte). Mais je pense qu'il serait pas mal de représenter les deux ensemble pour voir que la seule différence est la valeur limite (CE pour l'une et 2CE pour l'autre).



