Inscription / Connexion Nouveau Sujet
Champ g
Bonjour j'aimerais de l'aide. Merci
Dans la savane, un colon chasseur et son guide autochtone se perdent de vue en pleine nuit.
Pour retrouver son guide, le colon se sert d'un pistolet qui lance des fusées éclairantes. Sur la notice des fusées éclairantes, on trouve les informations suivantes ;
Cartouche qui lance une fusée éclairante s'allumant 1,0 seconde après son départ du pistolet et éclaire d'une façon intense pendant 6 secondes environ.
Masse de la fusée éclairante :
= 58g
On se place dans le référentiel terrestre supposé galiléen.
Le champ de pesanteur est considéré comme uniforme, de valeur g=9;8m/s².
On négligera toutes les actions dues à l'air ainsi que la perte de masse de la fusée pendant qu'elle brille et on considère cette dernière comme un objet ponctuel .
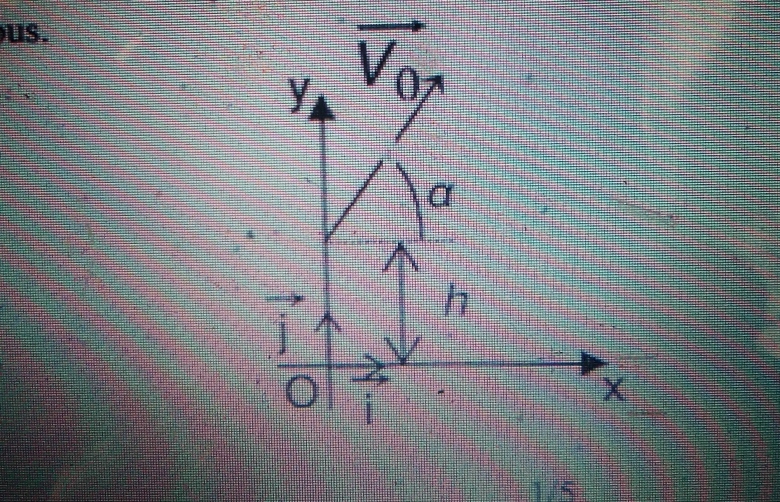
On définit un repère ( O ;
;
) avec O au niveau du sol et tel que la position initiale de la fusée éclairante à la sortie du pistolet soit à une hauteur h=1;8m. Le vecteur vitesse initiale
est dans le plan (O ; x ; y ) ; Ox est horizontal et Oy est vertical et orienté vers le haut .
A l'instant t=0 s, le vecteur vitesse de la fusée éclairante fait un angle
 =53° avec l'axe Ox et sa valeur est
=53° avec l'axe Ox et sa valeur est = 50m/s. On pourra se référer au schéma ci-dessous.
1-
1-1- Donner les coordonnées à l'instant t=0s des vecteurs positions et vitesse
du système .
1-2- Énoncer le théorème du centre d'inertie et l'appliquer pour déterminer les coordonnées du vecteur accélération de la fusée éclairante
1-3- Déterminer les équations horaires du mouvement de la fusée éclairante.
1-4- En déduire l'équation cartésienne de la trajectoire de la fusée éclairante.
1-5- Donner la nature de sa trajectoire et déterminer la valeur de sa vitesse au sommet de sa trajectoire.
Je bloque sur la 1-5/ merci de m'éclairer.
Bonjour pfff,
Questions 1 à 4 : tu as réussi à la faire, malgré tout, je te joins une fiche de cours sur le sujet : ![]() Mouvement d'un projectile dans le champ de pesanteur
Mouvement d'un projectile dans le champ de pesanteur
A noter qu'il y a effectivement une hauteur H initiale à considérer dans l'étude y(0) = h.
Question 5 : si tu as déterminé l'équation de sa trajectoire, tu as dû constater qu'on obtient une équation de la forme y(x) = a.x² + b.x + c
C'est :
- une droite ?
- une hyperbole ?
- une parabole ?
- une courbe quelconque ?
Ensuite, que peut-on dire de la vitesse lorsque la fusée atteint le sommet de la trajectoire ?

D'abord vraiment merci gbm de m'avoir répondu je perdais presque espoir vu que mon sujet est tellement long.
La nature j'ai trouvé une parabole.
Et ensuite au sommet de la trajectoire j'ai dit la vitesse est nulle donc VS=0m/s
C'est cela ?
Il faut toujours faire preuve de patience : il fait globalement beau en France, on sort de 2 mois de confinement, tout le monde en profite pour mettre le nez dehors (tout en respectant les gestes barrière, cela va sans dire)  !
!
Oui c'est ça : une parabole !
Ensuite, attention au raisonnement : si le vecteur vitesse était nul, alors ton mouvement ne serait plus régit par une parabole ; tu en viendrais à étudier un mouvement de chute libre verticale.
En fait, une composante du vecteur vitesse est nulle : laquelle ?
Aide-toi de la fiche si nécessaire

Il faut toujours faire preuve de patience
Ça c'est vrai. Désolé
En fait, une composante du vecteur vitesse est nulle : laquelle ?
Je vois
C'est Vsy c'est à dire la composante verticale qui est nulle
Donc je dois calculer avec Vsx ? Mais comment
Oui TB !
Si Vsy = 0 tu peux déterminer la durée pour laquelle on obtient cette condition avec son équation horaire.
Puis tu injectes cette relation trouvée pour le temps dans Vsx 
Je t'en prie  !
!
A une prochaine fois !
PS : pour l'autre sujet, je laisse odbugt1 revenir, on est samedi en fin d'après-midi, il n'y a pas d'urgence
j'aimerais encore des indices pour la suite. Merci
2-Entre quelles distances limites doit être situé le guide par rapport au colon, pour être éclairé par la fusée ? Justifier la réponse
3-Déterminer la valeur de la durée du vol de la fusée éclairante
Au temps pour moi, je pensais que c'était terminé !
Si je comprends bien l'énoncé, il faut que tu détermines la portée de ta parabole, c'est expliqué dans la fiche

1-5- Donner la nature de sa trajectoire et déterminer la valeur de sa vitesse
J'ai trouvé la durée mais je ne peux pas l'injecter dans Vsx puisqu'il n'y a pas le temps la bas
Au temps pour moi, je suis allé trop vite en besogne ; le mieux pour les fois suivantes serait de détailler tes réflexions dès le début 
On a la composante Vsy = 0
Sauf erreur de ma part, tu as dû trouvé
La réponse était donc immédiate, connaissant la vitesse initiale et l'angle de départ

Je suis vraiment désolé odbugt1 m'a fait la remarque.
La prochaine fois je recopie tout mon sujet et je mettrai les détails.
Effectivement !
2-Entre quelles distances limites doit être situé le guide par rapport au colon, pour être éclairé par la fusée ? Justifier la réponse
Concernant la parabole voici mon équation : Y = -5,95.10^-3X² + 1,4X + 1,8
A la distance limite YL =0 on obtiens donc une équation du second degré. Au final je trouve XL = 236m
Cette valeur me met un peu dans le doute et je ne sais pas comment justifier
Bonjour pfff,
La prochaine fois je recopie tout mon sujet et je mettrai les détails.
Super !
Effectivement !
C'était donc beaucoup plus simple que ma proposition initiale
Concernant la parabole voici mon équation : Y = -5,95.10^-3X² + 1,4X + 1,8
N'ayant pas le détail, je te fais confiance pour cette équation cartésienne de la trajectoire.
Concernant ton calcul de la portée (YL = 0), si XL = 236 m
alors Y = -5,95.10-3 * (236)² + 1,4 * 236 + 1,8 = 0,80 m => je pense que cela est dû aux erreurs d'arrondi, donc cette valeur me semble correct.
Je pense que l'énoncé suppose que le guide est parti devant le chasseur et qu'il ne doit pas être au-delà de la portée de la fusée pour pouvoir évaluer d'où elle vient

Merci, pour terminer :
3- Déterminer la valeur de la durée du vol de la fusée éclairante.
Au sommet de la trajectoire Ys = 0  -g ts + Vo sin
-g ts + Vo sin = 0
= 0
 ts = 4,18 s
ts = 4,18 s
4-Le guide arrêté à d=25m du colon, démarre juste une seconde après le tir de la fusée, avec un mouvement rectiligne d'accélération a' = 14,8m/s² en cherchant à aller dans la zone éclairée.
4-1- Donner l'équation horaire du mouvement du guide en gardant les mêmes origines de dates et d'espace que pour la fusée éclairante.
x = a't² + Vot + xo
 x = 7,4t² + 25
x = 7,4t² + 25
4-2- La fusée pourrait t'elle directement éclairer la tete du guide lors de son mouvement ? Justifier la réponse .
la distance limite pour être éclairé par la fusée est à 236m le guide etant situé à 25m sera éclairé
4-3-Si oui, déduire la position du guide par rapport au colon à cet instant précis
Besoin d'aide
Oui, c'est vrai
On a l'équation horaire du mouvement du guide et la durée de vol de la fusée.......
Merci et bonne journée 
Bonsoir gbm,
Je reviens sur cet exercice car il ya une question que je trouve qu'on a pas totalement achevée. La voici :
2-Entre quelles distances limites doit être situé le guide par rapport au colon, pour être éclairé par la fusée ? Justifier la réponse
regarder à partir du 23-05-20 à 21:33
Voila la question dit :
2-Entre quelles distances limites doit être situé le guide par rapport au colon, pour être éclairé par la fusée ? Justifier la réponse
le '' Entre '' me dit que on doit trouver une valeur comprise entre un intervalle
Oui mais raisonne physique : tu as le chasseur qui tire la fusée lumineuse à un instant t = 0 s => la fusée décolle ; sa trajectoire est une parabole et celle-ci finit par tomber au sol au bout d'un certain temps. Le guide ne peut la voir que s'il se trouve sous la parabole parcourue par la fusée : conclusion ?
Fais un schéma si nécessaire.

Mais c'est un peu bizarre on ne connait pas le sens dans lequel il lance la fusée.
Si le colon lance à droite et que le guide est à gauche ou devant, c'est impossible qu'il soit éclairé.
C'est tout ça qui me perturbe au niveau de cette question.
On ne sait pas si le guide est devant ou derrière le colon.
2-Entre quelles distances limites doit être situé le guide par rapport au colon, pour être éclairé par la fusée ? Justifier la réponse
Donc je peux dire que le guide doit être situé à au plus 236m par rapport au colon pour être éclairé par la fusée ( On avait déjà calculé la portée )
Justification : la trajectoire de la fusée étant une parabole le guide ne peut la voir s'il se trouve entre la position du colon et la portée de la fusée
C'est correct ?


