Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Champ electrostatique total

Posté par
Oussamamlm 20-12-17 à 23:40

Bonsoir
j'ai une question dans un exercice que j'ai pas pu la résoudre voilà l'énoncé :
Soit 3 charges ponctuels identiques . chaque charge est situé sur le sommet d'un triangle équilatéral de coté (a) .trouver l'intensité de champ total en un point M distant de centre O du triangle de x (OM=x) et appartenant à la droite passant par O et perpenduculaire au plan du triangle en fonction de (k,q,a,x)
je sais que E = k . lql.lql/r² quelqu'un peut m'aider ? et merci d'avance

Posté par
odbugt1re : Champ electrostatique total 21-12-17 à 11:31

Bonjour,

Citation :
je sais que E = k . lql.lql/r²
A revoir.
Il semble que tu confondes le champ créé en un point avec une force qui n'existera que si on place une charge en ce point.


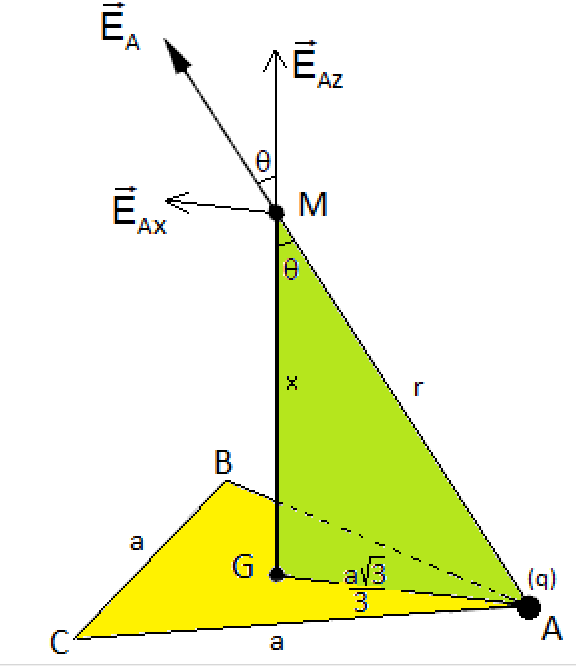
Le schéma joint devrait t'aider.

Il représente le champ \vec {E_A}créé au point M par une des trois charges (supposées positives pour la clarté de la figure) placées en A,B,C
Il représente aussi la composante verticale \vec {E_Az} de ce champ
La composante horizontale n'est pas représentée, car, vu la symétrie de la répartition des champs cette composante disparait au cours du calcul.
Il reste à manipuler des règles simples de géométrie pour obtenir l'expression de EAz et ensuite celle du champ total créé en M

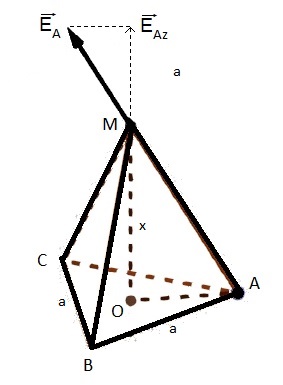
Champ electrostatique total

Posté par
Oussamamlmre : Champ electrostatique total 24-12-17 à 20:29

oui j'ai pas fais attention pour la relation bref
E= k . q/r² j'ai demandé un camarade et il m'a dit qui l'a pu arriver à r = 3OM mais on demande dans l'exercice 3 champs donc pas une seule représentation n'est ce pas ? et ça va donner un triangle équilateral aussi symetrique a celui d'en bas  

Posté par
odbugt1re : Champ electrostatique total 24-12-17 à 21:53


\\ \large \\ \textrm {Je pose} \\ AM=r \\ cos( \theta )= \left(\overrightarrow{E_{Az}},\overrightarrow{E_{A}}\right) \\ \\ \textrm {Module du champ créé en M par la charge placée en A} \\ E_A= \dfrac{k | q | }{r^2} \\ \textrm {Calcul de} \;E_Az \\ E_{Az}= \dfrac{k | q | }{r^2}cos( \theta ) \\ \textrm {Géométrie dans les triangles ABC et AOM} \\ cos( \theta )= \dfrac{x}{r} \\ \\ OA=a \frac{ \sqrt{3} }{3} \\ \\ r^2=x^2+ \frac{a^2}{3} \\ \textrm {Module de } E_{Az} \\ \large E_{Az}=\dfrac{k| q |x }{\left(x^2+ \dfrac{a^2}{3}\right)^{\frac{3}{2}}} \\ \textrm {Les charges placées en B et C ont le même effet au point M que celle placée en A. } \\ \textrm {Pour des raisons de symétrie les composantes horizontales des trois champs s'annulent } \\ \textrm {Les composantes verticales s'additionnent } \\ E_E_{Total}=3E_{Az} \\ \\ \large E_{Total}=\dfrac{3k| q |x }{\left(x^2+ \dfrac{a^2}{3}\right)^{\frac{3}{2}}} \\

Posté par
Oussamamlmre : Champ electrostatique total 24-12-17 à 22:02

J'ai pas compris Eaz vous pouvez l'expliquez s'il vous plait

Posté par
Oussamamlmre : Champ electrostatique total 24-12-17 à 22:36

J'ai compris la Eaz mais j'ai pas compris la puissance 3/2 sur le denumerateur

Posté par
odbugt1re : Champ electrostatique total 25-12-17 à 10:32


Voir figure ci-dessous
\large E_{Az}=E_A\cdot cos(\theta)=E_A \cdot\dfrac{x}{r} =k\cdot\dfrac{ |q| }{r^2} \cdot\dfrac{x}{r}= \dfrac{k|q| x}{r^3}

Triangle rectangle AGM

r= \sqrt{x^2+ \dfrac{a^2}{3} }= \left(x^2+ \dfrac{a^2}{3}\right) ^ \frac{1}{2}

r^3= \left(x^2+ \dfrac{a^2}{3}\right) ^ \frac{3}{2}

Donc

E_{Az}= \dfrac{k| q| x}{\left(x^2+ \dfrac{a^2}{3}\right) ^ \frac{3}{2} }

E_{Total}=3E_{Az}= \dfrac{3k|q| x}{\left(x^2+ \dfrac{a^2}{3}\right) ^ \frac{3}{2}}

Champ electrostatique total

Posté par
Oussamamlmre : Champ electrostatique total 25-12-17 à 13:27

Merci beaucoup pour votre aide
j'ai demandé mon prof a propos de ça et le cos\theta de l'angle  GMA n'est pas celui de Eaz et Ea n'est pas la même est ce que c'est logique ?  

Posté par
odbugt1re : Champ electrostatique total 25-12-17 à 13:54

Si j'ai bien compris l'énoncé de ton exercice les deux angles dont tu parles sont opposés par le sommet donc égaux.
Sinon, merci de publier, quand tu l'auras, le corrigé donné par ton professeur.

Remarque : Sur mon dernier schéma j'ai noté par " G " le point " O " de l'énoncé ( centre du triangle ABC

Posté par
Oussamamlmre : Champ electrostatique total 25-12-17 à 19:13

oui c'est que j'ai compris aussi je sais pas pourquoi peut etre il n'a pas bien imaginé la figure

Posté par
odbugt1re : Champ electrostatique total 25-12-17 à 22:39

Reproduire la figure sur une feuille de papier est il si compliqué que tu ne puisses le faire ?


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !