Inscription / Connexion Nouveau Sujet
champ électrique ( énigme ) !
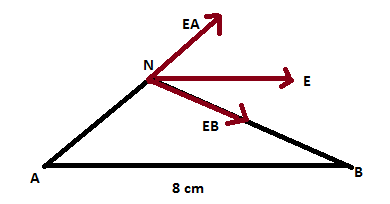
Soient deux charges ponctuelles q1= 1nC et q2= -8nC placées resp en deux pts A et B distants de d=8 cm .
en un point N le vecteur champ résultant par l'ensemble de deux charges a une direction parallèle à (AB) et une valeur E=2.67 * 104
déterminer AN
Salut,
Le champ de force est 9*10^9*Q/R²
on a en N
un champ de 9*10^9*q1/Ra² issu de A avec Ra la distance AN et a l'angle NAB
et
un champ 9*10^9*q2/Rb² issu de B avec Rb la distance BN et b l'angle NBA
Les composantes verticales s'annule donc
9*10^9*Iq1I/Ra² * sin a - 9*10^9*Iq2I/Rb² * sin b =0
donc q1/Ra² * sin a + q2/Rb² * sin b =0
donc q1/Ra² * sin a = -q2/Rb² * sin b
De plus Ra sin a = Rb sin b
donc q1/Ra² * sin a = -q2/Rb^3 *Rb* sin b = -q2/Rb^3 *Ra* sin a
donc -q1/Ra^3 = q2/Rb^3
De plus on sait que les composantes verticales s'ajoutent pour donner 2.67 * 10^4 donc
9*10^9*q1/Ra² * cos a - 9*10^9*q2/Rb² * cos b = 2.67 * 10^4
donc
q1/Ra² * cos a - q2/Rb² * cos b = 2.97 * 10^-6
donc
q1/Ra² * cos a - q2/Rb^3 *Rb* cos b = 2.97 * 10^-6
Or Ra cos a + Rb cos b = 0.08
donc Rb cos b = 0.08 - Ra cos a
donc
q1/Ra² * cos a - q2/Rb^3 *(0.08 - Ra cos a) = 2.97 * 10^-6
donc
q1/Ra² * cos a + q1/Ra^3 *(0.08 - Ra cos a) = 2.97 * 10^-6
donc
0.08 q1/Ra^3 = 2.97 * 10^-6
Donc Ra^3 = 2.97*10^-6/0.08
Donc Ra = (2.97*10^-6/0.08)^(1/3) = 0.033 m
j'espère ne pas m'être emmêlé les pinceaux