Inscription / Connexion Nouveau Sujet
Champ de gravitation
Bonjour, j'ai un exos de phisique à effectuer pour demain, dont les questions sont les suivantes :
1 a) exprimer la force exercée par la terre sur la lune F(T/L) en fonction de ML, MT et D( TL)
b) exprimer également cette force en fonction du champ de gravitation de la Terre
G(T) et de la masse de la Lune M(L)
c) en déduire l'expression du champ de gravitation G(T)
d) indiquer alors ses caractéristiques
2) faire de même pour le champ de gravitation G(S) dû au Soleil
3) reproduire le schéma. le compléter en représentant à l'échelle les deux champs G(S) et G(T) au niveau de la Lune.
4) déterminer les caractéristiques du champ résultant G= G(S) + G(T).
PS: Tout les G sont des vecteurs
Pour la question 1 a), j'ai fait F(T/L) = G (M(L)*M(T))/D(TL)² vecteur U (LT)
Mais je ne comprends pas pour la 1 b)
Merci de votre aide 
Bonsoir,
Déjà on écrit "physique" et non "phisique".
Ensuite, ce type d'exercice a déjà été posté, as-tu utilisé le moteur de recherche ?

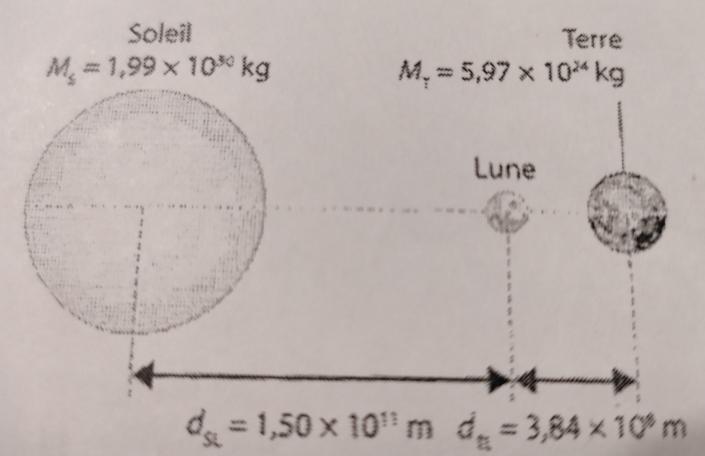
1 a) exprimer la force exercée par la terre sur la lune F(T/L) en fonction de ML, MT et D( TL)
En valeur, effectivement : F(T/L) = G*ML*MT/D(TL)²
b) exprimer également cette force en fonction du champ de gravitation de la Terre
G(T) et de la masse de la Lune M(L)
Par analogie au poids d'un solide de masse M(L), soumis au champ de gravitation terrestre G(T) :
P = F(T/L) = M(L)*G(T)
c) en déduire l'expression du champ de gravitation G(T)
F(T/L) = G*ML*MT/D(TL)² = ML*[G*MT/D(TL)²] = M(L)*G(T)
donc G(T) = G*MT/D(TL)²
d) indiquer alors ses caractéristiques
Je te laisse y réfléchir
2) faire de même pour le champ de gravitation G(S) dû au Soleil
Adapter le raisonnement fait précédemment pour cette question
3) reproduire le schéma. le compléter en représentant à l'échelle les deux champs G(S) et G(T) au niveau de la Lune.
A faire
4) déterminer les caractéristiques du champ résultant G= G(S) + G(T).
A faire
PS: Tout les G sont des vecteurs

Je ne comprends pas votre resonnement pour la question 1 b), " P = F(T/L) = M(L)*G(T)"
Et pour la question 1 c), "ML*{G*MT/D(T/L)²}= ML*GT"
Attention à ton orthographe : raisonnement.
On te demande de déterminer un champ de gravitation g.
Tu as vu dans ton cours de troisième que le poids P d'un solide de masse m soumis à un champ de gravitation g est P = m.g
Par analogie avec la force d'attraction gravitationnelle : F = G.m.M/d² = m*[G.M/d²]
alors si P = F on peut écrire que g = G.M/d²
c'est ce que j'ai fait avec les notations de ton énoncé.
Ok, merci pour vos explications 
Et, étant donner qu'il nous demande "d'exprimer", est ce que je doit le faire avec les valeurs ou littéralement ?
En général, exprimer c'est plus faire un calcul littéral.
Calculer c'est faire l'application numérique, mais pour moi tu vas avoir besoin des valeurs numériques pour déterminer le vecteur résultant.

Pour la question 1 d), ses caractéristiques sont les suivantes :
- le champ gravitationnel s'identifie au champ de pesanteur
-si le champ G s'applique sur une masse, il en résulte une force
C'est ça ?
Si tu te souviens de ton cours, une force peut être définie à partir de différents éléments qui permettent de caractériser un vecteur :
Sa direction
Son sens
Sa valeur ou norme calculé en newton et qui peut parfois être appelée intensité
Son point d'application

Le vecteur champ de gravitation est un vecteur comme un autre, il suffit d'être vigilant dans l'analogie faite dans cet exercice.
Un schéma peut aider

Non, simplifie toi la vie en représentant le vecteur à la distance D(TL) puisque c'est la valeur du champ à cette distance 
La direction, c'est Terre- Lune
Le sens, c'est de la Lune à la Terre
Sa norme, (il fait que je la calcule)
Son point d'application, ?
Mais pour la question 1, si je doit calculer F(T/L),
Je ne peux pas, car on ne me donne pas la valeur de ML
Je pense qu'il faut juste exprimer littéralement pour la première partie, mais avec les valeurs pour la suite avec le soleil pour ensuite faire le schéma
Et pour la question 2, je refais tout le développement où je marque directement que
G(s)= G*{M(s)/D(S/T) étant donner que
G(T)= G*{M(T)/D(T/L)
Seules les valeurs de G(T) et G(S) sont utiles pour déterminer les caractéristiques du champ résultant, donc M(L) n'est pas nécessaire.
Un résultat sans détail ni unité c'est 0 le jour d'un examen.
Concernant enfin ton développement, il manque un ² à la distance, en vertu du rappel du cours refait dans mon message du 17-11-19 à 18:26
Étant donné que G(T) et G(S) sont des vecteurs, je doit mettre juste U en vecteur unitaire ou U(TL) par exemple ?
Et pour G(S), je le calcul avec la distance Soleil-Terre ?
Si tu as compris le raisonnement des messages du 17-11-19 à 17:35 et 17-11-19 à 18:26 tu devrais t'en sortir, il te suffit de t'en inspirer et de détailler tout comme je l'ai fait.
Étant donné que G(T) et G(S) sont des vecteurs, je doit mettre juste U en vecteur unitaire ou U(TL) par exemple ?
Oui, fais comme tu as l'habitude de procéder

Donc ses caractéristiques sont les suivantes :
-la direction c'est Soleil-Lune
-le sens c'est du Soleil à la Lune
-ça norme c'est 5,8E-3 N/kg
-son point d'application, c'est le centre d'inertie de la lune
Donc ses caractéristiques sont les suivantes :
-la direction c'est Soleil-Lune
-le sens c'est du Soleil à la Lune
-ça norme c'est 5,8E-3 N/kg
-son point d'application, c'est le centre d'inertie de la lune
Oui sauf pour le sens : c'est le Soleil qui attire la Lune ...
Comment peut on " reproduire à l'ÉCHELLE les deux champs G(S) et G(T)" ?
Tu définis une échelle : 1 cm <=> xxx N/kg que tu reproduis sur ton schéma, judicieusement choisie
Pour la question 4), il te suffit de faire une somme vectorielle qui correspond à ton cours de seconde vue en maths

C'est que tu n'as pas choisi une échelle adéquate ou alors que tes applications numériques ne sont pas correctes 
C'est bien ce que je pensais, tu n'as pas pris en compte ma remarque du 18-11-19 à 13:02 sur le carré de la distance ...
Alors pourquoi écrire ceci ?
Donc je peux faire :
3,84E8 --> 1 cm
1,5E11 --> ?
ça n'a aucun sens par rapport aux normes trouvées pour les vecteurs G(T) et G(S) ...
Aux normes des vecteurs et non des distances, c'est tout l'objet de l'exercice.
Je te rappelle que je n'ai qu'un scan de ton schéma, je ne sais pas quel taille réelle il fait pour choisir à ta place une échelle suffisamment grande pour être lisible, tout en tenant sur la feuille du schéma :
1 cm <=> xxx N/kg (xxx à choisir judicieusement)
donc 2,70.10-3 N/kg <=> ... cm
et
5,90.10-3 N/kg <=> ... cm
Il faut ensuite reporter les deux vecteurs sur le schéma, connaissant leurs caractéristiques :
- point d'application
- droite d'action
- sens
- valeur (à l'échelle)


 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site
