Bonsoir, j'avais un problème dans la résolution d'un exercice !
Données :
m=50.0 g
M= 50.0 g
R= 40 mm
a= 200 mm
g=9.81 m.s-2
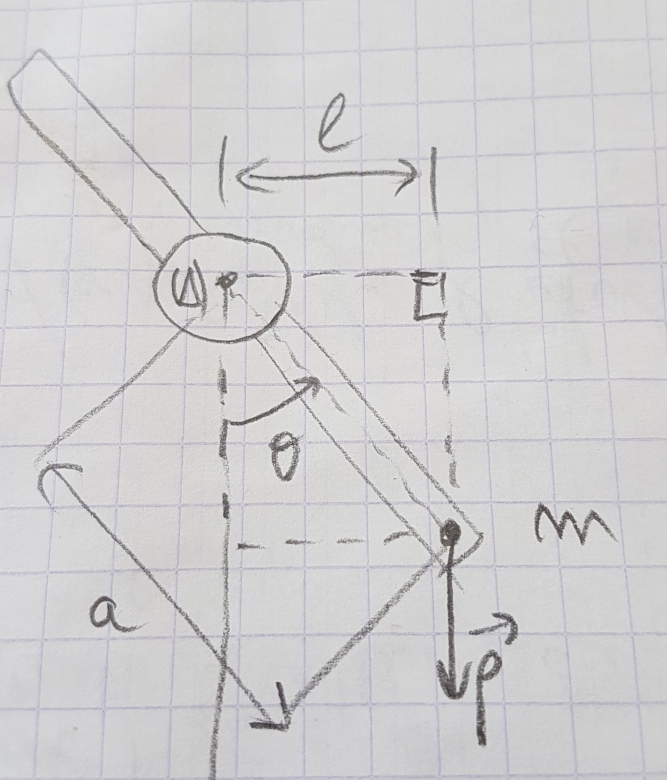
Pour cette étude, on réalise le montage de la figure 3.
Figure 3


Ce montage est constitué d'une poulie de rayon R sur la jante de laquelle on enroule un fil inextensible dont on néglige la masse. un bras diamétral, solidaire de la poulie, porte une paire de plots équidistants de l?axe.
L?ensemble poulie - bras diamétral est monté sur un roulement à billes et peut tourner autour d'un axe horizontal (?) avec le minimum de frottements. Son centre de masse est situé sur (?).

La masse M, suspendue à l?extrémité du fil, provoque la rotation du dispositif. Les plots sont destinés à recevoir une masselotte de masse m, que l'on considérera comme ponctuelle.

Rappel - Le moment d'inertie Jm, par rapport à un axe de rotation ? d'une masse ponctuelle m située à une distance d de l?axe ?, a pour expression Jm=ml

.
I. Première méthode
Pour déterminer le moment d'inertie J par rapport à l'axe (?) de l'ensemble poulie-bras diamétral, on réalise la manipulation suivante.
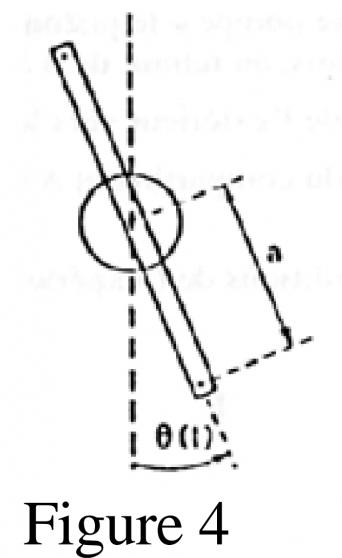
On adapte une masselotte sur l?un des plots, à la distance a de l'axe (?) (figure 4).

On écarte le bras d?un petit angle ?0 par rapport à la verticale et on abandonne le système sans vitesse initiale à la date t=0. On mesure la période T0 des petites oscillations (on fera l?approximation sin?0=?0, ?0 étant exprimé en radian.

À chaque instant t, l?écart angulaire entre le bras et la verticale est noté ?(t).
I.1. Etablir l?équation différentielle à laquelle satisfait ?(t).
I.2. En déduire l'expression de ?(t).
I.3. Exprimer la période T en fonction de J, m, a, et de l'accélération de la pesanteur g.
I.4. On mesure T=1.20 s. En déduire la valeur numérique de J.

je vous epargne ainsi la seconde partie.
j'ai un problème d'abord au niveau de la première question. je suid consciente qu'il faut utiliser le théorème de l'accélération angulaire, mais je n'arrive pas à trouver le moment du poids car il me faut avant tout le centre d'inertie.
je n'ai jamais eu à faire à ce genre de montage donc je ne sais pas trop comment opérer pour trouver le centre d'inertie
merci, en espérant trouver de l'aide.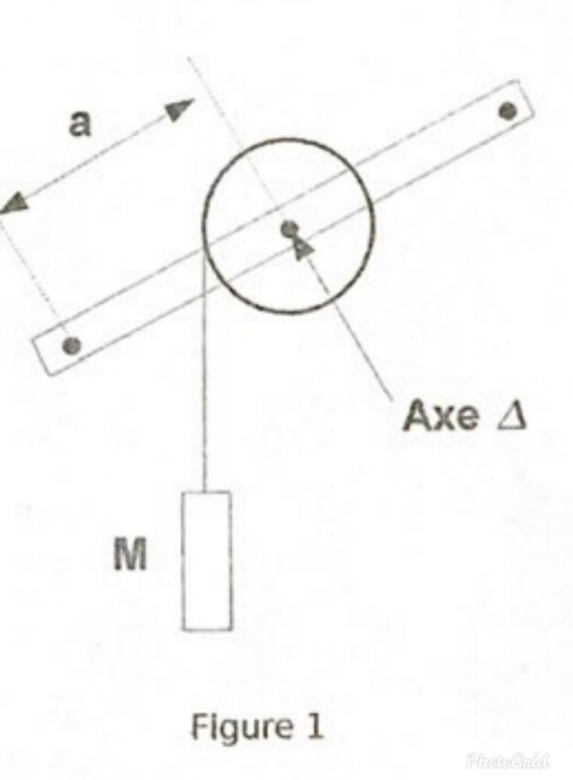



** doublon figure 1 supprimé **