Inscription / Connexion Nouveau Sujet
centre d inertie
Bonjour,
Lors de la journée de l'excellence en physique-chimie dans votre localité.
Il est demandé a chaque élevé candidat au prix de l'excellence , d'effectuer un choix entre trois billes billes de masses respectives m1,vm2 et m3 à faire glisser sur la piste représentée par la figure ci dessous :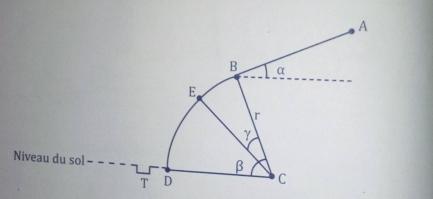
Cette piste est constitué d une partie AB rectiligne de longueur l=2 m, faisant un angle a=30° avec l'horizontal et d'un arc de cercle BD de rayon r=1 m
S
ur AB, il existe des forces de frottements équivalentes a une force unique F supposé constante de valeur F=0,2 N. Les forces de frottements sur la partie BD sont négligeable les billes sont supposée ponctuelles.
L'objectif assigné aux candidats est de lâcher au point A sans vitesse ,la bille judicieusement choisie ,afin que elle puisse quitter la piste au point E pour aller se loger dans le trou T au bas de la piste sur le sol :
m1=50g,
m2=56,2g,
m3=52,6 g
B=l'angle BCD =75° et y=l'angle ECB=45°
En tant que candidat ,propose la solution' en utilisant g=9,8 m/s^2 comme intensité de la pesanteur :
1/ précise
1/1. Le système étudié
1/2 le référentiel d étude de mouvement
2/ déterminer l expression de la vitesse de la bille
2/1 au point B en fonction de sa masse m,g.F l et a
2/2 au point E où elle quitte la piste ,en fonction de sa masse m,g,F,l,r,a ,B et y
3/ exprime la réaction RN de la piste sur la bille au point E
4/ déduis des questions précédentes la masse de la bille qui convient pour être logée dans le trou T
Question1
Les trois billes
Question1/2
C'est le référentiel terrestre
Question 2/1
Appliquons le théorème de l'énergie cinétique entre A et B :
ECB-ECA=mgh -f*AB
1/2 mVB^2=mgsina*l-f*l
VB^2=2l/m(m gsina-f)
VB=
(2gsina*l -2f*l/m)
Question 2/2
Au point E
Je suis bloqué
___________
***Topic aéré : cela augmente la lisibilité de ton sujet et augmente tes chances t?obtenir une réponse***
Bonsoir
Appliquons le théorème de l énergie entre B et E
1/2_mVE^2-1/2mVB^2=w(RN)+w(p)
1/2mVE^2-1/2 mVB^2=m*g*h
Or h=sont*r
1/2m(VE^2-VB^2)=mgsinar
VE^2=2grsina+VB^2
VE=√2grsiny+(2gsina*l)-2f*l/m
3/ exprime la réaction Rn de la piste
Puisque le travail de la réaction est nul sur ce piste.
Je ne sais pas quelque théorème utilisé
bonjour
Question1
Les trois billes
pas tout à fait, le système étudié est UNE SEULE bille de masse m (on ne lance pas les 3 billes à la fois!)
Question1/2
C'est le référentiel terrestre
oui
Question 2/1
Appliquons le théorème de l'énergie cinétique entre A et B :
ECB-ECA=mgh -f*AB
1/2 mVB^2=mgsina*l-f*l
VB^2=2l(m gsina-f)/m
VB=
(2gsina*l -2f*l/m)oui (enfin des parentheses bien placées
Question 2.2
Appliquons le théorème de l énergie entre B et E
1/2_mVE^2-1/2mVB^2=w(RN)+w(p)
1/2mVE^2-1/2 mVB^2=m*g*h
jusque là, ca va (en précisant que RN ne travaille pas car …… )
mais qu'appelles-tu h ?
la suite est illisible (et fausse) :
Or h=sont*r
1/2m(VE^2-VB^2)=mg (sin a) r NON (si j'ai bien décodé!!)
VE^2=2gr sin a+VB^2
VE=√2gr sin y+(2g sin a*l)-2f*l/m
il suffit de faire apparaitre les triangles rectangles BHC et EKC (cf dessin)
et c'est immediat puisqu'on connait l'hypothénuse r et les angles 
et 
(non representés)
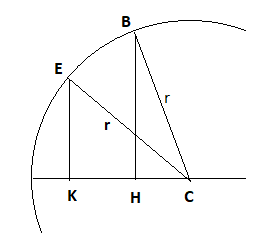
***Image recadrée***
Bonjour
La hauteur cherchée est BE'
BE'=BH-EK
Calculons BH et EK
Soit BHC est triangle rectangle
Sin B=BH/r
BH=sinB*r
Considérons le triangle rectangle EKC
On sait que la bissectrice coupe un angle en deux angles de même mesure
Donc l angle ECK= l angle ECB=y
Siny=EK/r
Ek=siny*r
BE'=sinB*r-siny*r
BE'=rsin(B-y)
La hauteur cherchée est BE'
BE=BH-EK
Calculons BH et EK
BHC est triangle rectangle
Sin B=BH/r
BH=sinB*r
oui
Considérons le triangle rectangle EKC
oui
On sait que la bissectrice coupe un angle en deux angles de même mesure
Donc l angle ECK= l angle ECB=y
Siny=EK/r
Ek=siny*r
BE'=sinB*r-siny*r
BE'=rsin(B-y)
non
=75° (angle BCK)
=45° (angle ECB )
donc l'angle ECK = 75-45 = 30° et ne vaut donc pas l'angle ECB
dans le triangle rectangle EKC il suffit d'écrire:
EK = r sin(
-)
et donc
h = BE = BH-EK = r sin
- r sin(-) Question3
Appliquons le théorème du centre d inertie
P+RN=ma
Projections dans la bas de frenet (s,z,n)
P(px=psin(B-y), pn=Pcos(B-y))
RN( RX=0 , Rn=-Rn)=ma(AX=DV/DT,an=VE^2/R
On a
Pcos(B-y)-Rn=m*VE^2/R
Rn=Pcos(B-y)-m*VE^2/R
Rn=m[gcos(B-y)-(]2gr(siny-sin(B-y)+2l(gsina-f/m)/r]
Question 3:
C'est presque ça: il faut revoir la projection du poids sur la normale et revoir l'expression de Rn
Rn= mg sin(B-) - mVE2/r
En E la bille quitte la piste (elle décolle) donc que vaut la réaction du support R ?
RN=mgsin(B-y)-m*VE^2/r
O=m[gsin(B-y)-VE^2/r]
gsin(B-y)-VE^2/r =0 posons T=B-y
gsinT-VE^2/r=0
-VE^2/r=-gsinT
VE^2=grsinT
2(gr(siny-sinT)+2l(gsina-f/m)=grsinT
2grsiny-2grsinT-grsinT+2l(gsina-f/m)=0
2grsiny-3grsinT+2l(gsina-f/m)=0
2l(gsina-f/m)=3grsinT-2grsiny
[
gsina-f/m=gr(3sinT-2siny)/2l
gsina-gr(3sinT-2siny)/2l=f/m
g[sina-r(3sinT-2siny)/2]=f/m
Je suis bloqué
m =f/g[sina-(rsinT-2siny)/2l]
m=0,2/9,8(0,5-3*sin45-2*sin30)/2l]
m=0,2/9,8(0,5-3*√2/2-2*0.5)/4
m=0,2/9,8(0,5-0,28)
m=0,2/9,8*0,22
m=0,2/2,156
m=0,093 kg
VE=√2[gr(siny-sin(B-y)) +l(gsina-f/m)]
Étourderie!
VE=√2[gr(sin
-sin(-)) +l(gsina-f/m)]Il faut corriger VE comme indiqué juste au-dessus
Et refaire les calculs
C'est: sin - sin(-)
Et non pas: sin - sin(-)
m=f/gsina- 3grsin45-2gsinB/2l
m=0,2/9,8*0,5- 3*9,8*sin45-2*9,8*sin75/4
m=0.2/4,9-0,46
m=0,2/4,44
m=0,045 kg
Recapitulons
2.1) VB2= 2gl sin a - 2Fl/m
2.2) VE2= VB2+ 2gr(sin - sin(-))
3) Rn = mg sin(-) - mVE2/r
4) Rn=0 en E
Donc VE2= g r sin(-)
VB2+ 2gr(sin - sin(-)) = g r sin(-)
2gl sin a - 2Fl/m + 2gr(sin - sin(-)) = g r sin(-
2Fl/m = 2gl sin a + 2gr sin - 3gr sin(-))
Sauf etourderie
Je te laisse terminer
m=2F*l/2glsina+2grsinB-3grsin30
2F*l=2*0,2*2=0,8
2glsina+2grsinB-3grsin30=2*9,8*2*sin30+2*9,8*sin75-3*9,8*sin30=23,83
m=0,8/23,83
m=0,033 Kg
33g,
Aucune des billes indiquees ne convient, cest curieux
Verifie les donnees de ton enonces (l,r,les angles...)
B=l'angle BCD =75° et y=l'angle ECB=45°
Tu es sûr de ces angles, ça ne correspond pas au dessin
non, avec = 45° et = 75° je trouve 33g aussi
mais comme je l'ai déjà dit, je ne pense pas que ce soit les bonnes valeurs (surtout pour )
ou alors il y a encore une erreur de calcul quelque part...
tu verras avec ton prof.
l'essentiel est que tu aies bien compris la démarche à suivre (questions 1,2,3)
ca te servira dans les autres exos.
Bonjour,
Probablement pas d'erreur de calcul : J'ai moi aussi trouvé 33g en enchainant les calculs de manière différente.
Avec une masse de 33g, et une force de frottement constante de 0,2N il me semble bien que la bille ne quitte jamais le point A !
Bonjour odbugt1,
Merci d'avoir refait les calculs, ça me rassure 
Si on prend par ex. =25° (au lieu de 45°) on trouve 50g
Erreur d' énoncé (ou énoncé mal lu)
Bonjour,
Probablement pas d'erreur de calcul : J'ai moi aussi trouvé 33g en enchainant les calculs de manière différente.
Avec une masse de 33g, et une force de frottement constante de 0,2N il me semble bien que la bille ne quitte jamais le point A !
Bonsoir , comment vous avez fait pour trouver cette force de frottement ? Et pourquoi la bille ne quitte jamais le point A ?
Annuler
connectez vous