Inscription / Connexion Nouveau Sujet
Calcul tensions câbles
Bonsoir à tous, j'aimerais savoir comment calculer les tensions de cables formant un triangle isocèle, merci d'avance. Voilà l'exercice :
On maintient en équilibre un cube de masse m à l'aide du dispositif suivant en exerçant une force
sur le câble IJ :
Calculer :
les tensions dans les câbles ED et DF.
les tensions dans les câbles AC et AB
Données :
Masse du cube : m = 50 kg
Valeurs des angles : α = 30° ; β = 45° ; γ = 45°
Pesanteur terrestre : g = 9,8 N.kg-1
Pour l'instant j'ai trouvé les tensions des câbles AC et AB qui sont les suivantes :
= P * cos45 = (50*9.8) * 0.71 = 347.9 N
= P * cos30= (50*9.8) * 0.87 = 426.3 N
Est-ce que pour les câbles ED et DF c'est la même solution, ou est-ce qu'il un cas particulier lorsque les câbles forment un triangle isocèle ?
Merci d'avance.
Il faudrait que tu écrives que la résultante des tensions TAB et TAC est verticale et est égale à la somme des composantes verticales des deux tensions.
Apparemment, ce n'est pas ce que tu as écrit.
La masse m est en équilibre et donc la résultante vectorielle des forces agissant sur l'objet de masse m est nulle.
Avec T3 la tension dans le brin DE et T4 la tension dans le brin DF et P le poids du cube.
T3.cos(gamma) = T4.cos(gamma) --> T3 = T4 (projection sur un axe horizontal)
T3.sin(gamma) + T4.sin(gamma) = P (projection sur un axe vertical)
T3 = T4 = mg/(2.sin(gamma)) = 346 N (arrondi)
-----
Le point A est en équilibre et donc la résultante vectorielle des forces agissant en A et nulle.
Avec T1 la tension dans le brin AB et T2 la tension dans le brin AC
T1.sin(alpha) + T2.sin(beta) = P (projection sur un axe vertical)
T1.cos(alpha) = T2.cos(beta) (projection sur un axe horizontal)
T1.sin(30°) + T2.sin(45°) = 50*9,8
T1.cos(30°) = T2.cos(45°)
(1/2).T1 + T2/V2 = 50*9,8
T1.(V3)/2) = T2/V2
T1 = 359 N (arrondi)
T2 = 439 N (arrondi)
-----
Recopier sans comprendre est inutile.
Sauf distraction. 
Bonsoir J-P, tout d'abord merci pour ce gros coup de main. Comme je le préssentais, il y avait un lien entre les 2 angles du triangle isocèle.
Pour les 2 autres tensions, pour T1 tu as divisé P/ (sin30+cos30) pour trouver 359 N mais par contre pour T2 je ne vois pas du tout comment tu as trouvé ce résultat.
Merci d'avance.
Ou je me méprends sur ce que tu écris ... ou bien tu n'as rien compris de ce que j'ai fait.
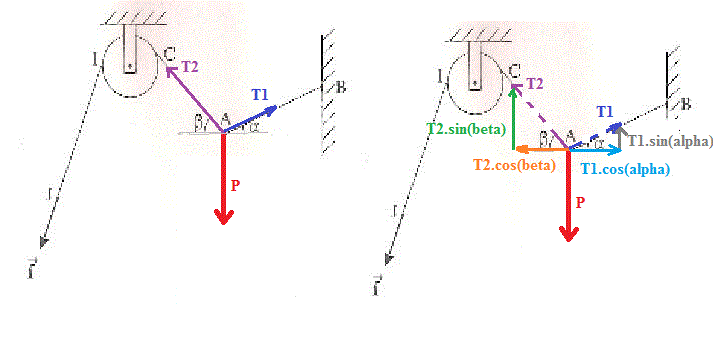
Le point A est soumis à 3 forces P; T1 et T2 (dessin de gauche)
Comme ce point est à l'équilibre (il ne bouge pas), c'est que (1)
On peut décomposer T1 et T2 en leurs composantes horizontales et verticales (dessin de droite).
Par (1), on sait que la somme des composantes verticales de ,
,
est nulle --->
P - T1.sin(alpha) - T2.sin(beta) = 0 (2) (ici, P, T1 et T2 sont les normes des vecteurs)
Par (1), on sait que la somme des composantes horizontales de ,
,
est nulle --->
T1.cos(alpha) - T2.cos(beta) = 0 (3) (ici, T1 et T2 sont les normes des vecteurs)
On a donc le système (1), (2), soit :
P - T1.sin(alpha) - T2.sin(beta) = 0
T1.cos(alpha) - T2.cos(beta) = 0
C'est un système de 2 équations à 2 inconnues (T1 et T2), tout le reste est connu (soit P, alpha et beta)
Et ce système résolu donne : T1 = 359 N et T2 = 439 N.
Sauf distraction. 


