Inscription / Connexion Nouveau Sujet
Calcul de l'énergie cinétique Ec.
Bonsoir , veuillez m'aider s'il vous plaît.
Merci d'avance .
Calcule l'énergie cinétique dans les cas suivants :
1) Un électron de masse 9,11.10-³¹ Kg tournant à la vitesse de 5.10¹6 rad/s , à une distance de 44.10-¹² m du noyau de l'atome . Donnée J∆=mR².
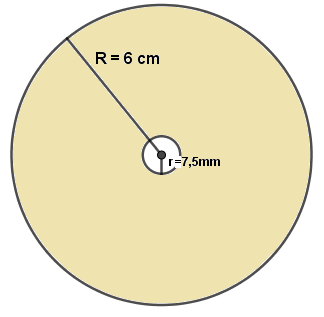
2) Un disque compact de masse 15 g et de rayon 6cm par rapport à son axe , tournant autour de cet axe à la vitesse de 20,33 rad/s . Tu tiendras compte de ce que le disque continent un creux de rayon 7,5 mm autour de son axe.
Donnée : J∆=mR².
Bonsoir,
Aide toi, le ciel t'aidera ...
En d'autres termes et en application des règles de ce forum que tu commences à connaître, il te faut exposer le fruit de tes recherches pour recevoir de l'aide.
C'est ce que je suis entrain de faire en -ce- moment
C'est l'inertie du moment? ou le moment d'inertie? Blague nulle j'en conviens, mais aussi une aide pour trouver où aller voir dans le cours
Je vous laisse bosser

Voici ce que j'ai trouvé .
1) On a le moment d'inertie J∆=mR² or l'expression de l'énergie cinétique est :Ec= ×J∆×
 ² et J∆=mR² d'où Ec=
² et J∆=mR² d'où Ec= ×mR²×
 ²
²
AN: m=9,11.10-³¹ kg ; R=44.10-¹²m ==>R²=1,936.10-21m² et
 ² =5,1.10¹6
² =5,1.10¹6
Donc Ec=
×9,11.10-³¹×1,936.10-21×5,1.10¹6
Ec= 4,49.10-³5 J.
Il semble que l'énoncé donne pour la vitesse (angulaire) de l'électron la valeur de 5 . 1016 rad/s
Si  = 5 . 1016 rad/s alors
= 5 . 1016 rad/s alors  ² = 2,5 . 1033 rad²/s² et pas 5,1 . 1016 comme tu l'as écrit.
² = 2,5 . 1033 rad²/s² et pas 5,1 . 1016 comme tu l'as écrit.
Je suppose qu'à la place de 2,2-18 J on doit lire 2,2 . 10-18 J
Et en effet Ec = 2,2 . 10-18 J est la réponse exacte.
Oui c'est çà .
2) Le moment d'inertie J∆=mR²
Or Ec=×J∆×
 ²
²
EC=×mR²
AN: on a la masse m =15g ==>m=0,015kg ; R=6cm==>R=0,06m R²=3,6.10-3m²;  =20,33rad/s ==>
=20,33rad/s ==> ²=413,3rad²/s²
²=413,3rad²/s²
C'est quoi le creux du rayon de 7,5mm? J'ai un petit problème ici , aidez moi s'il vous plaît ?
Le moment d'inertie d'un disque plein de masse M, de rayon R par rapport à son axe de révolution est comme tu le sais égal à :
On ne peut pas appliquer cette relation à un disque de masse M, de rayon R présentant en son centre une ouverture circulaire de rayon r
Il est indispensable de connaître ou de démontrer la relation qui donne le moment d'inertie d'un tel disque.
Je ne peux rien faire d'autre que de répéter (en le résumant) le contenu de mon post du 22-12-19 à 23:37
J = (1/2) * MR² est une formule qui s'applique à un disque plein.
Le disque compact de cet exercice n'est pas un disque plein.
Donc tu ne peux pas utiliser la formule J = (1/2) * MR²
Je ne peux rien faire d'autre que de répéter (en le résumant) le contenu de mon post du 22-12-19 à 23:20
Hello
Pour utiliser la donnée founie et ne pas passer par le calcul direct, je proposerais bien ceci:
La masse surfacique du disque est
Le moment d'inertie du CD est la différence entre:
- celui d'un disque plein (de même masse surfacique) et de rayon avec
- celui d'un disque plein (de même masse surfacique) et de rayon r avec
Donc
Il fallait bien sûr lire
Le moment d'inertie du CD est la différence entre:
- celui d'un disque plein (de même masse surfacique) et de rayon R:
- celui d'un disque plein (de même masse surfacique) et de rayon r :
Bonjour Dirac,
Tu me coupes l'herbe sous les pieds !
J'avais l'intention, une fois qu'Othniel2 aurait compris pourquoi il ne pouvait pas confondre un disque plein avec un disque évidé, de lui demander s'il n'y avait pas dans son cours un formulaire fournissant une solution à son problème.
Dans la négative j'avais préparé, et je lui aurais proposé une démonstration proche de la tienne, sans toutefois introduire le terme de masse surfacique.
@Othniel2
Comme indiqué par Dirac, le moment d'inertie du disque compact ne se calcule pas par la relation
J = (1/2) * M * R² mais bien par la relation J = (1/2) * M ( R² + r²)
Hello odbugt1!
Oooppps! désolé 
Surtout qu'à cette époque l'herbe ne repousse pas si vite.
Je sais qu'il est assez désagréable de se faire court circuiter lorsque l'on est en train de faire cheminer un étudiant/lycéen sur un certain raisonnement, donc je bats ma coulpe très sincèrement
(je suis preneur de la solution sans masse surfacique à titre perso, j'ai cherché à l'éviter sans y parvenir)
@dirac
Soit " X " la masse du disque s'il était plein et " x " celle de la portion de rayon " r "
(toujours si le disque était plein)
M = X - x
X = π ρ e R² ; x = π ρ e r² avec " ρ " la masse volumique et " e " l'épaisseur du disque
X / R² = x / r² = (X - x) / (R² - r²) = M / (R² - r²)
X = MR² / (R² - r²) ; x = mR² / (R² - r²)
J = J1 - J2 = (1/2) XR² - (1/2)xr²
En remplaçant X et x par leurs expressions précédemment établies on obtient :
J = (M/2) * (R4 - r4) / (R² - r²) = (M/2) * (R² + r²)
X = MR² / (R² - r²) ; x = mR² / (R² - r²)
Désolé pour la faute de frappe (corrigée ci-dessous)
X = MR² / (R² - r²) ; x = Mr² / (R² - r²)
Salut à vous trois,
C'est marrant, je n'ai pas souvenir que les exercices de premières étaient aussi élaborés sur ce chapitre, pour une fois que les programmes me donnent l'impression d'évoluer dans le bon sens 
Bonjour à tous, bonjour gbm
hum....je crois savoir que le posteur n'est pas scolarisé, et qu'il pose des questions en fonction de ce qu'il trouve ça et là....je lui ai indiqué en maths qu'il ne suivait pas du tout les programmes enseignés....
@dirac
Soit " X " la masse du disque s'il était plein et " x " celle de la portion de rayon " r "
(toujours si le disque était plein)
M = X - x
X = π ρ e R² ; x = π ρ e r² avec " ρ " la masse volumique et " e " l'épaisseur du disque
X / R² = x / r² = (X - x) / (R² - r²) = M / (R² - r²)
X = MR² / (R² - r²) ; x = mR² / (R² - r²)
J = J1 - J2 = (1/2) XR² - (1/2)xr²
En remplaçant X et x par leurs expressions précédemment établies on obtient :
J = (M/2) * (R4 - r4) / (R² - r²) = (M/2) * (R² + r²)
Cependant j'ai remplacé simplement l'expression de J∆ que vous avez trouvé suite à votre calcul (que je ne comprends pas ...)
Voici ce que çà donne :
Ec=
 ²
²
An: la masse M du CD =15g = 0,015Kg ; le rayon du CD : R=6cm=0,06m ==>R²=3,6.10-3 ; la vitesse angulaire
 =20,33rad/s ==>
=20,33rad/s ==>  ²=413,3rad²/s² ; le rayon du creux r =7,5mm =0,0075m ==>r²=5,625.10-5m².
²=413,3rad²/s² ; le rayon du creux r =7,5mm =0,0075m ==>r²=5,625.10-5m².
Ec=
 ² <==>
² <==>
Ec=
Ec=0,02J
Merci.
J= (M/2) * (R² + r²)
Ec = (1/2) J ω² = (1/2) * (M/2) * (R² + r²) * ω² = (M/4) * (R² + r²) * ω²
avec
M = 15.10-3 kg
R = 6.10-2 m
r = 7,5.10-3 m
ω = 20,33 rad/s
j'ai trouvé Ec = 5,67.10-3J
Et si tu désires des compléments pour t'aider dans ce que tu ne comprends pas, il te faut poser des questions précises.
OK , Au niveau de 9h56 ,
Comment faite vous pour passer de là
M = X - x
X = π ρ e R² ; x = π ρ e r² avec " ρ " la masse volumique et " e " l'épaisseur du disque
X / R² = x / r² = (X - x) / (R² - r²) = M / (R² - r²)
X = MR² / (R² - r²) ; x = mR² / (R² - r²)
X = π ρ e R² donne X / R² = π ρ e
x = π ρ e r² donne x / r² = π ρ e
Donc X / R² = x / r²
Lorsque 2 fractions A/B et C/D sont égales elles sont aussi égales à une troisième fraction (A - C) / (B - D ) ayant pour numérateur la différence des numérateurs et comme dénominateur la différence des dénominateurs.
Donc X / R² = x / r² = (X - x) / (R² - r²)
Et comme X - x = M on obtient
d'une part X / R² = M / (R² - r²) dont on retire X = MR² / (R² - r²)
et d'autre part x / r² = M / (R² - r²) dont on retire x = Mr² / (R² - r²)

 toujours pareil .
toujours pareil .
