Inscription / Connexion Nouveau Sujet
Calcul à l'instant t
Bonjour je bloque sur la dernière question de ce exercice, merci de m'aider
ÉNONCÉ
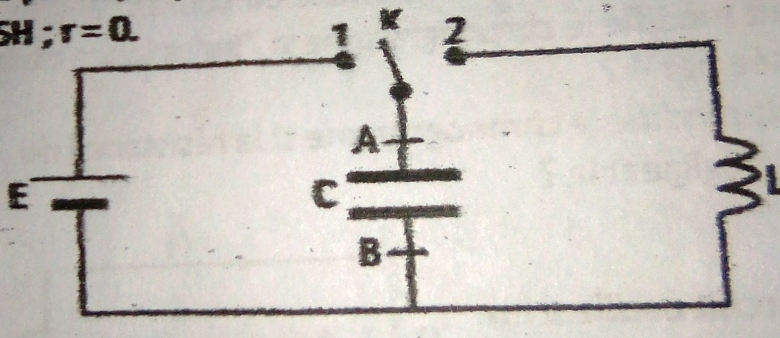
On réalise le montage selon la figure ci-dessous.
Données numériques : f.é.m. du générateur : E=12V ; r=0 ; Capacité : C=1,5µF ; Auto-inductance : L=0,55H, r=0
1. On ferme l'interrupteur en position 1.
Quelles sont la tension aux bornes du condensateur, la charge
et l'énergie
du condensateur en fin de charge ?
= E =12 V
=
/ C
= 1,8.10^-5 C
= ½(
/ C)
= 1,08.10^-4 J
2. Ensuite on ferme l'interrupteur en position 2 à l'instant choisi comme origine des dates.
2-1- Etablir l'équation différentielle du circuit oscillant. Calculer la pulsation propre ωo de ce circuit
Equation différentielle : q" + 1/(LC) q = 0
ωo = 1/ √(LC) ωo = 1101 rad/s
2-2- Donner les expressions de q(t), charge du condensateur, et i(t), intensité du courant.
Je trouve :
q(t) = 1,8.10^(-5)Cos(1101t) et i(t) = -1,98.10^(-2)Sin(1101t)
2-3- Donner les expressions des énergies stockées à chaque instant dans le condensateur et dans la bobine.
Ec(t) = 1,08.10^(-4)Cos²(1101t) et Eb(t) = 1,08.10^(-4)Sin²(1101t)
Calculer ces énergies aux instants données ci-dessous en complétant le tableau. Conclus
(Je bloque sur cette question)
| t (s) | 0 | T/8 | T/4 | T/2 |
| Ec (J) | ||||
| Eb (J) | ||||
| EC + Eb (J) |
Exactement, en fait ce que je trouve la correction trouve le contraire
Avant de donner les résultats je trouve T = 5,71.10^-3
J'ai oublié l'unité en seconde
1ere Case t=0s
Ec = Eb = 1,08.10^-4 J
2e case t= T/8 donc t=7,14.10^-4S
Uc = 5,4.10^-5 J
Ub = 5,41.10^-5 J
Aux arrondis de calculs près, ton résultat est correct mais on peut faire beaucoup plus simple et rapide. Je prends le cas de Ec et je te laisserai ensuite généraliser. Il suffit de remarquer :
En t=T/8 cela donne :
Ah oui c'est vrai que c'est plus simple de calculer avec les π
Merci beaucoup j'envoie toutes mes réponses alors
| t (s) | 0 | T/8 | T/4 | T/2 |
| Ec (J) | 1,08.10^-4 | 5,4.10^-5 | 0 | 1,08.10^-4 |
| Eb (J) | 0 | 5,4.10^-5 | 1,08.10^-4 | 0 |
| EC + Eb (J) | 1,08.10^-4 | 1,08.10^-4 | 1,08.10^-4 | 1,08.10^-4 |
Conclusion : L'energie Totale dans le circuit se conserve à chaque instant .



