Inscription / Connexion Nouveau Sujet
caisse suspendue par deux cables
bonjour jai cet exercices en DM pour lundi pouvais-vouz m'aidez s'il vous plait je coince =)
voici le sujet:
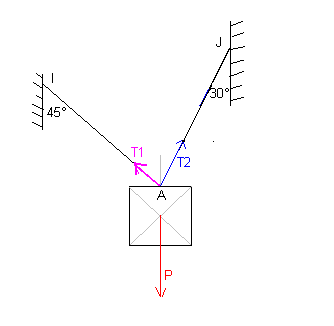
Une caisse cubique, d'arête a= 50 cm, supposée homogène et de masse m= 300kg, est en équilibre . Au centre A de sa face supérieure sont fixés deux cable de longueurs égales et de masses négligeable, leurs seconde extrémités étant reliées à 2 supports verticaux en I et J. Les cables forment avec leurs supports verticaux des angles: alpha= 45° et béta= 30°
1) faire le bilan des forces qui s'exercent sur la caisse. Peut-on négliger la poussée d'archimède due à l'air ?
2) représenter les forces que l'on ne peut pas négliger, en respectant leur direction , sens et point d'application.
3) Donner les expréssions littérales et les valeurs de ces forces.
4) Donner les caractéristiques de la force exercée par le mur sur le cable au pont I. Justifier.
En attende d'un réponse je vous remercie d'avance =)
pour la 1ere jai mis : le poid puis la force de tension de cables
puis que l'on pouvait négliger la poussée d'archimède
pour la 2) je pense que jai bien représenter (je n'arrive pas a mettre des shéma dsl)
pour la 3) je ne sais pas par ou commencer et la 4) meme chose
Merci.
Volume de la boîte = 0,5³ = 0,125 m³
masse volumique de la boîte = 300/0,125 = 2400 kg/m³
Rho boite > > > Rho air et donc on peut négliger la la poussée d'archimède due à l'air par rapport au poids de la boîte.
---
Bilan des forces sur la boîte:
- Poids de la boîte (vertical cers le bas)
- Poussée d'Archimède de l'air sur la boîte (vertival vers le haut, négligeable devant le poids de la boîte.)
- Taction dans les 2 cordes (dans la direction des cordes, cers le haut).
---
P = mg = 300 * 9,81 = 2943 N
-----
-----
La boîte est en équilibre et donc la somme vectorielle de P;, T1 et T2 est nulle.
Par projection sur un axe horizontal:
T1.cos(45°) - T2.cos(60°) = 0
T1/V2 - T2/2 = 0 (avec V pour racine carrée)
T1 = T2/V2
Par projection sur un axe vertical:
T1.sin(45°) + T2.sin(60°) = P
T1/V2 + T2*(V3)/2 = mg
(T2/V2)/V2 + T2*(V3)/2 = mg
T2/2 + T2*(V3)/2 = mg
T2(1+V3) = 2.mg
T2 = 2mg/(1+V3)
T1 = T2/V2
T1 = V2 . mg/(1+V3)
T1 = V2 * 2943 /(1+V3) = 1523 N
T2 = 2 * 2943 /(1+V3) = 2154 N
-----
Et les cordes étant en équilibre:
Force du mur sur le câble en I:
Direction de AI, vers le haut et norme = |T1| = 1523 N
Force du mur sur le câble en J:
Direction de AJ, vers le haut et norme = |T2| = 2154 N
-----
Sauf distraction. 
Merci pour votre réponse mais je voudrais juste savoir pourquoi T1 vous le divisez pas (racine carré) V2 et pareil pour V3 .
Dites moi une explication s'il vous plait.
Merci d'avance.
T1.sin(45°) + T2.sin(60°) = P
Or sin(45°) = 1/V2 et sin(60°) = (V3)/2
--> T1 * 1/V2 + T2 * (V3)/2 = P
T1/V2 + T2 * (V3)/2 = P




