Inscription / Connexion Nouveau Sujet
Association de deux piles en dérivation
Bonjour !!
J'ai juste une question a vous posez pour connaitre Eeq, je ne vois pas quel loi il faut utiliser :s
Voici l'énoncé :
Une pile de f.é.m. E1=4.5V et de résistance interne R1=1.2
est monté en dérivation aux bornes d'une autre pile de f.é.m. E2=3V et de résistance interne R2=0.8. Soit U la tension aux bornes de l'ensemble des deux piles.
Voici la question :
Après avoir appliqué la loi des nœuds, exprimer la tension U en fonction de l'intensité totale I. Montrer que les deux piles sont équivalentes à une f.é.m. Eeq= 3.6V et de résistance interne Req=0.48
Pour la résistance équivalente il suffit d'utiliser la loi d'additivité des conductances dans un circuit électrique en dérivation. Cela nous donne bien Req=0.48
Mais pour Eeq, je ne vois pas quelle loi, il faut utiliser.
Si quelqu'un peut me mettre sur la voie ! Cela serait fort sympathique !! 
Merci d'avance !!
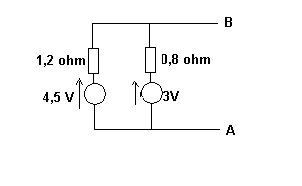
Tension U(AB) si on laisse le circuit extérieur AB ouvert.
I = (4,5-3)/(1,2+0,8) = 0,75 A
U(AB) = 3 + 0,8 * 0,75 = 3,6 V
-----
Courant dans un court-circuit qui serait fait entre A et B:
I' = 4,5/1,2 + 3/0,8 = 7,5 A
-----
Résistance série qui limite le courant à 7,5 A avec une source de tension de 3,6 V:
R = 3,6/7,5 = 0,48 ohm
-----
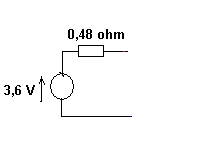
--> le circuit équivalent est un générateur de E = 3,6 V et de résisances internes = 0,48 ohm.
-----
C'est l'équivalent Thévenin du circuit.
Sauf distraction. 
Eh bah, j'en apprend des choses sur ce site
Merci de votre aide !!
Mais juste une dernière question si à la place d'ouvrir le circuit on rajoute une résistance R de 2.4
Alors on aura :
I= Eeq / ( Req + R )
= 3.6 / ( 0.48 + 2.4 )
= 3.6 / 2.88
= 1.25 A
Le circuit équivalent pour la initiale est :
Si on le charge par une résistance de 2,4 ohms, on a:
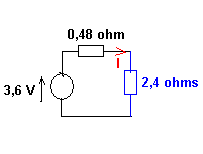
Le courant dans la charge est I = 3,6(0,48 + 2,4) = 1,25 A.
La tension aux bornes de la résistance de charge est : 2,4 * 1,25 = 3 V.
-----
Sauf distraction.
Annuler
connectez vous