Inscription / Connexion Nouveau Sujet
Association d'un condensateur et d'une bobine
Bonjour à tous,
Je bloque sur les premières questions d'un exercice.
Voici l'énoncé:
On réalise le montage schématisé ci-dessous.
Le condensateur de capacité C est initialement chargé avec un générateur de tension
(UG = E).
On choisit comme instant initial le moment où on ferme l'interrupteur K.
La tension aux bornes de la capacité est donc, à l'instant t = 0, égale à E = 5,0 V.
La bobine d'inductance L = 1,0 H a une résistance interne négligeable. Ainsi on considère
que la résistance totale du circuit est négligeable.
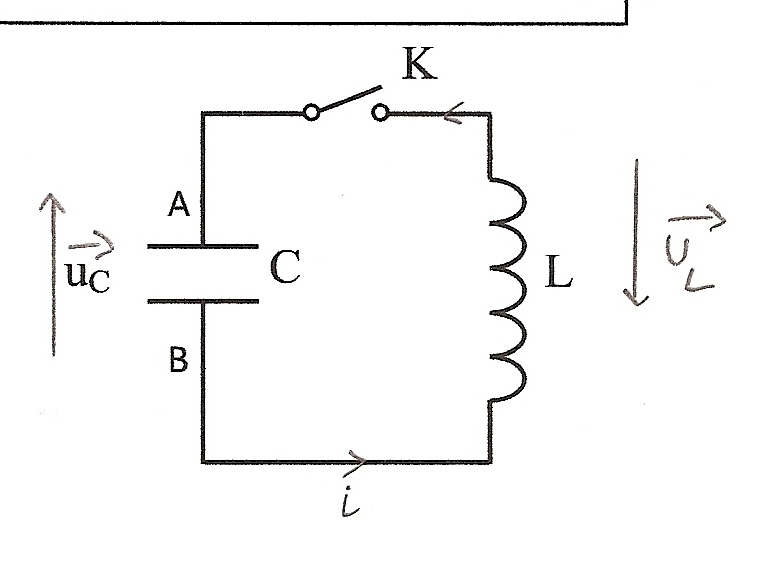
1. Introduire sur le schéma (à refaire sur la copie) le sens du courant
conventionnel que vous utiliserez pour la suite.
2. Que vaut l'intensité du courant dans le circuit à l'instant t = 0 ? Justifier.
3. En utilisant le sens du courant introduit, représenter sur le schéma les tensions
uL et uC.
4. Quel est l'armature positive (conventionnel) correspondant au sens du courant conventionnel introduit ?
5. Représenter sur le schéma l'entrée Y1 et la masse de l'oscilloscope à mémoire, pour mesurer l'évolution de uC au cours du temps.
Pour la question 2, i=0
Pour la question 4, l'armature positive est l'armature A
Pour la question 5, je pensais placer la masse dans l'angle en dessous du point B et l'entrée Y1 sur le point A
Merci de vos réponses
2)
Le courant dans une inductance ne peut pas varier instantanément.
Comme i = 0 juste avant la fermeture de K, il vaut encore 0 jste après la fermeture de K.
--> i(0) = 0
-----

Merci 
Plus on me donne une solution de l'equa diff a demontrer ( c'est fait), la solution est Uc = Um.sin(2 .(t/T0)+
.(t/T0)+ 0)
0)
On me demande de determiner l'expression de Um, T0 et  0
0
Pas de problèmes pour les deux premiers mais je bloque sur  0
0
Vous avez une idée ?
uc = Um.sin(2Pi.t/To + Phi0)
uc(0) = 5 --> Um.sin(Phi0) = 5
i = C.duc/dt
i = C.Um.2Pi/To.cos(2Pi.t/To + Phi0)
i(0) = 0 --> cos(Phi0) = 0 --> Phi0 = Pi/2
...




