Inscription / Connexion Nouveau Sujet
Applications des bases de la dynamique n°1
Bonjour
J'aurais besoin d'aide pour cet exercice.
Merci de me guider chers amis 
L'énoncé :
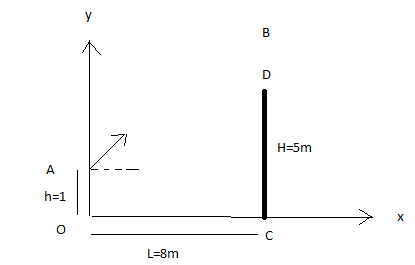
Un projectile considéré comme ponctuel est lancé,dans le champ de pesanteur ,à partir d'un point A situé à la distance h= 1 m du sol ,avec une vitesse faisant un angle  avec l'horizontale et de valeur V0= 16 m/s.
avec l'horizontale et de valeur V0= 16 m/s.
Un mur de hauteur H= 5 m est disposé à la distance L= 8 m du lanceur .
1) Établir l'équation du mouvement du projectile dans le repère (O,i,j)
2) Établir l'équation cartésienne de la trajectoire du projectile. Quelle est sa nature?
3) Entre quelles valeurs doit être compris l'angle  pour que le projectile passe au-dessus du mur ?
pour que le projectile passe au-dessus du mur ?
4) On fixe la valeur de  à 45°.
à 45°.
a. Soit B le point de passage du projectile au-dessus du mur.Calculer la distance d séparant le sommet du mur au point B.
b. Soit VB la vitesse du projectile au point B .
Notons  l'angle formé par la vitesse
l'angle formé par la vitesse et l'horizontale
 = (Ox,
= (Ox, ). Calculer
 .
.
Ma réponse :
2)
On a
Si c'est juste merci de me guider pour la 3
Je vais poster la figure
Bonjour,
L'équation cherchée dépend du référentiel et du repère choisi pour étudier le mouvement.
Tu n'as pas précisé ces choix.
Peut être que la figure, si le repère y est présent, permettra d'y voir plus clair.
A défaut de figure je cherche à savoir quelles sont les coordonnées du projectile au moment où il est lancé dans le référentiel (Ox,Oy) qui a été choisi .
OK on a comme système le projectile.
RTSG
BA: P
TCI
En vecteur
P= ma ==> g=a
Au moment où il est lancé :
ay= -g
V0x= V0cos
V0y= V0sin
On en déduit
x= V0t cos
y= -1/2.g t2 V0tsin
D'où l'équation cartésienne
x= V0t cos
y= -1/2.g t2 V0tsin

Si le référentiel est bien celui que je te propose, alors :
y= -1/2 g . t2 +V0 . t .sin(
 ) + h
) + h
car à la date t=0, y(0) = h
L'équation cartésienne est donc :
Pour que le projectile franchisse le mur il suffit que y(L)>H
Il s'agit donc de résoudre cette inéquation, l'inconnue étant l'angle ( )
)
Je cherche des méthodes pour résoudre cette inégalité mais on arrive toujours pas.
On a pu avoir
-cos2 +64sin
+64sin > 32
> 32
Alors, il te faut l'utiliser pour résoudre y(L)>H
Une bonne idée est de résoudre d'abord y(L) = H en substituant dans l'équation cartésienne le terme
en 1/cos²( ) par 1+tan²(
) par 1+tan²( )
)
Tu obtiendras une équation du 2e degré dont l'inconnue est tan( ) et qui admet 2 solutions.
) et qui admet 2 solutions.
Il ne restera plus qu'à passer des solutions de l'équation à ceux de l'inéquation pour trouver l'intervalle cherché.
OK pour l'équation de 2e degré.
Je ne trouve pas les mêmes racines que toi, mais bien entendu j'ai pu faire une erreur et j'ai un peu la flemme de vérifier pour l'instant.
Mais ce n'est pas fini : Il faut répondre à la question telle qu'elle est posée !
OK en posant X= tan(a)
-1,25X2+8X -5,25=0
tan(a)1= 6,23
tan(a)2= 0,1684 ==>
 = 80,80°
= 80,80°
Ou
 = 9,56°
= 9,56°
Je sais pas laquelle des deux valeurs est juste ...
Chaque chose en son temps : j'en suis toujours à la question 3 qui n'a pas été résolue.
je ne trouve toujours pas la même chose que toi pour les racines de l'équation -1,25. X2 +8X -5,25=0
Je secoue ma flemme et je recalcule
Δ = 8² - (4*(-1,25)*(-5.25)) = 64 - 26,25 = 37,75 = 6,14²
Ce qui donne :
 1
1 36,5°
36,5°
 2
2 80,0°
80,0°
Il ne s'agit pas de se demander laquelle des deux valeurs "est juste", mais de revenir à l'inéquation pour trouver la plage de valeurs de l'angle  compatibles avec un franchissement du mur par le projectile
compatibles avec un franchissement du mur par le projectile
Il faut appliquer les règles du signe d'un trinôme :
La règle qui t'intéresse ici est la suivante :
Un trinôme ax²+bx+c qui admet 2 racines réelles distinctes x1 et x2 (x1<x2)
- est du signe de (-a) pour les valeurs de x situées entre x1 et x2
- est du signe de a pour les valeurs de x inférieures à x1 ou supérieures à x2
Ici le trinôme à étudier est
-1,25X2 + 8X - 5,25 qui admet 2 racines X1 = 0,74 et X2 = 5,66
D'après la règle précédente ce trinôme est positif pour les valeurs de X comprises entre 0,74 et 5,66.
Or le trinôme positif correspond à y(L)>H
Donc pour les valeurs de tan( ) comprises entre 0,74 et 5,66 c'est à dire pour les angles
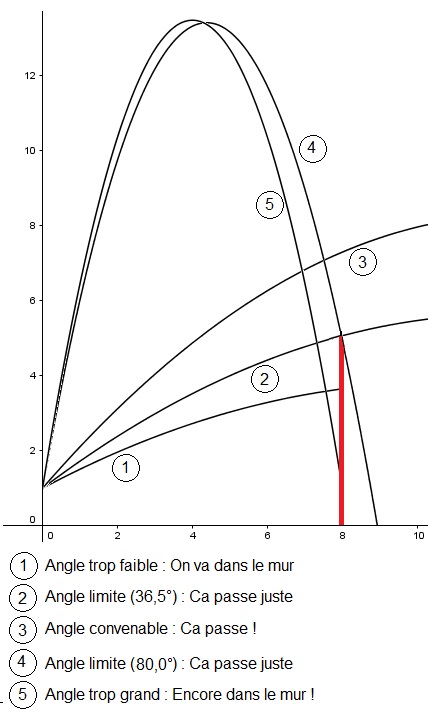
) comprises entre 0,74 et 5,66 c'est à dire pour les angles  compris entre 36,5° et 80° le projectile passe en dessus du mur.
compris entre 36,5° et 80° le projectile passe en dessus du mur.
Conclusion:
Selon l'angle  de lancement du projectile :
de lancement du projectile :
Pour  <36,5° le projectile ne franchit pas le mur
<36,5° le projectile ne franchit pas le mur
Pour  =36,5° le projectile "rase" le haut du mur.
=36,5° le projectile "rase" le haut du mur.
Pour  compris entre 36,5° et 80° le projectile passe en dessus du mur.
compris entre 36,5° et 80° le projectile passe en dessus du mur.
Pour  =80,0° le projectile "rase" le haut du mur.
=80,0° le projectile "rase" le haut du mur.
Pour  >80,0° le projectile ne franchit pas le mur
>80,0° le projectile ne franchit pas le mur