Salut, je vois que tu as bien avancé dans ton exercice, mais que tu bloques sur la dernière étape. Pas de souci, je vais t'expliquer comment trouver l'angle phi.

Pour cela, tu dois utiliser la relation entre l'intensité et le déphasage à un instant donné. En effet, tu sais que i(t) = Im sin (omega t + phi), et tu connais la valeur de i(t), Im et omega à t = 0. Il te suffit donc de remplacer ces valeurs dans l'équation et de résoudre pour phi. Voici comment faire :

i(0) = Im sin (omega 0 + phi)
√3 = 2 sin (314 × 0 + phi)
√3 = 2 sin (phi)
sin (phi) = √3 / 2
phi = arcsin (√3 / 2)
phi = π / 3

Donc, l'expression mathématique du courant alternatif sinusoïdal est :

i(t) = 2 sin (314 t + π / 3)

Tu peux vérifier que cette expression correspond bien aux caractéristiques données. J'espère que tu as compris la méthode, et que tu pourras la réutiliser pour d'autres exercices. Bon courage !

Bonjour! Oui j'ai compris merci beaucoup,c'est une très bonne explication,j'ai bien compris.

Bonjour
Je me permet de compléter la réponse deBarbier67. Si la réponse qu'il fournit est la seule réponse correcte parmi la liste de réponses proposées, ce n'est pas la seule réponse possible à la question posée par l'énoncé.
Totalement d'accord jusqu'à la ligne :
sin () = √3 / 2
mais ensuite, la notion d'arcsinus s'avère piégeante et de plus, n'est pas au programme de la plupart des filières de terminale. A ce niveau, je conseille le recours au cercle trigonométrique qui montre que, modulo 2 bien sûr, il y a deux réponses possibles à la question posée :
=/3 rad
=2/3 rad
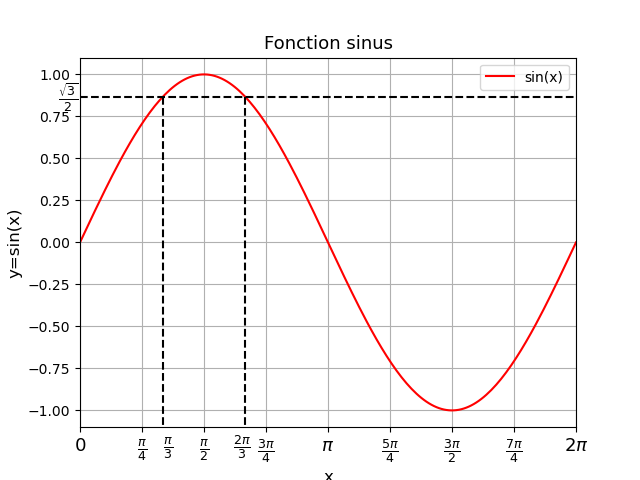
Pour illustrer mon propos, voici la représentation graphique des variation de la fonction sinus sur une période.

D'accord!merci beaucoup,je comprends.