Inscription / Connexion Nouveau Sujet
Action d'un champs magnetique sur un courant
Bonjour, j'espère que vous allez bien 
j'ai un problème pour comprendre l'énoncé si on peut le dire ainsi d'un exercice. Merci d'avance pour votre aide.
Voici l'énoncé.
Une balance est constituée :
-d'un fléau AA' mobile autour d'un axe horizontal (O)
- d'un plateau (P) ;
- d'un petit cadre carré de côté a comportant N spires. Le cadre est fixé par le milieu de l'un des côtés au fléau en A.
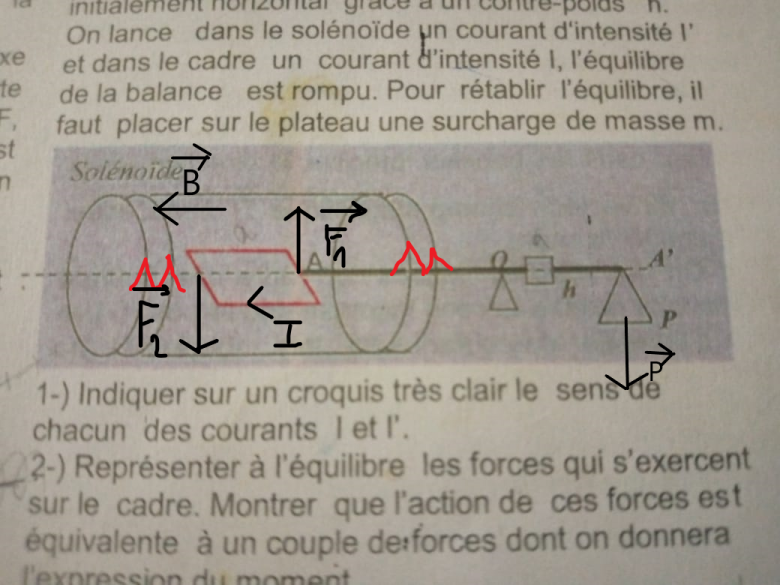
Le plan du cadre est horizontal lorsque le fléau est horizontal.(voir croquis). Le cadre est placé à l'intérieur d'un solénoïde comportant n spires par mètre de longueur. Le fléau, lorsqu'il est horizontal est parallèle à l'axe du solénoïde. Le fléau est initialement horizontal grâce à un contre-poids h.
On lance dans le solénoïde un courant intensité I' et dans le cadre un courant d'intensité I. L'équilibre de la balance est rompu. Pour rétablir l'équilibre, il faut placer sur le plateau une surcharge de masse m.
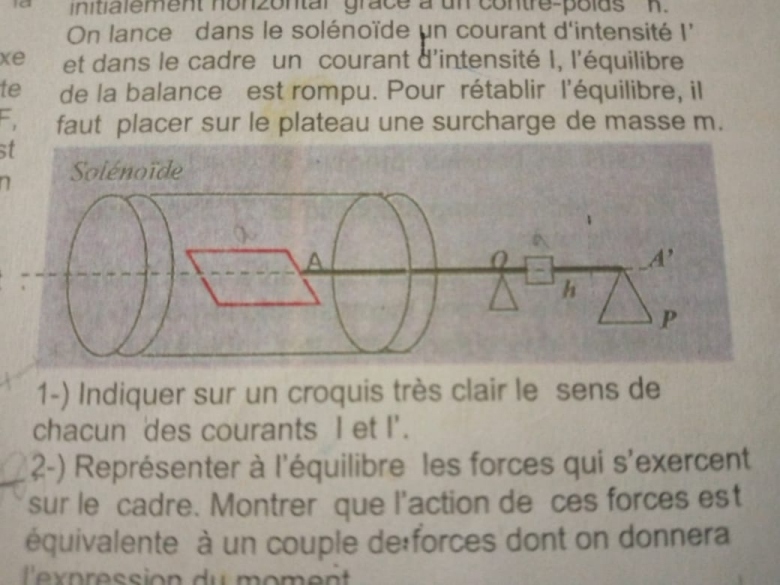
1-) Indiquer sur un croquis très clair le sens de chacun des courants l et l'.
2-) Représenter à l'équilibre les forces qui s'exercent sur le cadre. Montrer que l'action de ces forces est équivalente à un couple de forces dont on donnera l'expression du moment.
3-)Ecrire la condition d'équilibre de la balance en fonction de I, l', N, n,a, m et l (distance OA').
Bonsoir
Qu'as-tu réussi à faire ? Qu'est ce qui te gêne exactement ?
Peux-tu rescanner le schéma en y indiquant les sens des courants ?
Voici mon problème.
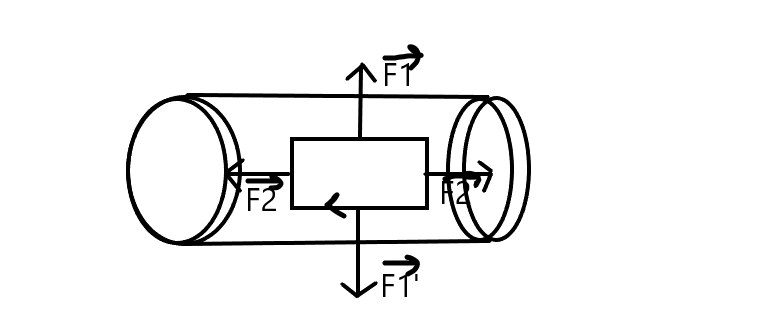
En principe si l'équilibre est rompu et qu'on utilise une surcharge sur le plateau P. Cela signifierait que le solénoïde s'est dirigé vers le bas. En faisant l'inventaire des forces je me retrouve avec des forces qui sont toutes opposées donc en principe il n'y a pas de force qui pourrait dirigé le solénoïde vers le bas non ?
Bonsoir
Qu'as-tu réussi à faire ? Qu'est ce qui te gêne exactement ?
Peux-tu rescanner le schéma en y indiquant les sens des courants ?
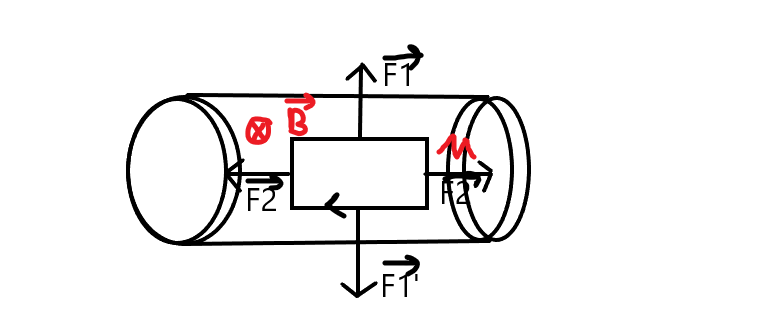
Tu as raison concernant la résultante des forces de Laplace. Mais tu as ici un solide mobile autour d'un axe horizontal fixe passant par O. Il faut donc étudier la somme des moments des différentes forces par rapport à l'axe de rotation.
Attention au schéma. Le vecteur champ magnétique créé par le solénoïde est parallèle à l'axe du solénoïde. Il te faut revoir les forces de Laplace en conséquence et choisir le sens du courant dans le cadre de façon que les moments de ces forces compensent le moment du poids de la surcharge placée sur le plateau.
je vois
J ai un problème
voici mon schéma, sauf que peut importe le sens de I, en haut on aura B
I=0 et les deux forces restantes auront des moments qui vont se compenser j'ai l'impression.
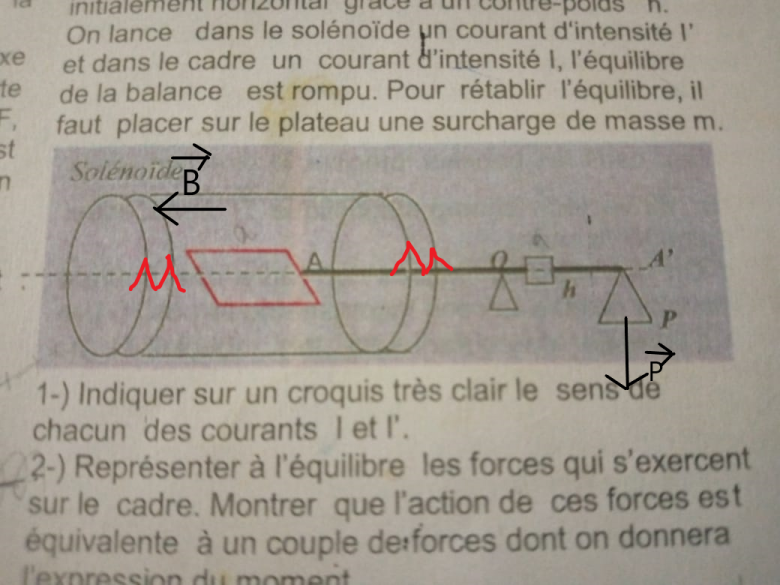
Les forces de Laplace exercées sur les côtés parallèles à l'axe du solénoïde sont effectivement nulles. Pour les deux autres côtés, plus la distance à l'axe de rotation est grande plus le moment par rapport à cet axe est grand. La somme des deux moments n'est donc pas nulle.
Ok je vois. Mais le produit vectoriel de I et B ne doit pas plutôt créer une force verticale sur les cotés lorsqu'on utilise la regle de la main droite ?
Sur les côtés perpendiculaires à l'axe du solénoïde, les forces sont verticales effectivement. Réfléchis aux sens de ces forces pour que leurs actions sur le solide en rotation puisse être compensée par l'ajout d'une surcharge sur le plateau. Cela te donnera le sens du courant dans le cadre rectangulaire.
ohh okok je pense je vois mieux maintenant.
J'ai dans ce cas ce schéma parce que les forces doivent être dirigées vers le bas.
2) Dans le systeme cadre
Bilan des Forces:
A l equilibre: M
(F1)+M(F2)=0
Donc on pourrait assimiler ces forces a un couple car ils ont la même intensité et son de sens opposés
M(C)=F1.(OA+a)-F2.(OA)=IBa2
2) Dans le systeme cadre
Bilan des Forces:
A l equilibre: M
(F1)+M(F2)=0
Donc on pourrait assimiler ces forces a un couple car ils ont la même intensité et son de sens opposés
M
(C)=F1.(OA+a)-F2.(OA)=NIBa2Tu as fait de bonnes choses mais tu as commis quelques erreurs.
Concernant ton dernier schéma : les sens des forces sont corrects mais es-tu sûr du sens du courant dans le cadre.
Ton message du 13-06-24 à 23:07 : C'est la somme des deux vecteurs forces qui est le vecteur nul ; pas la somme des moments. La somme des moments est le moment du couple que tu calcules correctement ensuite mais avec un oubli : chaque force de Laplace vaut N.I.B.a. Tu as apparemment rectifié ensuite. Il te reste à rectifier le résultat final.
Oui vous avez raison pour le sens du courant c'est l'inverse.
Par contre j'ai pas très bien compris. Pourquoi à l'équilibre la somme des moment n'est pas nulle ?
L'équilibre n'est atteint qu'après ajout de la surcharge. C'est donc finalement la somme des moments des trois forces qui est nulle : F1 , F2 et P.
Ta rectification est correcte. Tu as juste un problème de signe dans le moment du poids de la surcharge. Une somme de deux quantités positives ne peut pas être nulle !
Je vois je vois. En partant du principe que c'est le moment d'un couple de forces je peux mettre
3) Condition d'équilibre de la balance
M(P)+M(C)=0
le sens positif est orienté vers le bas
D'où:
D'accord maintenant. En comptant positivement le moment du poids de la surcharge et négativement celui du couple de Laplace, tu choisis comme sens de rotation positif le sens horaire (celui des aiguilles d'une montre). Il serait bien de le préciser sur le schéma par une flèche.
Annuler
connectez vous