Je pense devoir utiliser le theoreme de pythagore mais je sais pas comment y proceder

Bonsoir,

Dans un problème de mécanique, il est toujours utile de faire d'abord un schéma avec un système d'axes.

Ensuite il est nécessaire de faire un bilan des forces et déterminer les coordonnées vectoriels des forces mises en jeu.

Enfin tu peux applique la seconde loi de Newton pour ensuite remonter aux équations de vitesses en effectuant des primitives (ne pas oublier les conditions initiales!).

Bon courage,

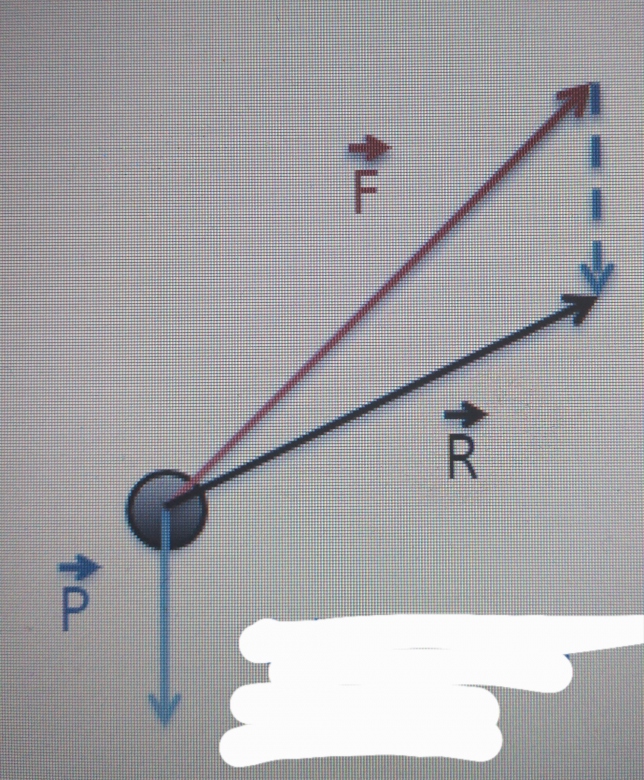
Bonsoir j'ai realisé le schema suivant qui modelise la situation .Donc la sphere est soumise a l'action du poids , la force de lancer et la reaction
Mais je ne sais pas comment trouver les coordonnées vectoriels

Bonsoir,

Avec des axes (x , y) ça devrait t'aider pour déterminer les coordonnées des forces. Par ailleurs que représente le vecteur R ?

Le vecteur R represente la force de reaction de la sphere lors du contact avec la main.
Mais en fait le probleme est que je ne sais pas comment utiliser Pythagore pour pouvoir trouver les coordonnées x et y

Dans ce cas, il n'est pas nécessaire de prendre en compte la force de réaction, on n'a pas de donnée concernant celle ci.

Il n'y a pas besoin de Pythagore ici. J'utiliserais plutôt un système d'axe comme ci-dessous.

Ici tu peux donc exprimer Px, Py, Fx et Fy avec le système d'axe.
Est-ce que tu vois comment faire ?

Je vois pas trop comment faire

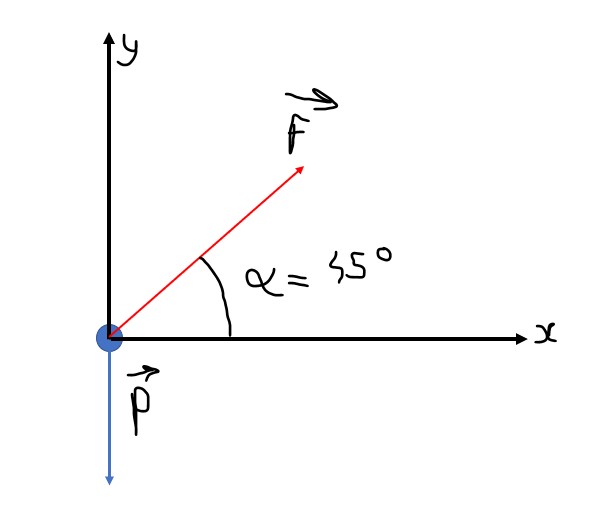
En analysant le système d'axe, tu trouves :
Px = 0
Py = -mg
Fx = Fcos(alpha)
Fy = Fsin(alpha)

Quand tu appliques la deuxième loi de newton tu as :

dvx/dt = ax = Px + Fx
dvy/dt = ay = Py + Fy

Il faut primitiver pour obtenir les expressions des vitesses.

je rectifie mes expressions pour la deuxième loi de Newton :

m.dvx/dt = m.ax = Px + Fx
m.dvy/dt = m.ay = Py + Fy

Mais comment je vais trouver la vitesse a partir de ces deux expressions

Bonjour,

Il faut appliquer une primitive, tu n'as jamais eu d'exercice du même genre ?

Bonjour à tous,

En 1ere, en France, les eleves ne connaissent que la relation approchée suivante:

m /t

La relation differentielle n'est vue qu ' en terminale.

Bonjour krinn,

Merci pour cette précision ! Effectivement je commençais à douter.

La relation suivante est elle aussi au programme de première ?



Merci,

Oui, c'est la formule generale de la norme d'un vecteur, appliquée à (v_x, v_y)

Très bien merci, je voulais m'en assurer

Bonjour
Je me demandais bien parceque on a jamais vu c'est quoi une primitive mais on a deja vu celle ci : v=vx²+vy²

donc a partir de cette formule je peux trouver la valeur du vecteur de R
R=200²+72² = 213 N
Puis je peux faire Δv = R × Δt / m pour trouver la vitesse de la sphere
Mais je ne sais pas si mon raisonnement est bon et si j'ai bien calcule la valeur de R

Bonsoir
Notre proffesseur vient de poster la correction :

Le poids de la sphère a pour valeur P = m × g = 7,3 × 9,8 = 72 N D'après le théorème de Pythagore, la résultante des forces a pour abscisse Rx = 200 / √2 = 141 N et pour ordonnée Ry = 200 / √2 - P = 69 N. Donc la résultante des forces a pour norme R = √(Rx2 +Ry2) = 157 N D'après la 2ème loi de Newton, Δv = R × Δt / m = 157 × 0,5 / 7,3 = 10 m/s

Mais je ne comprends toujours pas d'ou vient l'expression Rx = 200 / √2 = 141 N  et Ry = 200 / √2 - P  

Bonsoir,

En repartant des expressions qu'on a obtenues précédemment :

m.Δvx/Δt  = Px + Fx = 0 + Fcos(45)
m.Δvy/Δt  = Py + Fy  = -mg + Fsin(45)

On obtient :
Δvx = Δt.Fcos(45)/m
Δvy = Δt.Fsin(45)/m  - Δt.g

Or à t=0 , v=0, soit :
vx = t.Fcos(45)/m = 0,5.200.cos(45)/7,3 = 9,7 m/s
vy = t.Fsin(45)/m  - t.g =  0,5.200.sin(45)/7,3 - 0,5.9,81 = 4,8 m/s

En appliquant la relation  v = √(vx^2 +vy^2), on trouve :
v = 10,8 m/s

Précédemment tu évoquais le vecteur R comme la force de réaction, mais attention, ici il s'agit de la résultante des forces soit P + F.

D'après ta correction fournie, il semblerait que le théorème de Pythagore soit utilisé. J'ai un peu du mal à voir les triangles rectangles ici...

Cependant, on a vu précédemment que Rx = Px + Fx = 0 + Fcos(45)
C'est de la trigonométrie, cos(45) = cos(π/4) = √2/2 = 1/√2
Donc Fcos(45) = 200/√2.. On retrouve bien la même chose !

Espérant avoir répondu à l'attente de tes interrogations !

Ah D'accord Merci beaucoup pour ton aide je pense avoir compris