Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Vitesse du skieur

Posté par
modou15 13-12-19 à 12:42

Bonjour j'aimerais que vous m'aidiez à résoudre l'exercice suivant un skieur de Massa m=80g glisse sur un début de piste formée de deux parties AB et BC .la partie AB représente un sixième de son circonférence de rayon r=10m :BC est une petite rectiligne horizontal d'une longueur L=50m tous le trajectoire a lieu dans un même plan vertical le skieur de part A sans vitesse initiale on peut remplacer le mouvement du skieur par le mouvement de son centre d'inertie.        1)la piste verglacé on peut alors supposer les frottements négligeable calculer la vitesse du skieur en B et en C 2) la piste est recouverte de neige la force de frottement est toujours tangent a la trajectoire et a une intensité constante f a) exprimer vA et vB en fonction de m,r,f et L mon problème est la première question j'ai mis vB=?(2gh) mon problème est h comment le déterminé alors qu'on m'a donné aucun angle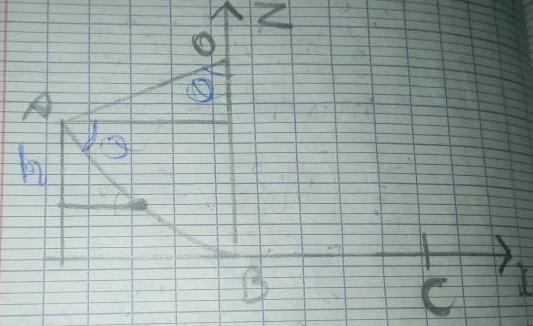

Vitesse du skieur

***Image recadrée***

Posté par
diracre : Vitesse du skieur 13-12-19 à 13:21

Hello

La trajectoire entre A et B est un arc de cercle dont la longueur est 1/6 de la circonférence

Posté par
modou15re : Vitesse du skieur 13-12-19 à 13:46

Je sais ça mais on m'a pas donné d'angle pour pouvoir utiliser relation trigonométrie

Posté par
modou15re : Vitesse du skieur 13-12-19 à 13:50

Je crois avoir compris donc h=AB(cos0-cos0/2) avec AB=10/6 j'ai trouvé 4,1m/s pour la vitesse VB est ce exact

Posté par
diracre : Vitesse du skieur 13-12-19 à 14:29

Citation :
Je sais ça mais on m'a pas donné d'angle pour pouvoir utiliser relation trigonométrie


Tu sais, tu sais ... mais:

t'es tu posé la question d'au venait cette unité d'angle bizarre que le radian?

La mesure de l'angle en radian donne la longueur de l'arc de cercle intercepté par cet angle sur le cercle trigonométrique (cercle de rayon 1)

Donc un arc qui fait 1/6 de la circonférence correspond à un angle égal à:
2 x 1/6, soit /3

Donc hA - hB = R(1-cos/3)

Posté par
gbm Webmasterre : Vitesse du skieur 14-12-19 à 10:15

Bonjour à vous deux,

@modou15 : prière de bien cadrer et de bien orienter les images postées

Posté par
modou15re : Vitesse du skieur 14-12-19 à 10:25

Oui d'accord je suis désolée

Posté par
modou15re : Vitesse du skieur 14-12-19 à 10:27

Mais j'aimerais que vous m'expliquiez pourquoi ha=R

Posté par
diracre : Vitesse du skieur 14-12-19 à 13:08

Hello

Citation :
la partie AB représente un sixième de son circonférence de rayon r=10m


Alors  \overset{\frown}{AB} = \frac{1}{6}2\pi r

Et donc pour reprendre ton schéma:

\widehat{AOB} = \frac{\pi}{3}

Et donc si OB = R et si on appelle H la projection de A sur (OB)

OH = Rcos\frac{\pi}{3}

Et donc h_A - h_B = R(1 -cos\frac{\pi}{3})

Citation :
Mais j'aimerais que vous m'expliquiez pourquoi ha=R


Du coup je ne sais pas ce que tu désignes par ha

Posté par
modou15re : Vitesse du skieur 14-12-19 à 14:08

En fait ha est le p

Posté par
modou15re : Vitesse du skieur 14-12-19 à 14:20

Je veux dire ha est le projeté de A sur OB je crois avoir compris votre raisonnement est utilisant les relations trigonométrie on peut calculer h=R-Rcosπ/3 pour la vitesse vA=(2gR(1-cosπ/3))=10m/s vA=vB=10m/s et pour la deuxième question exprimer vB et vA en fonction de m,g,r et L j'ai mis vB-vA=√(2ghR(1-cosπ/3)-f×Lcos angle(f,L) comment trouver l'angle formé par f,L

Posté par
diracre : Vitesse du skieur 14-12-19 à 15:56

hum hum ... on sent que tu sens le truc, mais mon conseil serait (si je peux me permettre) d'être précis(e).

L'exercice porte sur le Théorème de l'énergie mécanique:

"Dans un référentiel galiléen, pour un corps ponctuel de masse m constante parcourant un chemin reliant un point A à un point C, la variation d'énergie mécanique est égale à la somme des travaux des forces non conservatives  qui s'exercent sur corps"

1) Dans ce premier cas pas de frottements

\Delta E_{m,A\rightarrow C} = \Delta E_{m,A\rightarrow B} + \Delta E_{m,B\rightarrow C}

\Delta E_{m,A\rightarrow B} = \Delta E_{c,A\rightarrow B} + \Delta E_{p,A\rightarrow B} = \frac{1}{2}m(v_B^2 -v_A^2) + mg(h_B-h_A) =0

car pas de frottements entre A et B

Donc comme v_A = 0, et comme  tu l'as exprimé v_B = \sqrt{2gh_A} = \sqrt{2gR(1-cos\frac{\pi}{3})}

Par ailleurs

\Delta E_{m,B\rightarrow C} = \Delta E_{c,B\rightarrow C} + \Delta E_{p,B\rightarrow C} = \frac{1}{2}m(v_C^2 -v_B^2) + mg(h_C-h_B) =0

car pas de frottements entre B et C.

Comme h_C = h_B, on a bien sûr v_C = v_B

Donc v_C = \sqrt{2gR(1-cos\frac{\pi}{3})}

2/ Dans ce 2nd cas on a un frottement \vec{f} dont l'intensité f est constante, la direction tangente à la trajectoire et le sens opposé au mouvement

\Delta E_{m,A\rightarrow B} = \Delta E_{c,A\rightarrow B} + \Delta E_{p,A\rightarrow B} = \frac{1}{2}m(v_B^2 -v_A^2) + mg(h_B-h_A) =W_{\vec{f},A\rightarrow B}

v_A = 0
h_B = 0
h_A = R(1-cos\frac{\pi}{3})

W_{\vec{f},A\rightarrow B} = -R.\widehat{AOB}.f (la force étant toujours tangente, donc W_{\vec{f},A\rightarrow B} = -\frac{\pi fR}{3}

\Delta E_{m,B\rightarrow C} = \Delta E_{c,B\rightarrow C} + \Delta E_{p,B\rightarrow C} = \frac{1}{2}m(v_C^2 -v_B^2) + mg(h_C-h_B) =W_{\vec{f},B\rightarrow C}

h_B = h_C = 0

W_{\vec{f},B\rightarrow C} =-BC.f

Donc

\frac{1}{2}mv_c^2 -mgR(1-cos\frac{\pi}{3}) = -f(R\frac{\pi}{3}+BC)  

Je te laisse terminer? bien sur selon l'intensité de f on peut trouver l'expression d'un carré de la vitesse qui serait négatif. Cela signifierait simplement que le skieur s'arrêterait avant d'arriver en C


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !