Inscription / Connexion Nouveau Sujet
Vitesse d'un solide
Joyeux Noël à vous .
Veuillez m'aider s'il vous plaît.
Un enfant tire son jouet de masse 0,5 kg à l'aide d'une corde sur un plan horizontal .
La tension de la corde vaut 2N et les forces de frottement sont négligées . (l'angle entre le jouet et le plan horizontal est de 30°).
Déterminer la vitesse du jouet lorsqu'il a parcouru 5m
Merci d'avance .
Bonjour,
La méthode à suivre est classique:
a) Définir le système étudié, le référentiel et le repère.
b) Rechercher et caractériser les forces extérieures qui s'exercent sur le système étudié.
c)Faire un schéma soigné représentant le système étudié, le repère choisi et les forces extérieures.
d) Appliquer la 2e loi ne Newton.
e) Projeter la relation vectorielle obtenue : En déduire la valeur de l'accélération du système étudié.
f) Connaissant l'accélération et la distance parcourue, répondre à la question posée.
Salut
a)le système étudié est : le jouet de l'enfant ; le référentiel galiléen .
b) les forces extérieures qui s'exercent sur le système étudié sont : le poids du jouet , la réaction du support , la tension du fil .
Leurs caractéristiques sont :
-Poids : centre d'inertie comme point d'application ; direction verticale ; sens du haut vers le bas ;intensité de P≈5N
- Réaction du support : point d'application : le point de contact entre le solide et le support ; direction : verticale ; sens : du bas vers le haut ; intensité = celui du poids .
- la tension du fil : point d'application : contact entre le fil et le solide ; direction : (je ne sais pas comment dire ) ; sens : celui du mouvement ; valeur :T=2N.
c) (voir figure comment faire pour que les vecteurs apparaissent ?)
Pour le reste je n'y arrive pas.
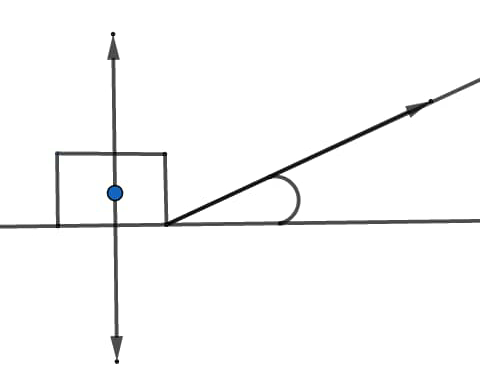
Tes réponses sont, pour la plupart, exactes.
Seule erreur notable, mais sans conséquence pour la résolution de l'exercice : L'intensité de la réaction n'est pas égale à celle du poids.
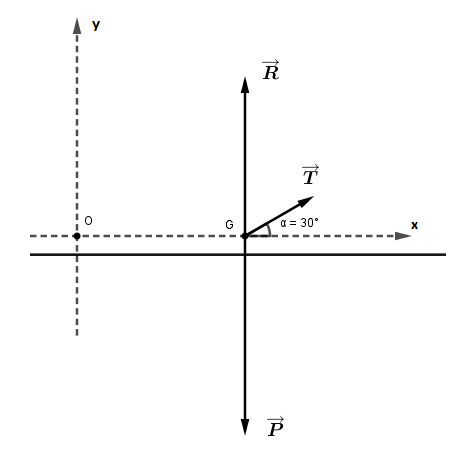
On peut considérer que les 3 forces sont appliquées au centre de gravité " G " du jouet.
Sur le schéma ci-dessous je fais apparaître ( tu ne l'as pas fait sur le tien) le repère Ox,Oy sur lequel se feront les projections.
Il te faut maintenant écrire la relation vectorielle obéissant à la 2ème loi de Newton, puis projeter cette relation sur les axes du repère.
La projection sur l'axe Ox sera suffisante pour trouver la valeur de l'accélération, mais il vaut mieux faire les deux projections.
Merci .
L'accélération subie par ce corps dans un référentiel galiléen est proportionnelle à la résultante des forces qu'il subit, et inversement proportionnelle à sa masse m.
Du coup
où :
correspond à l'accélération du centre d'inertie G du jouet .
Mon seul souci à présent est comment calculer R ?
Tu n'as pas besoin de calculer R pour répondre à la question posée.
Tu en as terminé avec les quatre premières étapes décrites dans mon post du 28-12-19 à 15:19
L'étape suivante consiste à projeter la relation :
sur les axes Ox et Oy
Tu vas ainsi obtenir deux relations algébriques.
Une de ces deux relations te permettra de trouver la valeur de " a "
L'autre te permettrait (si on te le demandait) de trouver la valeur de " R "
Les coordonnées de P ; R et T sont :
(0;-P)
(0;R)
(sin30° ; cos30°)
Voilà j'ai les coordonnées mais je ne sais pas comment faire pour trouver les deux relations algébrique .
Disons plutôt :
Les deux relations cherchées sont :
Sur Ox : 0 + 0 + T*cos(
) = m*a
Sur Oy : -P + R + T*sin() = 0
OK
Pour trouver a il serait plus judicieux de choisir sur Ox:Tcos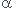
=ma
==> a=}{m}
\\ " alt="\dfrac{Tcos
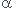}{m}
\\ " class="tex" />.
AN: T=2N , 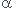=30° ;cos(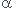)=0,86 ; m=0,5kg
a==3,44m/s
Comment faire pour trouver la vitesse du jouet lorsqu'il parcourt 5m ?
Quelle est la technique pour ne pas se tromper à la détermination des coordonnées ?
Bonne nuit .
a = T * cos() / m = 2 * cos(30°) / 0,5 = 3,46 m/s² (et non m/s)
L'accélération est constante, le mouvement est rectiligne uniformément varié d'accélération a = 3,46 m/s² , La vitesse initiale est (probablement) nulle, la distance parcourue est de 5m
Les lois du mouvement est rectiligne uniformément varié permettent de répondre à la question posée.
La seule technique qui me semble efficace est d'apprendre la définition d'un sinus et d'un cosinus et d'appliquer ces définitions.
Avec :
x0 : la position initiale du jouet
V0: la vitesse initiale
a0: l'accélération constante appliquée au jouet.
On a :
De ceci on peut déduire une relation entre l'accélération , la variation de vitesse et le chemin parcouru (x-x0):
V²=V0²+2a0(x-x0).
Donc a0=3,46m/s²
Comment trouver x ;x0 ; V0 ?
x-x0 = L ( C'est la distance parcourue )
V0 = 0 ( Enfin, on le suppose car l'énoncé ne dit rien à ce sujet )
Annuler
connectez vous