Inscription / Connexion Nouveau Sujet
Vers le bac , Energie cinétique mécanique et de pesenteur
Bonjour,
J'ai un devoir à rendre et je bloque un peu quelqu'un pourrait m 'expliquer m'aider sil vous plaît ?
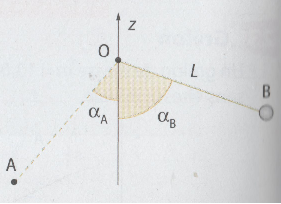
Considérons le pendule du professeur Tournesol des albums de tintin. On l'incline d'un angle αA par rapport à la verticale et on le lance à la vitesse VA =1,0m/s. Il arrive en B avec une vitesse nulle.
Données :
Longueur du pendule: L=20cm ; αA =30°
Les frottements sont négligeables.
Au point O, EPP(O) = 0J.
1) a. Déterminer l'expression des altitudes en A et B, ZA et ZB, en fonction de L et respectivement αA et αB.
b. En déduire les expressions des énergies potentielles de pesanteur du pendule en A et B.
2) a. Donner les expressions des énergies mécaniques du pendule en A et B.
b. En déduire l'expression de l'angle maximum αB atteint par le pendule. Calculer sa valeur.
Bonjour,
Que valent ZA et ZB les cotes des points A et B ?
Attention, la figure indique que l'axe des cotes (l'axe OZ) est orienté vers le haut.
Je suppose que l'origine sur cet axe est à prendre au point O (qui sera aussi le niveau de l'origine des calculs de l'énergie potentielle de pesanteur).
Merci d'avoir répondu
J'en suis à ça :
pour la 1)
On a L=20 cm
cos(
a)=adj/hyp ; cos(a)=za/L donc
za=20-[cos(30)*20]
cos(b)=adj/hyp ; cos(b)=zb/L donc
zb=20-[cos(b)*20]
b- On sait que Epp=m*g*z
donc Eppa=m*g*za=m*9.8*[cos(30)*20]
Eppb=m*g*z=m*9.8*[cos(b)*20]
2)
On sait que Em=Ec+Epp
Donc Ema=1/2*m*(1.0)²+m*9.8*[cos(30)*20]=1/2*m+169.74*m=m(169.74+1/2)
On sdait que la vitesse en B est nulle donc Vb=0
Emb=1/2*m*v²+m*9.8*cos(b*20=9.8*cos(b)*20
b-
Emb=9.8*cos(b)*20
donc cos(b)=9.8/20=0.49
b=60.65°
Mais je ne pense pas que c'est bon
Tu n'as pas bien lu l'énoncé (ni ma réponse).
Au point O, EPP(O) = 0 J
________________
On ne te demande un calcul qu'à la fin. Pour tout le reste on te demande seulement les expressions (pas les valeurs).
L'axe Oz est orienté vers le haut. O est l'origine des altitudes.
Par exemple ZA sera donc négatif ainsi que l'énergie potentielle de pesanteur en A
_ _ _ _ _ _
Question 1a)
Z = - L.cos(
)
donc
ZA = - L.cos(
A)
ZB = - L.cos(
B)
Question 1b)
Epp = m.g.Z
donc
Epp,A = m.g.ZA = - m.g.L.cos(
A)
Epp,B = m.g.ZB = - m.g.L.cos(
B)
Question 2a)
Em = Epp + Ec = Epp + (1/2).m.v2
donc
Em,A = Epp,A + Ec,A = Epp,A + (1/2).m.vA2 = - m.g.L.cos(
A) + (1/2).m.vA2
Em,B = Epp,B + Ec,B = Epp,B + (1/2).m.vB2 = - m.g.L.cos(
B)
puisque vB = 0 m.s-1
Question 2b)
En l'absence de frottements, l'énergie mécanique est constante et donc Em,A = Em,B
On en déduit l'angle
B
Application numérique :
(tu as aussi oublié de convertir la valeur de la longueur L en mètre...)
Sauf erreur, vérifie...
Merci pour la correction et votre aide car j'ai fais beaucoup de bêtises!
Si j avais lu votre réponse juste que le professeur nous avez pas préciser que si l'axe est orientée vers le haut que cela signifierait que Epp serait négatif (donc j'ai appris quelque chose de plus merci).!!!
La question est bête mais je voudrait savoir si il existe des axes orientées vers le bas(j'ai jamais vu en cours donc voilà ) ?
Et je trouve que 
54°
Vous pouvez m 'expliquez sil vous plaît comment vous avez fait pour trouvez la formule de la question 2 .J 'ai travaillé dessus et j'arrive toujours pas à comprendre comment vous avez trouvez cette formule
Em,A = Em,B
donc
- m.g.L.cos(A) + (1/2).m.vA2 = - m.g.L.cos(B)
Il est facile d'en déduire cos(B)
puis
B = cos-1[cos(B)]
Je sais j 'ai fait ça mais après j 'arrive pas comme votre formule:
- m.g.L.cos(A) + (1/2).m.vA2 = - m.g.L.cos(B)
Je me retrouve avec
- m.g.L.cos(A) + (1/2).m.vA2/- m.g.L=cos(B)
-cos(A)+vA2/2*(m*g*l)
Merci même si je suis pas arrivée à trouvée la même formule que vous
Annuler
connectez vous