Bonjour,

Quelques pistes:

G est le milieu des points G₁ et G₂

La vitesse v de G se décompose en 2 parties égales sur l'axe G₁G₂ et sur l'axe perpendiculaire car elle fait un angle de 45° avec l'axe G₁G₂

Ensuite il faut certainement appliquer la loi de composition des vitesses pour le point G à partir de celles des points G₁ et G₂ suivant les 2 axes.

Voir dans le cours s'il n' ya pas un exemple ou un exercice ressemblant à cela.

A+

Re-bonjour,

Peut-être une autre piste avec l'énergie cinétique en remarquant que G₁ et G₂ ont la même masse m puisque G est au milieu de G₁G₂, ce qui signifie que G a une masse 2m.

Il faudrait alors retrouver la loi de composition des énergies cinétiques

A+

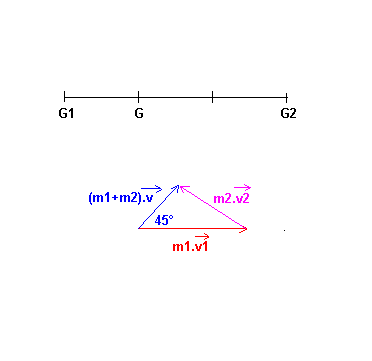
m1.|v1| = 0,2 * 0,8 = 0,16 kgm/s

(m1+m2).|v| = (0,2 + 0,1) * 0,2*V2 = 0,06 * V2 kgm/s

Alkashi dans le triangle des quantités de mouvement. :

(m2.|v2|)² = (m1.|v1|)² + ((m1+m2).|v|)² - 2 * m1.|v1| * (m1+m2).|v| * cos(45°)

(m2.|v2|)²  = 0,16² + (0,06 * V2)² - 2 * 0,16 * 0,06 * V2 * (1/V2)

(m2.|v2|)²  = 0,16² + 0,0072 - 0,0192

(m2.|v2|)² = 0,0136

m2.|v2| = 0,1166 kgm/s

|v2| = 0,1166/0,1 = 1,166 m/s

|v2| = 116,6 cm/s
-----
Au lieu d'utiliser Alkashi, on peut évidemment aussi projeter les vecteurs sur 2 axes et ...


Sauf distraction.  

Un très grand merci à J-P. Je pense que je n'aurai pas cherché ds cette voie...que pourtant je connaissais par ailleurs...

Ton explication est parfaite ; j'ai seulement mis qqs minutes à la comprendre car pdt un moment je lisais V2 comme v2 alors que c'était 2.

M

J'avais pas fini mon message qui s'est posté tt seul !!!

Donc Merci bcp pr ton explivcation lumineuse (que j'imprime et conserve) e puis pas de pb pr le V2, après tt qd 'est le vecteur tu écris bien v2 et non pas V2.

Bon dimanche, à bientôt

Philippe..

Bonsoir,

Autant pour moi, je suis allé trop vite sur la position de G (sans avoir vu que les masses étaient données)!

La compréhension que V1 est parallèle à l'axe G1G2 m'a totalement échappé car pour moi il s'agissait de la projection de V1 sur l'axe G1G2.

Comme quoi, précipitation et incompréhension ne mènent à rien de bon.

Salut Revelli,

Juste pour info, ce lien que j'aime beaucoup :

Revelli,

merci qd même pr ton aide surtt un diamnche matin ; j'avais bien vu que tu n'avais pas tt intégré du pb tel que je l'avais exposé, mais avec l'explication de JP qui a suivi je m'en suis très bien sorti.

Encore merci à vous deux.

salut,j'espere que vous allez bien!
  j'ai un p'tit probleme pour determiner l'angle formés entre ces paires de vecteurs:

1)a1=3i-j et b1=2i+2j

2)a2=-i+4j et b2=2i+j+2k

3)a3=3i+j+3k et -2j+3k


    deja,grand merci pour votre aide!
          
                                    dia

bonsoir dia,

Utilise le produit scalaire sous forme géométrique et analytique :

u.v = ||u|| ||v|| cos(u; v)
u.v = xx' + yy' + zz'

...

Rebonsoir,

J'avoue que les 2 expressions s'appliquent bien:

- au temps pour moi, car comme le note Philibert, c'était au saut du lit un dimanche matin,

- autant pour moi, car il y a un retour qualitatif (la honte) dont le quantitatif ne fait qu'aggraver l'effet.

Mais, ce que j'aime par dessus tout, c'est que je continue à apprendre à chaque instant et qu'on arrive plus que très souvent à retirer du positif de ses erreurs (alors que la réussite  n'apporte pas la même solidité à la compréhension car on peut par exemple avoir trouvé par hasard).

Mais arrêtons là, l'épreuve de philo du bac général était pour lundi dernier!

Bonne fin de week end à tous.