Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Une seule question d'un exercice sur L'Em et les forces

Posté par
mousse6994 16-03-11 à 18:25

Bonjour,

Je sais qu'il est inapproprié d'ouvrir un nouveau topic sur un sujet déjà posté plusieurs fois, mais voilà je voulais que qqun voit mon message et surtout ne pas être en fouillis avec ce qu'ont dit d'autres personnes. Voilà mon énoncé:

Une cabine de funiculaire, de masse m=3,2 t, se déplace le long d'une pente inclinée de 45° par rapport au plan horizontale. Elle est tractée par un câble tendu par l'action d'un moteur électrique.

1° Quelle est la nature du mouvement de la cabine ?

2° La phase de démarrage a lieu sur une longueur d=10 m ; la cabine atteint alors la vitesse de 3,0 m/s.
Calculer la variation :
a) d'énergie cinétique
b) d'énergie potentielle
c) d'énergie mécanique de la cabine

3° Sur une longueur L=130 m, la cabine a un mouvement rectiligne et uniforme avec la vitesse acquise dans la phase de démarrage. Les frottements de la cabine sur la voie sont modélisables par une force de force f=k.P, avec P le poids de la cabine et k=0.060.
a) Faire l'inventaire des forces agissant sur la cabine
b) Quelle relation ces forces vérifient-elles ?
c) Déterminer la force de traction exercée par le câble.
d) Calculer le travail fourni par cette force au cours du déplacement.
e) Calculer la variation de l'énergie mécanique de la cabine. La comparer au travail fourni par la traction du câble et conclure.

4° Pendant la phase de ralentissement jusqu'à l'arrêt, la traction du câble est réduite à la valeur T'= 22.6 kN.
Les autres forces ne sont pas modifiées.
a) Faire l'inventaire des forces agissant sur la cabine.
b) Calculer la valeur de F, résultante tangentielle de l'ensemble des forces appliquées à la cabine, et donner son sens.
c) Exprimer le travail fourni par cette résultante en fonction de la distance d'arrêt d.
d) Énoncer le théorème de l'énergie cinétique. Calculer la distance d'arrêt de la cabine.



Alors j'ai réussi à tout faire sauf la question 4)b en fait je n'en suis pas sûre. Je mets d'abord ce que j'ai trouvé avant, puisqu'il le faut je suppose.

1) Mouvement d'abord rectiligne et accéléré, puis uniforme, puis décéléré selon les phases.
2)a deltaEc : 14400 J
  b delta Epp : 226 274,17 J
  c.delta Em : somme des deux précédents: 240 674,17 J

3)a. Forces: P, T, Rn, f
  b. D'après principe d'inertie: SommeF: P+T+RN+f = 0
  c.J'ai fait un repère:
grâce aux cosinus, aux axes Ox et Oy j'ai trouvé

T= 24 547,417
Rn= 22627,417

d. W(T) = TLcos(45)= 2 941 564,21 J

e.delta Ec n'a pas changé
delta Epp = 2 941 564,21 J
delta Em= 2 955 964,21 J

W(T) est quasi aussi élevé que L'energie mécanique car il soulève une masse importante sur une pente raide, c'est la force qui travaille le plus, logique.

4) a Mêmes forces mais T remplacé par T'
   b. Mon problème:

Somme F = P+T'+Rn+f

Je crois qu'on a la droit d'enlever les vecteurs mais dans ce cas il faudrait changer les signes de certaines forces... Je ne sais plus... ?

Quelqu'un peut il m'aider ? J'en serai très reconnaissante !

Merci d'avance (;

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 16-03-11 à 20:39

Bonsoir,
1 ==> OK
2 ==> OK   (avec g = 10 m.s-2)
3 ==> je ne trouve pas tout à fait ça pour T (tu as pris g = ? )
      OK pour R (qu'on ne demande pas d'ailleurs)
3d ==> WT = T L  avec L = 130 m
3e ==> plus tard

Dans la 4b, c'est la même chose que dans 3b.
Il faut projeter les forces sur deux axes perpendiculaires, un parallèle au plan incliné et l'autre perpendiculaire au plan incliné.
Sur l'axe (orienté vers le haut) parallèle au plan incliné, on a :
3$T^'\,-\,P\,sin\alpha\,-\,f
Sur l'axe perpendiculaire au plan incliné (orienté vers le haut), on a :
3$R_N\,-\,P\,cos\alpha

Posté par
mousse6994Rép: 17-03-11 à 18:31

Bonjour,

Merci bcp !

Alors J'ai tjs pris g=10

T= Px+f ? Enfin c'est ce que j'ai trouvé grâce à l'axe des Ox.

Et dans Wt c'est cos 0 c'est ce que j'avais mis, je me suis trompée en tapant =/

Et pour la question-problème je n'avais pas du tout pensé à faire ça !! Je vais le faire alors merci bcp ! Je dirai ce que j'ai trouvé !

(; Cdt

Posté par
mousse6994Rép: 17-03-11 à 18:48

Mais il y a qqpoints que je ne comprends pas:

Pq deux plans ? Je croyais que l'"ordre" dans lequel on mettait le plan importait peu...

Comment êtes vous parvenus à 3$T^'\,-\,P\,sin\alpha\,-\,f ?

Et est ce que c'est Somme F ? Pcq pour le nouvel axe parallèle au plan j'ai:

Rn=Px
Py+f=T

Mais pourtant, l'angle ne change pas donc, P reste pareil ainsi que ces composantes px et Py, f aussi... ce qui ne devrait pas influer sur T pourtant d'après l'énoncé,  cette force baisse d'intensité (j'ai compris, c'est un moteur électrique...)

Bref.... Je ne vois pas comment vous êtes arrivé aux 2 calculs... ?

Merci encore pour votre aide précieuse

Posté par
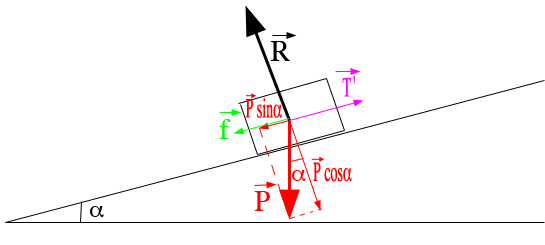
Marc35re : Une seule question d'un exercice sur L'Em et les forces 17-03-11 à 19:03

Il faut faire un schéma... que je vais faire mais il me faut un peu de temps...

Posté par
mousse6994rép: 17-03-11 à 20:24

Dsl... En fait, je l'ai fait, enfin les 2 axes, et au tout début de l'exercice, j'ai fait le schéma de la pente avec la cabine, et les forces... J'ai trouvé pour l'axe parallalèle T en y Rn en x, f en -y et P entre f et -x.

Avec 45 degrés entre P et f.

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 17-03-11 à 22:18

Sur le schéma, on voit que, sur l'axe y orienté vers le haut :
R - P cos = 0
et sur l'axe x (parallèle au plan incliné et orienté vers le haut) :
T' - P sin - f

Une seule question d\'un exercice sur L\'Em et les forces

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 17-03-11 à 22:20

Sur le schéma, l'angle ne fait pas 45°...

Posté par
mousse6994Rép: 18-03-11 à 12:46

Ah bon ? alpha ne fait pas 45° ? Pourtant c'est l'angle de la pente alors je croyais qu'on pouvait le projeter Pour P et f, ou P et l'axe des abscisses... Quel autre angle pourrait-on avoir ?

Pcq c'est cette projection que j'avais depuis le début, même que j'avais trouvé une valeur de T différente de la vôtre... Sans doute pcq on a pas le même angle ^^'

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 18-03-11 à 19:21

est égal à 45° dans l'exercice.
Ce que je voulais dire (j'aurais dû m'abstenir) est que le schéma n'est pas à l'échelle (sur le schéma, l'angle ne fait pas 45°). J'ai pris un ancien schéma plutôt que d'en faire un nouveau..

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 18-03-11 à 19:22

Mais cela ne change rien pour le principe de projection des forces sur les axes.

Posté par
mousse6994Rép: 18-03-11 à 19:30

Ah oui pas de souci... J'avais juste pas compris que vous parliez de ce schéma, et pas de l'exercice, oui ça importe peu. "Mais cela ne change rien pour le principe de projection des forces sur les axes." Je vois que vous voulez visiblement m'aider et j'en suis très contente !! Mais il me faudrait un peu plus de... développement ? Pour que je comprenne où je fais erreur en fait. Pcq depuis le début que vous me dites que j'ai tord pour T, vous ne me dites pas pourquoi


"Pcq c'est cette projection que j'avais depuis le début, même que j'avais trouvé une valeur de T différente de la vôtre... Sans doute pcq on a pas le même angle ^^' " Quand je dis cela, en fait ce n'est plus d'actualité, mais nous avons toujours des T qui diffèrent...
Ah moins en fait que depuis le début, mon T est différent du vôtre à cause de la valeur de g ? Comme je l'ai dit j'ai pris 10. Vous aussi ?

Et du coup je n'ai en même temps pas compris SommeF... Je suis désolée, je ne suis pas nulle en physique, c'est juste que pour le coup, calculer la résultante des forces de cette façon... On ne l'a jamais fait !

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 18-03-11 à 23:59

Non, pour T, je suis d'accord. Mon 1er résultat était peu différent mais, en fait, j'ai fait une erreur.
Pour les forces, sur un plan incliné, il faut toujours décomposer sur deux axes : un axe x parallèle au plan incliné et un axe y perpendiculaire au plan incliné.
Dans la question 3, la somme des forces est nulle parce que la vitesse est constante.
Dans la question 4, la vitesse n'est pas constante donc la somme des forces n'est pas nulle.
Il faut donc projeter les forces sur les axes. Cela donne quelque chose qui ressemble au schéma.
Donc, pour répondre à 4a, on a T', P, R, f.
Pour 4b :
"la valeur de F, résultante tangentielle de l'ensemble des forces appliquées à la cabine"
Pourquoi "tangentielle" ? Le moins qu'on puisse dire est que la question est mal posée !
Il est probable qu'il s'agisse de la force résultante parallèle au plan incliné.
Donc :  F\,=\,T^'\,-\,P\,sin\alpha\,-\,f   (sur l'axe x)
Sur l'axe y, la somme des forces est nulle (v_y\,=\,0, la vitesse est parallèle au plan incliné) ==> R\,-\,P\,cos\alpha\,=\,0
Pour 4c :
Le travail de F sur la distance d est W = F d
Pour 4d :
\Delta E_c\,=\,W
0\,-\,\frac{1}{2}mv^2\,=\,F\,d
avec v = 3 m.s-1

Posté par
mousse6994Rép: 19-03-11 à 11:16

D'accord !! Tout est maintenant bien plus clair. En fait j'ai fait une erreur depuis longtemps, vraiment très idiote de ma part, en fait quand vous disiez deux axes, je comprenais deux repères !!!

Sinon, maintenant je comprends parfaitement pourquoi vous faites UN repère pour trouver F. Enfin,... Comme je l'ai déjà dit je ne l'avais jamais calculé ainsi, mais je comprends qu'on le puisse.

Et les questions après la  4)b. j'avais réussi mais avec une mauvaise valeur de F...

Je vais la calculer, avec ce que vous m'avez donné. Et vous me direz si c'est le résultat que vous trouvez ?

Merci infiniment !  

Posté par
mousse6994Rép: 19-03-11 à 11:27

D'ailleurs, P x sin(alpha) en fait, on peut l'écrire P x cos(alpha) je viens de voir que c'est égal. Tant mieux, moins d'erreurs !

Posté par
mousse6994Rép: 19-03-11 à 11:35

Alors voilà ce que j'ai trouvé:

F = -1947

Je me suis dit que c'était impossible qu'une résultante soit négative, alors j'ai plutôt fait:

F= Psin(45) + f - T
= 1947

Ai-je le droit de faire cela ?

Ca me semble être un bon chiffre personnellement, mieux que 79 147,417 que j'avais trouvé avant tout au début en tout cas...

Posté par
mousse6994Rép: 19-03-11 à 11:43

Enfin, j'ai calculé d la distance d'arrêt. Je passe les calculs puisqu'on les connait tous (=

d= 7,39 m ?

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-03-11 à 13:10

F = -1247 N, c'est correct...
Cela indique simplement que la norme (valeur) de la force est 1947 N et qu'elle est orientée dans le sens négatif de l'axe c'est-à-dire vers le bas du plan incliné (cela fait partie de la question d'ailleurs).
Autrement dit, la cabine est freinée.
Le travail de cette force F est forcément négatif parce que la force est opposée au déplacement. Je rappelle que le travail est un produit scalaire  W\,=\,\vec{F}\,.\,\vec{d}\,=\,||\vec{F}||\,.\,||\vec{d}||\,.\,cos(\vec{F},\vec{d})  et on a  cos(\vec{F}\,,\,\vec{d})\,=\,cos(\pi)\,=\,-1.
Donc, pour le travail de la force, il est préférable de mettre  W\,=\,-\|F|\,d pour bien montrer que le travail est négatif.
Ensuite :
\Delta E_c\,=\,W
0\,-\,\frac{1}{2}mv^2\,=\,-\,F\,d
On part d'une vitesse de 3 m.s-1 pour arriver à une vitesse nulle (arrêt).
3$\frac{1}{2}mv^2\,=\,F\,d\,\Rightarrow\,d\,=\,\frac{\frac{1}{2}mv^2}{F}
Et, effectivement, on trouve d = 7,39 m  (ou 7,4 m).

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-03-11 à 13:11

Erreur ==> "F = -1247 N, c'est correct..." ==> F = -1947 N, c'est correct...

Posté par
mousse6994Rép: 19-03-11 à 14:08

Vraiment ? Mais alors quand on calcule le travail, ca nous donne

W(F)= Fxd x cos(180)
    = 1947d

Or le travail doit être négatif pour deux raisons:

la première, qui répond à la physique, est que le travail va vers l'arrière comme deltav donc il est un travail résistant

la seconde, qui répond à la logique, est que pour que la distance soit positive, obligatoirement, le trvail DOIT être négative, pour que diviser négatif sur négatif donne positif ?

Je fais fausse route ?

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-03-11 à 15:02

Oui, tu fais fausse route...
On trouve F négatif parce qu'on a projeté les forces sur des axes orientés. Le signe - est mathématique. Il indique simplement que F est orientée dans le sens négatif de l'axe.
Physiquement, F est une force de 1947 N parallèle au plan incliné et dirigée vers le bas du plan incliné. Elle est opposée au mouvement donc le travail est négatif (travail résistant).
Quand on écrit le produit scalaire W\,=\,\vec{F}\,.\,\vec{d}\,=\,||\vec{F}||\,.\,||\vec{d}||\,.\,cos(\vec{F}\,,\,\vec{d}), ||\vec{F}||  et  ||\vec{d}||  sont des longueurs donc positives. Le signe - vient du fait que les vecteurs \vec{F}  et  \vec{d}  ont des sens opposés c'est-à-dire cos(\vec{F}\,,\,\vec{d})\,=\,cos(\pi)\,=\,-1.

Posté par
mousse6994Rép: 19-03-11 à 23:49

Oups!! Je n'avais pas vu votre message avant celui "erreur..." dans lequel vous expliquez déjà cela... Dsl que vous ayez dû répéter la même chose... Si j'avais mieux lu... =/

Ah d'accord je ne savais pas que l'on prenait les valeurs absolues de F et l'angle. Par contre je savais que cos (180) fait -1 puisque c'est ce que j'ai écrit dans mon calcul du travail. Donc en gros j'ai juste. F est égal à 1947. Le travail est négatif. J'avais faux pour le calcul de F.

Merci pour tout en tout cas !!!

Bonne continuation, et continuez d'aider les gens dans le besoin (;

Cdt

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 14:34

Je fais actuellement le même exercice, je ne comprends pas pourquoi le travail de la tension (question 3D) est positif ? Car sur mon schéma l'angle entre L et T vaut 180° donc mon cos devrait me donner -1.... HELP.
Merci

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 16:30

Parce que T et le déplacement sont dans le même sens (le funiculaire monte la pente).
Donc l'angle vaut 0°, pas 180°...

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 16:32

Ah mais oui il monte ! suis-je bête! Merci Marc Mais dans la dernière phase il descend donc le cosinus est bien égal à -1 ?

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 16:54

Non, dans la dernière phase, il ralentit pour s'arrêter mais il monte toujours...
1ère phase : mouvement accéléré pour atteindre 3 m/s
2ème phase : mouvement uniforme
3ème phase : mouvement décéléré puis arrêt à la fin

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 16:56

Et pourquoi le cosinus vaut -1 dans la dernière phase alors ?

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 16:58

Non, le cosinus vaut 1 dans la dernière phase aussi, enfin pour T...

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 17:01

D'accord merci Marc, je vois. Et pour determiner la variaion d'énergie mécanique de la cabine dans la première phase que dois-je faire ? C'est la seule question que je n'arrive pas à faire... En tout cas merci beaucoup de bien vouloir vous replonger dans cet exercice!

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 17:25

On a : Em = Ec + Ep
Donc : Em = Ec + Ep
Comme Ec et Ep ont été calculés en 2a et 2b, ça devrait pouvoir se faire...

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 18:22

D'accord, mais le 2a) et b) sont utilisés pour le 2c) donc je suis sensée obtenir le même résultat ?

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 19:02

Le même résultat que quoi ?

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 19:03

Que pour la question 2c) ?

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 20:09

Oups ! J'ai du mal à suivre...

Citation :
pour déterminer la variation d'énergie mécanique de la cabine dans la première phase que dois-je faire ?

La 1ère phase, c'est bien la question 2 ?...
Donc 2a, calcul de la variation d'énergie cinétique
2b, calcul de la variation d'énergie potentielle
2c, calcul de la variation d'énergie mécanique = somme des deux précédentes

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 20:13

Je demandais pour la question 3e)
e) Calculer la variation de l'énergie mécanique de la cabine. La comparer au travail fourni par la traction du câble et conclure.

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 20:30

C'est donc la deuxième phase !
La vitesse étant constante, la variation d'énergie cinétique est nulle.
Je suppose que tu as calculé la variation d'énergie potentielle.
Cela doit être quelque chose comme : Ep = mgh = 3,2.103.9,81.(130.sin45°)
Donc, pour la variation d'énergie mécanique, elle est égale à la variation d'énergie potentielle (puisque Ec=0).

Posté par
SiGiire : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 20:35

Ah mais oui, c'est parceque le mouvement est rectiligne uniforme ?
Merci Marc j'ai enfin fini mon exercice

Posté par
Marc35re : Une seule question d'un exercice sur L'Em et les forces 19-04-11 à 20:43

Oui, le mouvement étant rectiligne uniforme, la vitesse est constante donc Ec = 0


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !