Inscription / Connexion Nouveau Sujet
Un exercice qui demande du recul (Energie mécanique)
Bonjour,je coince sur un exercice de physique depuis quelque heure.
En voici l'enoncé ,
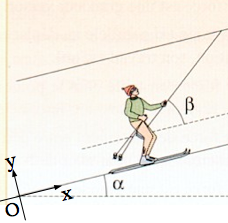
Un skieur de masse m=80kg avec son équipement est tiré par un remonte-pente.
Pendant le trajet sur une pente inclinée de 20° par rapport à l'horizontale, la valeur moyenne des forces de frottement est de 40N. La perche exerce sur le skieur une force qui fait un angle de 15° par rapport à la pente. Le skieur monte à vitesse constante dans un référentiel terrestre.
1. Représenter les forces extérieures exercées sur le skieur sans tenir compte de leurs valeurs.
2. Déterminer les coordonnées des forces extérieures en fonction du repere (o,x,y)
La question 1) en soit est simple et ne demande pas de grande connaissance.La 2) en revanche,mérite plus d'attention.Je sais éperdument qu'il faut projeter les vecteurs sur l'axe mais on m'a jamais appris à le faire.J'ai tenté en vain de comprendre,j'ai cherché plusieurs heures sur le net,je ne trouve que le corrigé sans aucune explication.Merci d'avance de m'expliquer comment réalisé cette projection de vecteurs.
Cordialement,Mistiratop
Bonjour,
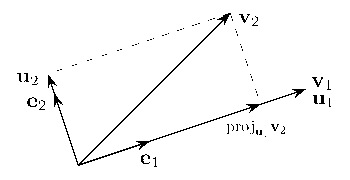
Sur l'image jointe, j'appelle l'angle entre
et
.
Si vous regardez le triangle rectangle formé par ces deux vecteurs et la ligne en pointillé sur la droite de la figure, vous avez
(à vous de compléter) ? Et donc vous en déduisez la projection de
sur l'axe porté par
.
Sur l'autre axe, la projection cherchée est la même que la longueur de la ligne pointillée sur la droite de la figure. Je reprend le même triangle rectangle que juste au dessus, et cette fois-ci, j'écris
(à vous de compléter là aussi) ? Et donc, vous avez maintenant l'autre projection.
On peut aussi faire tout ceci en passant par les produits scalaires, mais je n'aime pas, c'est moins clair et moins intuitif. Alors qu'avec les formules des sinus et cosinus dans un triangle rectangle, il suffit de faire le bon dessin et on s'en sort toujours.
Je comprends ce que vous avez mais parcontre je n'ai pas compris comment il faut faire pour determiner les coordonnées du Poids du skieur par exemple :/
Re,
Les coordonnées du poids du skieur, cela ne veut rien dire.
Parlez-vous des coordonnées su skieur ou des composantes du vecteur poids ?


