Inscription / Connexion Nouveau Sujet
un cylindre plein homogène
Bonjour
J'aurais besoin d'aide pour cet exercice :
Chapitre : énergie cinétique.
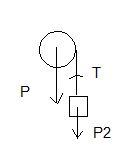
Sur un treuil assimilable à un cylindre plein homogène de masse M et de rayon R est enroulé un fil inextensible de masse négligeable. Le fil porte une masse m.
On donne m= 10kg; M=2kg; R=10cm.
1 . Calculer le moment d'inertie du treuil par rapport à son axe de révolution .
2. Le système est lâché sans vitesse initiale.
-Calculer après un parcours de h= 2 m de la masse;
-la vitesse acquise par cette masse;
- la vitesse angulaire du treuil;
- le nombre de tours effectués par le treuil
Mes réponses :
1.
J =1/2 MR^2= 2*0,1= 0,2Kg.m2
=1/2 MR^2= 2*0,1= 0,2Kg.m2
2.
Système : masse m
BFA: T; P2
<==> avec TEC
Ecf= mgh+T.h
Est-il juste ?
Merci d'avance 
Re !!!!!!
La valeur du moment d'inertie est à revoir, vous vous trompez dans l'application numérique.
Pour la seconde question, on n'a pas T = P2, sinon, ça ne démarrerait pas.
Même conseil que dans votre topic "Energie cinétique n°6", travaillez en considérant le système {cylindre, masse m} ainsi, les tensions de fil deviennent des forces intérieures. Attention le système comportant alors une partie en translation et une autre en rotation, vous aurez à prendre en compte 2 types d'énergie cinétique.
A vous.
Ok
2.
-La vitesse acquise par cette masse:
BFA: P1 et P2
<==>
1/2.mV2f+J 2= -Mgh+mgh
2= -Mgh+mgh
Or
- ( 1 / 2. mV^2i-J (omega)^2i )=0 ==>
(Omega )^2= -mV^2/2J
Remplacé par sa valeur dans l'expression ci-dessus ===>
Vf2=
Est-il correct ?
Merci d'avance 
1)
J = 1/2 * M * R² = 1/2 * 2 * (0,1²) = 0,01 kg.m²
2)
mgh = 1/2.m.v² + 1/2.J.w² (conservation de l'énergie mécanique du système treuil + masse)
mgh = 1/2.m.v² + 1/2* (1/2 * M * R²) * (v/R)²
mgh = 1/2 * m.v² + 1/4 * M.v²
4mgh = 2 * m.v² + M.v²
v² = 4mgh/(M + 2m)
v = RC[4mgh/(M + 2m)]
v = RC[4*10*10*2/(2 + 20)] = 6,0 m/s
w = v/R = 60 rad/s
d = 2 m
1 tour de treuil (périphérie) : d' = 2Pi*R = 0,2*Pi
Nombre de tours du treuil : N = d/d' = 2/(0,2.Pi) = 3,18
-----
Sauf distraction. 
Donc le poids du treuil est nul ?
Mais non, on te donne sa masse (M = 2 kg) et donc son poids n'est pas nul.
Par contre ce "poids" ne change pas d'altitude et donc pas de raison de trouver un terme Mgh dans tes relations.
On tient compte de la masse du treuil via la valeur de J ... qui influencent les résultats.
mgh = 1/2.m.v² + 1/2.J.w²
...
J'ai l'impression que tu ne comprends pas bien le pourquoi des expressions que j'ai écrites (comme celle que je viens de réécrire), c'est pourtant ce qu'il y a de plus important (bien plus que la résolution numérique qu'on fait à partir de ces relations).

J'ai l'impression que tu ne comprends pas bien le pourquoi des expressions que j'ai écrites (comme celle que je viens de réécrire), c'est pourtant ce qu'il y a de plus important (bien plus que la résolution numérique qu'on fait à partir de ces relations).

si je ne me trompe pas c'est théorème de Koening ; lorsqu'on a deux types de mouvements
non?
Donc le poids du treuil est nul ?
Comme J-P vous l'a dit, le poids du treuil n'est pas nul, c'est le travail du poids du treuil qui est nul.


