Inscription / Connexion Nouveau Sujet
Trouver une intensité
Bonjour,
J'ai besoin d'aide pour répondre a une question.
La question est de trouver l'intensité I1.
voila le schéma:
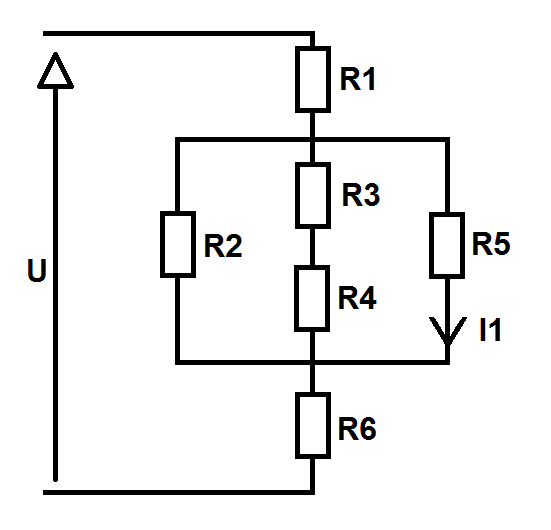
Merci d'avance
J'ai pas tout compris,
ce que j'ai compris c'est que:
R équivalente (dans la branche ou il y a R3 et R4)=(R3+R4)
R équivalente (des trois branches en dérivation)= (R2*R5*(R3+R4))/(R2+R5+(R3+R5))
donc R équivalente (pour toute les résistances)= (R1+((R2*R5*(R3+R4))/(R2+R5+(R3+R5)))+R6)
Mais j'ai pas compris comment on trouve I1, votre calcule est sans doute juste mais je ne le comprend pas
En appelant R = R2//(R3+R4)//R5, on a
Itotal=U/(R1+R+R6)
La tension V aux bornes de R vaut donc RItotal = RU/(R+R+R6)
Le courant I1 dans R5 vaut donc V/R5 = RItotal/R5=RU/(R1+R+R6)R5
Détail de calcul de R:
R=R2//(R3+R4)//R5
=R2R5(R3+R4)/[R2R5+R2(R3+R4)+(R3+R4)R5]
alors sa parait compliquer votre façon de faire, je vous propose autre chose en espérant que cela est juste
U5=R5*I1 (sa c'est ce que vous avez ecrit)
je nomme U1 le courant passant par R1 et U6 celui de R6
enfin U'celui passant dans les trois branche (U'=U2=U3/4=U5)
U=U1+U'+U6 (loi des maille)
U'=U-U1-U6
U5=U'
U5=U-U1-U6
I1=U5/R5
I1=(U-U1-U6)/R5
U=RI
U1=R1*I
U6=R6*I
U1=(U-I(R1-R6))/R5
Tu mélanges souvent les U et les I. Ex:
je nomme U1 le courant passant par R1
Les U, ce sont des tensions. Les I, des intensités (ou courants).
U1 est donc plutôt la tension aux bornes de R1 et U6 la tension aux bornes de R6.
Mais bon.
A la dernière ligne, U1 ou I1?
Sans doute I1. Mais il manque l'expression de I et, dans la parenthèse, c'est plutôt (R1+R6).
Or, l'expression de I, c'est U/(R1+R+R6) Ce qui va "compliquer" ta formule...
euh oui pardon les tensions
et la dernière ligne oui c'est I1
je sais pas après, et votre façon de faire j'ai du mal
Oui.
Mais ça t'avance à quoi?
Pour connaitre U1 et U6, il te faut le courant que j'ai appelé Itotal Non?
Par U/Rtotal en appelant Rtotal la résistance équivalente à R1, R2, ..., R6
Reste donc à calculer Rtotal 
a ben oui que je suis bête
Rtotal=R1+R6+((R2*R5*(R3+R4))/(R2+R5+(R3+R4)))
U=R*I
I=U/R
I=U/(R1+R6+((R2*R5*(R3+R4))/(R2+R5+(R3+R4))))
donc I1=(U-(U/(R1+R6+((R2*R5*(R3+R4))/(R2+R5+(R3+R4)))))(R1-R6))/R5
ah ben oui mais qu'est ce qui m'arrive
donc je récapitule:
R équivalente (dans la branche ou il y a R3 et R4)=(R3+R4)
1/R équivalente (des trois branches en dérivation)= 1/R2 + 1/(R3+R4) + 1/R5
R équivalente (des trois branches en dérivation)=[(R3+R4)R5+R2R5+R2(R3+R4)]/R2(R3+R4)R5= (R5R2+R5(R3+R4)+R2(R3+R4))/(R2*R5(R3+R4))
donc R équivalente (pour toute les résistances)= R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2*R5(R3+R4)))
U5=R5*I1
je nomme U1 la tension passant par R1 et U6 celle de R6
enfin U' celle passant dans les trois branche (U'=U2=U3/4=U5)
U=U1+U'+U6 (loi des maille)
U'=U-U1-U6
U5=U'
U5=U-U1-U6
I1=U5/R5
I1=(U-U1-U6)/R5
U=RI
U1=R1*I
U6=R6*I
I1=(U-I(R1-R6))/R5
U=R équivalente*I
R équivalente=R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2*R5(R3+R4)))
I1=(U-(R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2*R5(R3+R4))))(R1-R6))/R5
voila normalement la c'est bon
Y'a au moins 2 erreur vers la fin:
R2*R5(R3+R4) au lieu de R2+R3+R4+R5
et
(R1-R6) au lieu de (R1+R6)
Mais c'est pas grave. J'arrivais à lire ni à suivre une logique... Désolé.
R équivalente=R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2*R5(R3+R4)))
devient R équivalente=R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2+R5(R3+R4)))
donc juste le + qui change
et I1 devient
I1=(U-(R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2+R5(R3+R4))))(R1-R6))/R5
je reprend juste ce qui est faux
I1=(U-I(R1+R6))/R5 je change le "-" en "+"
ensuite il manquait U dans U=RI
I=U/(R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2+R5(R3+R4))))
donc I1=(U-(U/(R1+R6+((R5R2+R5(R3+R4)+R2(R3+R4))/(R2+R5(R3+R4)))))(R1+R6))/R5
et voila j'ai votre résultat
par contre pour R équivalente je l'ai refait et sa me parait plus simple comme sa
maintenant je re-récapitule:
R équivalente (dans la branche ou il y a R3 et R4)=(R3+R4)
1/R équivalente (des trois branches en dérivation)= 1/R2 + 1/(R3+R4) + 1/R5
R équivalente (des trois branches en dérivation)=((R2R5(R3+R4))/(R2(R3+R4)+R5(R3+R4)+R2R5)),
donc R équivalente (pour toute les résistances)= R1+R6+((R2R5(R3+R4))/(R2(R3+R4)+R5(R3+R4)+R2R5))
U5=R5*I1
je nomme U1 la tension passant par R1 et U6 celle de R6
enfin U' celle passant dans les trois branche (U'=U2=U3/4=U5)
U=U1+U'+U6 (loi des maille)
U'=U-U1-U6
U5=U'
U5=U-U1-U6
I1=U5/R5
I1=(U-U1-U6)/R5
U=RI
U1=R1*I
U6=R6*I
I1=(U-I(R1+R6))/R5
U=R équivalente*I
R équivalente=U/(R1+R6+((R2R5(R3+R4))/(R2(R3+R4)+R5(R3+R4)+R2R5)))
I1=(U-(U/(R1+R6+((R2R5(R3+R4))/(R2(R3+R4)+R5(R3+R4)+R2R5))))(R1+R6))/R5
voila je pense que la c'est bon

 R/(R1+R+R6)
R/(R1+R+R6)



