Inscription / Connexion Nouveau Sujet
Triangulation laser
Bonjour,
Pour faire des releves de distance sur le terrain, on utilise un faisceau laser avec lequel on vise le centre d'un panneau indicateur a partir de 2 positions A et B situées de part et d'autre d'une route rectiligne.
La droite joignant A et B est perpendiculaire à l'axe de la route.
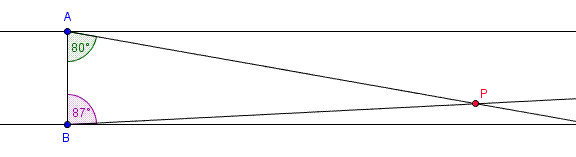
Les angles interieurs au triangle forme par les 2 rayons lasers et la droite (AB) ont pour valeur 80° en 1 et 87° en B.
a) Faire un schéma de la situation
b) A quelle distance du point B se trouve le panneau, sachant que la distance Ab vaut 0,6 m ?
En fait, le probleme, c'est que je n'arrive pas à m'imaginer "la scene". Donc, j'arrive pas a faire le schéma... et donc, j'arrive pas a faire la 2nd question.
Pouvez vous m'expliquez svp ? merci d'avance 
Aicha
Edit Coll : police des caractères : suppression du souligné
Es-tu sûre de la valeur de la largeur de la route ? Ce n'est pas très large, 60 centimètres, pour une route ! Même pas une piste cyclable...
J'appelle H le pied de la hauteur issue de P dans le triangle APB
D'où : deux triangles rectangles APH et PHB
J'appelle x la distance BH
J'écris la distance HP (inconnue) en fonction de x dans le triangle BHP et en fonction de (0,6 - x) dans le triangle APH
Ceci me permet de connaître une expression x = ...
Ensuite il n'y a plus qu'à écrire dans le triangle PHB une relation entre BP que l'on cherche et HB = x que l'on vient de déterminer.
Essaye cette méthode !
Avec AB = 0,6 m je trouve BP 
2,63 m (sauf erreur ! )
Je ne savais pas que tu connaissais ces relations pour les triangles quelconques. Mais aucun doute que c'est beaucoup plus rapide que ce que je te proposais.
Sachant que l'angle a pour mesure 180° - (80° + 87°) = 13°
On écrit :
AB / sin(13°) = BP / sin(80°)
et donc
BP = AB 
sin(80°) / sin(13°) = 0,6 sin(80°) / sin(13°) 2,63 m
Bravo !
Annuler
connectez vous