Inscription / Connexion Nouveau Sujet
Travaille et puissance..
Bonsoir ,bon voilà on viens juste d'entamer ce chap et bah je n'ai pas bien compris le cours, Je me suis dis peut être en m'exerçant je comprendrai . Je vous prie de m'assister sur cet exo. Merci d'avance.
Exercice :
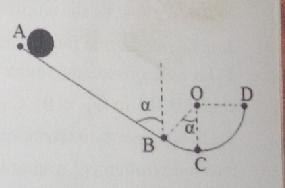
Une piste verticale est formée d'une portion rectiligne AB=1,2m ,incliné d'un angle 
=45° par rapport à la verticale d'une partie circulaire BCD raccordée en B à AB ,de rayon r=25cm.Un solide S supposé ponctuel de masse m=0,2kg est abandonné en A sans vitesse initiale.
1)En supposant les frottement négligeable, Calculer la vitesse du solide au point B ,C et D.
2)En réalité les frottements ne sont pas négligeable sur la portion BCD et la nouvelle vitesse en D est VD=3m/s .
a)Calculer la vitesse réelle VC du solide.
b)En déduire la valeur de la force de frottement supposée constante qui s'exerce sur le solide
Voilà ce que j'ai fais :
1) la vitesse au point B
D'après le théorème de l'énergie cinetique:
Ec=
Fext.
=>EcB-EcA=W(P)+W(R)
=>1/2.m.VB²=P.h +0 d'où h=AB.cos et VA=0
=>VB²=2.p*AB.cos45°/m
=>VB²=16,95 =>VB=4,11m/s
Bonjour,
Question 1 :
Ton calcul est exact.
Pour obtenir la vitesse en C tu peux appliquer le théorème de l'énergie cinétique entre B et C, puis l'appliquer à nouveau entre C et D pour obtenir la vitesse au point D.
OK Merci.
Calculons la vitesse au point C
EcC-EcD=Fext.
=>1/2mVc²-1/2mVb²=W(p)+W(R).
=>1/2mVc²=P.H+1/2mVb² d'où h=r.cos45
Vc²=2*m.g*r.cos45+1/2mVb²/m.
Vc²=20,4 =>Vc=4,51m/s.
Calculons la vitesse au point D.
EcD-EcC=W(p)+W(R)
1/2mVD²-1/2mVC²=-P.h d'où h=r.cos45
=>Vd²=-2*m.g*r.cos45+1/2mVc²/m
Vd²=16,9=> Vd=4,11m/s
La méthode est bonne. mais ....
Vc²=2*m.g*r.cos45+1/2mVb²/m.
La dénivellation (différence de niveau) entre B et C n'est pas égale à r*cos(45°)
Vd²=-2*m.g*r.cos45+1/2mVc²/m
De même la dénivellation entre C et D n'est pas non plus égale à r*cos(45°)
OK je reprends l'application numérique.
La vitesse au point C.
Vc²=2mg.r(1-cos45)+0,5*0,2*16,95/m
Vc²=0,29+1,69/0,2=1,98/0,2=0,7/0,2
Vc²=9,9 => Vc=3,1m/s.
La vitesse au point D.
Vd²=-2_mg.r(1-cos45)+0,5mVc²/m
Vd²=-0,29+0,99/0,2=0,7/0,2=3,5
Vd=1,8m/s
Tu avais trouvé ( et moi aussi) :
VB = 4,12 m/s
Je m'attends, bien sûr, (puisque C est au dessous de B) à trouver VC > VB
mais tu trouves VC = 3,1 m/s
J'en déduis que tu as du faire une erreur.
VB, g, r et sont connus.
Je te laisse le soin de faire l'application numérique.
La vitesse au point D.
Vd²=-2_mg.r(1-cos45)+0,5mVc²/m
Non
Entre C et D la dénivellation que tu as utilisée est fausse.
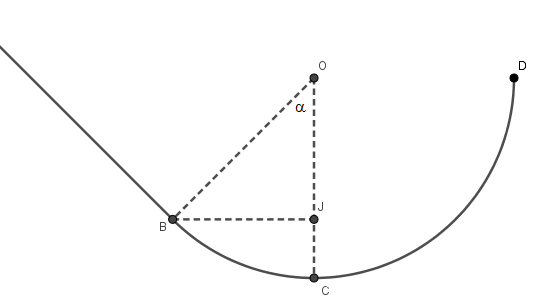
Voir mon schéma du 17-01-19 à 17:35
OK pour la valeur numérique de VC
L'expression que tu as trouvée pour VD est fausse.
Elle restera fausse tant que tu n'auras pas d'abord répondu à la question :
Quelle est la dénivellation entre les points C et D ?
Voir la figure. ( 17-01-19 à 17:35)
Je l'ai faite pour que tu t'en serves !!!
Si on trace le [OD] et [CD] on aura un triangle rectangle en O . est-ce dans ce triangle rectangle pourrais je trouvé l'expression demandé ?
Si on trace OD on constate que ces deux points sont au même niveau.
La dénivellation cherchée ( entre C et D ) est donc la même qu'entre C et O
Que vaut-elle ?
Tracer CD est parfaitement inutile.
Merci de noter
par V'(C) la nouvelle valeur de la vitesse en C
par V'(D) la nouvelle valeur de la vitesse en D
Sinon les confusions vont apparaître et on ne saura jamais de quoi on parle.
Un minimum de rigueur est indispensable en sciences.
J'ai beau chercher je n'arrive pas à comprendre pour quelle raison tu écris :
Vc²=VD²+2gr
Si ru as des arguments pour écrire cela montre les !
Et non je n'ai pas d'argument concret, bon En fait j'ai juste utilisé l'expression d'au départ :
1/2mVd²-1/2mVc²=-mgr
Donc 1/2mVd²'-1/2mVc²'=-mgr
Je croyais que cette expression pourrait servir à déterminé la Vc'.
Comment dois-je m'y prendre ?
En fait j'ai juste utilisé l'expression ....
Je croyais que ....
On ne fait pas de la physique en utilisant des "formules" au petit bonheur et "en croyant que ..."
Tu peux commencer par calculer en D la perte d'énergie cinétique
(Ec) due aux frottements.
Pour cela tu calcules :
Ec(D) : Energie cinétique en D en absence de frottements.
E'c(D) : Energie cinétique en D en présence de frottements.
(Ec) = Ec(D) - E'c(D) : perte d'énergie cinétique due aux frottementsOn ne fait pas de la physique en utilisant des "formules" au petit bonheur et "en croyant que ..."
😅 désolé
Ec(D)=1/2mVD²=0,5*0,25*13,4=1,67J
Ec'(D)=1/2mVD'²=0,5*0,25*9=1,12 J.
Ec=1,67-1,12=0,55 =>Ec=0,55J
Revois tes applications numériques.
m = 0,2 kg et non 0,25 m !
Merci de respecter les notations et ne pas noter Ec ce qui est (Ec)
Ah oui oui je n'ai pas bien fait attention :
Ec(D)=0,5*0,2*13,4=1,34J
Ec'=0,5*0,2*9=0,9J
(Ec)=1,34-0,9=0,44J
OK
Donc, à cause des frottements le solide S a perdu 0,44J sur le trajet BD
Tu peux à l'aide d'un raisonnement extrêmement simple en déduire quelle a été sa perte d'énergie cinétique sur le trajet BC
Revoir pour t'aider mon schéma du 17-01-19 à 17:35
Le trajet BC a une longueur égale au tiers du trajet BD
La perte d'énergie cinétique sur le trajet BC est égale au tiers de la perte d'énergie cinétique sur le trajet BD
Entre B et C cette perte d'énergie cinétique est donc égale à 0,44/3 = 0,147J
Tu peux maintenant calculer la nouvelle valeur de l'énergie cinétique en C à partir de son ancienne valeur et de la perte de 0,147J
Connaissant la nouvelle valeur de l'énergie cinétique en C il sera facile de calculer la nouvelle valeur de la vitesse en C
Enfin en appliquant le théorème de l'énergie cinétique entre B et C tu pourra répondre à la question 2b)
Annuler
connectez vous