Inscription / Connexion Nouveau Sujet
Travaille et puissance 2
Bonsoir,s'ils vous plait aidez moi à faire cette exo.
Exercice :
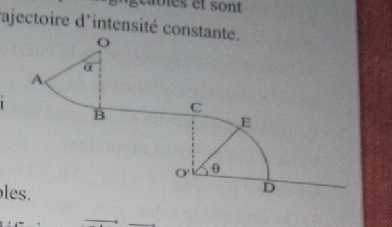
Un solide de masse m=3kg part de A sans vitesse initiale et glisse sur un début de piste formé de 3 parties comme l'indique la figure ci-dessous.
La partie AB représente une un sixième de circonférence verticale d'un cercle de rayon R=5cm et de centre O.
BC est une partie rectiligne horizontale de longueur L=R.
CD est un quart du circonférence verticale de cercle de rayon R et de centre O.
1)Lors du premier essaie sur la piste ABC les frottements sont négliges .
Avec quelle vitesse Vb et Vc ,le solide passe-t-il en B et en C?
2)Au cours du deuxième essaie les frottements ne sont pas négligeables et son équivalent à une force unique f tangente à la trajectoire d'intensité constante.
a)Exprimer VB en fonction de m,f R, g et 
.
b)Exprimer Vc en fonction de m ,f ,R et VB.
c)Calculer l'intensité de la force de frottement si le solide arrive C avec une vitesse nulle .
3)Le solide arrive en C avec une vitesse nulle.Il aborde la partie CD avec frottements négligeables.
a)Le solide passe en un point E de la piste CD défini par (vec O'D ,vec OE)=
,O'D étant porter par l'horizontale. Exprimer sa vitesse VE en fonction de g ,R et .
b) Le solide quitte la piste E avec une vitesse VE=6m/s .Calculer la valeur de l'angle.
c)A quelle vitesse le solide atterit-il sur la piste de réception en un point X.
On donne g=10N/kg
bonjour,
1) si les frottements sont négligé, l'énergie mécanique se conserve
donc Em(A) = Em(B) = Em(C)
Oui je vois mais je me demande si je pourrais utilisé la théorème de l'inergie pour pouvoir : déterminer la vitesse VB et VC.
D'après le théorème :
EcB-EcA=W(P)+W(R)
=>1/2mVB²=P.h=>VB²=2*P.h/m=>VB²=2*m.g*h/m
comment trouver la hauteur?
oui, tu peux, tu trouves le meme résultat puisque c'est equivalent dans le cas où il n'y a pas de frottement: W(P) = -
Epp et W(R) = 0
pour trouver h il faut passer par le point I projection orthogonale de A sur OB
on connait OA, OB et OI se calcule en fct deOA et
enfin h = OB-OI
OK ,alors h=R-R.cos)=R(1-cos.
VB²=2mg.R(1-cos)/m
_VB²=2*3*10*0,05(1-cos)/3
VB²=3(1-cos)/3
VB²=1-cos=>VB=
1-cos
La vitesse au point C.
EcC-EcB=W(p)+W(R)
1/2mVc²-1/2mVb²=m.g.h or h=r
Vc²=Vb²+2.g.r=0,5+2*10*0,05=1,5.
=>Vc=1,2m/s
Ah Oui oui ,j'ai failli oublié cet régle
Vitesse au point C
W(p)=0.
1/2mVc²=1/2mVb²
Vc²=Vb²=0,5 =>Vc=0,7m/s
Pour la question 2.
2)Exprimé Vb=f(m, R, g ,)
Je ne vois pas trop comment procédé surtout comment entré f dans l'expression ?
Tu écris le même théorème que pour le 1) en ajoutant ici le travail de f
W(f)= -f x longueur de l'arc AB
Puisque f est constante, toujours tangente a la trajectoire et opposée au mouvement
/3
Annuler
connectez vous